Design of high energy storage ferroelectric materials by phase-field simulations
Abstract
The improvement in energy storage performance of ferroelectric (FE) materials requires both high electric breakdown strength and significant polarization change. The phase-field method can couple the multi-physics-field factors. It can realize the simulation of electric breakdown and polarization evolution. It is widely used to reveal the modification mechanism and guide experimental design. Starting with the models of electric breakdown and polarization evolution, this work reviews the latest theoretical progress on FE materials with high energy storage performance. Firstly, the enhancement mechanisms of electric breakdown strength are analyzed. Subsequently, the improvement strategies at domain scales are analyzed. Finally, this review summarizes and looks ahead to the development of theoretical models, such as machine learning models.
Keywords
INTRODUCTION
In the current rapid development of electronic technology, the efficient storage and utilization of energy has become the focus in numerous research fields. Batteries used in electric vehicles, portable electronics, and distributed energy storage systems have high energy density and mature technology but suffer from slow charge-discharge speed and limited cycle life. Electrochemical capacitors, including supercapacitors, applied in consumer electronics, transportation, and industrial equipment, feature high power density, long cycle life, and high charge-discharge efficiency, yet possess high self-discharge rate. Among them, high-performance dielectric capacitors play an important role in high-power pulse systems, miniaturized electronic devices, and new energy vehicles. Dielectric capacitors possess advantages such as high power density, high charge-discharge rate, and easy integration. However, compared with batteries and electrochemical capacitors, the energy storage density of dielectric capacitors needs to be further improved[1-3].
The modification of dielectric materials is a key factor in improving the energy storage performance of capacitors. Compared with traditional ceramic dielectrics (such as MgO, Al2O3) and organic thin film dielectrics, such as polypropylene (with a dielectric permittivity of about 10), ferroelectric (FE) materials possess an extremely high dielectric permittivity (about 103). The high dielectric permittivity stems from the spontaneous polarization characteristic of FE materials. That is, under zero external electric field, there is an ordered arrangement of dipoles inside the crystal, resulting in polarization. Spontaneous polarization appears as domains at the mesoscopic scale, while the entire material remains electrically neutral. The formation of domains also implies that the dielectric response of FE materials has a hysteresis characteristic, which is manifested as a nonlinear hysteresis loop. Based on the hysteresis loop, we can calculate the recoverable energy storage density (Wrec) of FE materials during charge-discharge process:
Electric breakdown refers to the phenomenon in which the insulation of a dielectric/FE material suddenly disappears and the current rapidly increases under the influence of external electric field. Intrinsic breakdown is usually related to electron transitions under a high electric field. Extrinsic breakdown is associated with the defects, phase interfaces, and grain boundaries of FE materials. To obtain a higher Eb, numerous experimental modification strategies are employed in the preparation of FE energy storage materials, including nanocomposites[4-9], core-shell structures[10-13], multi-layer ceramic capacitors (MLCC), and thin films[14,15]. In addition, recent studies usually adopt element doping to obtain relaxor ferroelectrics (RFE), and select antiferroelectric (AFE) materials and strain engineering to obtain a larger ΔP. RFE usually has a diffuse dielectric-temperature peak and smaller domain size, corresponding to extremely small Pr and loss energy density (Wloss). Due to the antiparallel polarization configuration, AFE materials exhibit the response characteristics of linear dielectrics under low electric field. Only when the external electric field is greater than the phase transition electric field (EAF) will an obvious hysteresis appear. Overall, the different configurations of FE polarization can change the macroscopic dielectric response and determine the energy storage performance.
However, experiments have limited capabilities in characterizing the electric breakdown path and the polarization evolution process. The latest research shows that the electrical tree propagation rate in the transparent dielectric polymethyl methacrylate (PMMA) is on the order of 106 to 107 m/s[16]. The characterization of electric breakdown in FE materials will be even more difficult. Although piezoresponse force microscopy can in-situ characterize the switching of FE domains under an external electric field, it is still challenging to characterize the switching dynamics of nanodomains or even dipoles. As a mesoscopic simulation method, the phase-field methods can introduce multiple order parameters such as polarization and breakdown phases based on FE materials and couple multi-physics-field factors such as temperature, electric field, and strain field. It has been widely applied to research on the mesoscopic dynamic mechanism and macroscopic physical property response of FE materials.
This paper mainly reviews the modification strategies for FE energy storage materials. Firstly, it introduces the current development status of the phase-field models for electric breakdown and polarization evolution. Besides, based on phase-field simulations, the enhancement mechanisms of Eb and ΔP are revealed [Figure 1]. In addition, we review some reports on capacitors with high energy storage performance and present the values of ΔP and Eb, as shown in Figure 2. Finally, the development of multi-scale phase-field models and the combination of machine learning with phase-field simulations for the design of high-performance energy storage materials are prospected.
Figure 1. Phase-field simulations for designing FE materials with high energy storage performance. Domain structure evolution simulation to enhance polarization change ΔP. Element doping. This figure is quoted with the permission from Shu et al.[17], copyright 2024, AAAS. Topological domain. This figure is quoted with the permission from Qian et al.[18], copyright 2023, John Wiley and Sons. Strain engineering. AFE. This figure is quoted with permission from Liu et al.[19], copyright 2020, Elsevier. Electric breakdown evolution simulation to enhance breakdown field strength Eb. Nanocomposite. This figure is quoted with permission from Sun et al.[9] ,copyright 2022, Elsevier. Polycrystalline. This figure is quoted with permission from Wu et al.[20], copyright 2020, AIP Publishing. Core-shell structure. This figure is quoted with permission from Bi et al.[21], copyright 2018, Elsevier. Multi-layer. This figure is quoted with permission from Chen et al.[22], copyright 2023, John Wiley and Sons. FE: Ferroelectric; AFE: antiferroelectric.
Figure 2. Comparisons of polarization change and electric breakdown strength of thin film energy storage materials, including Fe-doped (Na0.5Bi0.5)TiO3[23], Bi3.25La0.75Ti3O12[24], (Pb0.92La0.08)(Zr0.52Ti0.48)O3[25], 0.94(Bi0.5,Na0.5)TiO3-0.06BaTiO3[9], Mn-doped
PHASE-FIELD MODELS
Theoretical fundamentals of phase-field simulations
The evolution process of polarization switching can be obtained by solving Time Dependent Ginzburg Landau (TDGL) equation[36,37],
where Pi (r, t) is polarization, L is the kinetic coefficient, and F is the total free energy of the system, which is expressed as
where V is the system volume. The Landau free energy density fLand can be calculated by
where P1, P2, P3 are polarization components. α1, α11, α12, α111, α112 and α123 are Landau coefficients. The elastic energy density can be expressed as[38]
where Cijkl is the elastic stiffness tensor, and ε and ε0 are the total local strain and the eigenstrain, respectively. The eigenstrain is defined as follows
where Qijkl is the electrostrictive coefficient of the corresponding crystal. To solve the equilibrium heterogeneous strain field δεij, a set of displacements ui(x) have been introduced,
the mechanical equilibrium condition is given by
where σij is the elastic stress. The gradient energy density can be expressed as
where i = 1, 2, 3, and gijkl is the gradient energy coefficient. The electrostatic energy density is given as follows[36,39]
where fdipole is dipole-dipole interaction energy density due to the inhomogeneous distribution of polarization. fappel is an additional electrical energy density caused by the external electric field,
where Ei denotes the inhomogeneous electric field due to dipole-dipole interactions. It is obtained by solving the electrostatic equilibrium equation given by
where Di is the electrical displacement represented by
where κ0 is the dielectric permittivity of vacuum and κij the relative dielectric permittivity. In this part, the spectral iterative perturbation method is also employed to solve Poisson’s equation. When an external electric field is applied in the global ith direction, an additional contribution fappel should be taken into consideration,
where
Phase-field model of electric breakdown
In the phase-field model of electric breakdown, electrical trees are analogized to mechanical fractures[40]. The scalar field η (r, t) is adopted to represent the electrical trees in solid dielectrics[41]. η = 1 represents the breakdown phase, and dielectric permittivity of the damaged region is assumed to be large enough. η = 0 indicates the intact state. Fb is the total free energy of the two-phase system that can be written as[42-44],
where κ is the gradient energy coefficient. fchem is the chemical free energy density function that has two global energy minima at 0 and 1,
where D0 is a positive coefficient defining the energy barrier of the phase separation. The electric energy density coupled with the break phase is calculated as
where κ0 is the vacuum dielectric permittivity, κij (η) can be defined as a function of the relative dielectric permittivity of the breakdown phase (κb), the FE phase (κr), and the polymer matrix (κm), respectively.
Phase-field model of thin films
The mechanical boundary condition for the film is such that its top surface is stress-free,
where hf is the film thickness, while the bottom surface is coherently constrained.
The electrical boundary conditions also need to be adjusted accordingly. Besides satisfying the electrostatic equilibrium equation Equation (11), for the close-circuit boundary conditions,
Electrical potential ϕ is related to Ei through Ei = -ϕi. An additional surface depolarization energy (fdepol) needs to be introduced into the electrostatic energy term,
Where Eidepol is the depolarization field.
Phase-field model of RFE materials
In the RFE phase-field model, TDGL equation should incorporate the thermal noise term[45-47],
Where ξi (r, t) represents the effect of thermal noise, which is a Gaussian random fluctuation.
For the polar nanoregions (PNRs) generated by element doping, the Landau free energy term is usually introduced in the form of a second phase. To simplify the treatment of the elastic energy term, we usually assume that the PNRs have the same elastic constants and electrostrictive coefficients as those of the matrix. The PNRs possess different Curie temperatures (TC) and spontaneous polarization magnitude from the FE matrix phase, and exhibit the characteristics of RFE in the dielectric-temperature spectra. In addition, for point defects such as oxygen vacancies or defect dipoles caused by element doping, the random field effect also needs to be considered[48-53]. The electrostatic energy term requires an additional local energy term generated by the random field effect,
where Eilocal is the local electric field along the ith direction caused by element doping.
Phase-field model of AFE materials
AFE possesses an antiparallel spontaneous polarization configuration, and Pr is zero without external electric field. Based on the characteristics of AFE phases, researchers have established different phase-field models to explain AFE materials. For the mixed phase of AFE and FE, an AFE phase order parameter Ai can be additionally introduced, and the Landau free energy can be expressed as[54,55],
Due to the interaction between AFE phase and FE phase, a coupling energy term needs to be introduced,
This model can simulate the transformation from AFE to FE under the external electric field. For the precise description of the antiparallel polarization of AFE, the next-nearest neighbor interaction model can be adopted. The gradient energy density can be expressed as[19,56,57],
Where θi is the oxygen tilt. β11 and β12 are the positive constants, which describe polar-polar interactions. γ11 and γ12 are the positive constants, which describe the coupling between oxygen tilt and polarizations. φ11 and φ12 are the positive constants of high-order gradient energy describing next-nearest-neighbor interaction between polarizations, which can drive the phase transition from AFE to FE. This model can not only simulate the antiparallel polarization configuration, but also regulate the transition from the commensurate phase to the incommensurate phase by tuning tilting angle of the oxygen octahedron.
MODEL-GUIDED DESIGN OF ELECTRIC BREAKDOWN STRENGTH ENHANCEMENT
Linear dielectrics and polymers possess high Eb and low dielectric permittivity, while FE ceramics have low Eb and high dielectric permittivity. The introduction of FE nanofillers into the matrix with high Eb is widely regarded as a design strategy for the coordinated enhancement of Eb and ΔP. Recent research indicates that the mesoscopic physical process of dielectric breakdown is approximately the nucleation and growth of electrical trees under a high electric field. The composite structure is heterogeneous, resulting in an inhomogeneous distribution of electric field strength. The nucleation of electric breakdown phase is likely to occur at interfaces with a low Eb. The electric breakdown path evolves in the form of an electrical tree driven by the local high electric field. When the electric breakdown path penetrates the material, it is considered to have completely failed. The mechanism by which the FE composite structure improves the Eb is that the introduction of the high dielectric permittivity phase can tune the local electric field distribution. However, the evolution process of electric breakdown is difficult to characterize, and the breakdown dynamics mechanism of complex structures still needs to be further explored. Therefore, it is very important to guide the design of composite structures via phase-field simulations.
FE nanofiller composite structures
The most common design concept for composite structures is to use polymers as the matrix and dope with FE nanoparticles, nanofibers, nanosheets, etc.[6,58]. The electric field distribution of the polymer-FE nanofiller determines the evolution of the electric breakdown paths. In the SrTiO3 (STO)-polyethylene composite structure, when the volume fraction of STO particles remains unchanged at 12%, the aggregated particles have higher dielectric permittivity and dielectric loss than the dispersed ones. There is a higher electric field strength among STO particles[59]. A similar electric field distribution has also been reported in BaTiO3 (BTO)-polymer composite materials[5,6]. Shen et al. investigate how nanofillers with different shapes and sizes regulate the electric field of polymers[43]. Nanofibers parallel to the direction of the electric field can weaken the depolarization effect due to their high aspect ratio, which is beneficial for increasing the effective dielectric permittivity. Nanosheets that are vertical to the direction of the electric field can make the electric field distribution more uniform through their special two-dimensional morphology and orientation, effectively reducing the local electric field strength and thus improving Eb [Figure 3A].
Figure 3. Phase-field simulations of FE nanocomposite. (A) Electric field distribution of FE nanofibers in a polymer matrix parallel and vertical to the external electric field[43]; (B) Electric breakdown evolution path and Eb of BTO nanoparticle and nanofiber. This figure is quoted with permission from Shen et al.[42], copyright 2018, John Wiley and Sons. FE: Ferroelectric; BTO: BaTiO3.
In the Ba0.67Sr0.33TiO3 (BST) - P(VDF-TrFE-CFE) nanofiber composite, when the nanofibers are parallel to the external electric field (E = 50 MV/m), their tips possess an extremely high electric field strength (approximately 120 MV/m). When the nanofibers are randomly arranged, the electric field distribution becomes more uniform[60]. Besides the factors of shape and orientation, the density of nanofillers also has a significant impact on the electric field distribution. In the BaZr0.2Ti0.8O3 (BZT)-polyvinylidene fluoride (PVDF) composite, as the volume fraction of BZT increases from 2.5% to 7.5%, the breakdown field strength first increases and then decreases[9]. Simulation results show that the low-density BZT phase can reduce the local electric field strength. However, an excessively high density BZT will lead to the concentration of the electric field at adjacent tips. Therefore, the concentration, shape and distribution of nanofillers can all affect the electric field distribution and, in turn, change the Eb[4,42,43,61,62].
Based on the theoretical basis of the electric field distribution regulated by the nanofiller composite structure, phase-field model has been widely applied to the simulation of electric breakdown paths[63-65]. Shen et al. adopt phase-field simulations to study the influence of the PVDF-BTO composite structure on the electric breakdown path[42,66]. The high electric field strength at the tips promotes the breakdown phase to avoid the nanoparticles. The parallel nanosheets make the electric field uniform and hinder the evolution of electrical trees. The vertical nanosheets (volume = 10%) increase the Eb from 230 to 310 kV/mm, as shown in Figure 3B. In general, high electric field promotes the evolution of electric breakdown. When introducing the nano FE phase, it is necessary to balance the electric field distribution as much as possible to avoid high local electric field at the interface between two phases. In this way, Eb of the composite structure can be improved. Wang et al. utilize phase-field methods to study the effect of the angle between nanofibers and the electric field on Eb[67]. As the angle rises from 0° to 90°, Eb of the composite gradually increases. With the increase in angle, distortion of the electric field decreases. During the breakdown evolution process, nanofibers with a larger inclination angle can make the breakdown path more tortuous and consume more energy. An increasing number of composite structure designs with FE nanosheets are being used to improve Eb.
Bao et al. compared the improvement of Eb by electrically neutral and negatively charged Ca2Nb3O10 (CNO) nanosheets[61]. During the process in which the charge carriers move to the anode, when contacting negatively charged CNO nanosheets, electrons will be decelerated or blocked. Phase-field simulations show that the kinetic decay inhibits the development of breakdown path, making it necessary for a higher electric field to form the breakdown phase when passing through the nanosheets, and ultimately improving Eb of the nanocomposite. Dong et al. introduce the Bi0.5Na0.5TiO3 (BNT) RFE with endotaxial nanostructures (ENs)[68]. The lattice mismatch, formed by nanofillers with the matrix, generates local potential fluctuations, increases electron scattering and reduces electrical conductivity. Phase-field simulations show that ENs delay the development of electric breakdown paths. Under the same electric field, the fraction of the breakdown phase containing ENs is much lower than that of the ceramic without ENs.
Multi-layer composite structures
Besides the FE nanofiller composite structures, phase-field simulations have also been used to reveal the electric breakdown dynamics of organic-inorganic multi-layer structures. The research team finds that the Sm-BiFeO3 (BFO)-BTO FE layer added to the PVDF matrix exhibits a relatively small electric field strength under the external electric field. The FE buffer layer reduces the driving force at the tips of electrical trees, hinders the expansion of electrical trees, and increases Eb from 550 to 770 MV/m[69]. Chen et al. fill the PbZrO3 (PZO) single-crystal film into the PVDF matrix[22]. The introduction of a PZO AFE layer (0.2 μm) significantly increased Eb from 500 to 695 MV/m. As the thickness of PZO increases, Eb of the composite structure first increases and then decreases. Phase-field simulation results indicate that the PZO single-crystal film prolongs the expansion path of electric breakdown, as shown in Figure 4. Cai et al. use phase-field methods to simulate the multi-layer structure with Al2O3 and SiO2-doped BTO ceramics (BTAS) as the mid-layer[70].
Figure 4. Phase-field simulation of breakdown path evolution in multi-layer structures. Electric breakdown path in pure PVDF and PVDF-PZO-PVDF with different thicknesses of mid-layer. This figure is quoted with permission from Chen et al.[22], copyright 2023, John Wiley and Sons. PVDF: Polyvinylidene fluoride; PZO: PbZrO3.
Research shows that the BTAS ceramic layer has a higher Eb. The continuous multi-layer structure can prompt the electric breakdown path to branch, significantly increasing energy dissipation. The key to the design of multi-layer composite structures lies in finding suitable buffer layer materials, appropriate thickness ratios, and optimal stacking sequences. On the one hand, an overly thin multi-layer structure may introduce a high density of defects at the interfaces. On the other hand, if the FE layer is too thick, the overall Eb of the composite structure will be reduced. Therefore, phase-field simulations can effectively guide the design of multi-layer structures. Li et al. conduct a simulation of the electric field distribution for the multi-layer P(VDF-HFP)/BTO-PMMA-P(VDF-HFP)/BTO[62]. The introduction of BTO particles reduces the electric field strength, enabling the PMMA layer with a high Eb to withstand a higher voltage and thus enhancing the Eb. Recently, it has been reported in studies that, compared with the pure polyetherimide (PEI) samples, in the sandwich structure of Bi0.5(Na0.84K0.16)0.5TiO3 (BNKT)-BST-based nanoparticles, the developing electrical branches in the monolayer 0.75 vol.% BNKT-BST/PEI nanocomposite are blocked by BNKT-BST, thus increasing the evolutionary branching[71]. Jiang et al. investigate the energy storage performance of the PVDF-BZT-based nanocomposite structure with a gradient structure. The gradient distribution of the BZT phase enables it to withstand a higher electric field load in the polymer matrix[72], maximizing the polarization intensity of the material without sacrificing the electric field strength.
Core-shell structures
To solve the problem of electric field strength distortion at the interface between FE ceramics and the matrix phase, the core-shell structure with passivation layer coating FE ceramics has also been widely used in the design of dielectrics with high energy storage performance. Wu et al. analyze the influence of the shell layer thickness factor on the electric field distribution, and the simulation results described the shell layer thickness by using the shell layer volume fraction[12]. As the volume fraction increases from 5% to 20%, the non-uniform electric field of shell is alleviated, the local maximum electric field strength decreases from 2,500 to 1,000 V/μm, and Eb is improved [Figure 5A]. The essence of increasing the shell layer thickness is to achieve a smoother transition at the phase interface. This alleviates the distortion of dielectric permittivity at the core - shell interfaces and leads to a more uniform distribution of the electric field strength. Bi et al. used the electric breakdown phase-field model to study the BTO@SiO2-PVDF core-shell structure[21]. In the BTO-PVDF structure without the interfacial SiO2 layer added, the electrical trees will directly penetrate the BTO particles which have a lower Eb. After introducing the interfacial shell layer, since SiO2 has an extremely high Eb, the propagation of the electrical trees needs to overcome a higher barrier. Only when SiO2 is completely broken down will the electrical trees further propagate [Figure 5B].
Figure 5. Phase-field simulation of breakdown path evolution and electric field distribution in core-shell structures. (A) Electric field distribution with different thickness of shell. This figure is quoted with permission from Wu et al.[12], copyright 2015, John Wiley and Sons; (B) Breakdown path with core-shell BTO@SiO2 nanofillers and uncoated BTO nanofillers. This figure is quoted with permission from Bi et al.[21], copyright 2018, Elsevier; (C) Grain structures, domain structures of the unpoled state and electric field distributions of the poled state under an applied electric field of 400 MV/m, respectively, of the PZT films. This figure is quoted with permission from Peddigari et al.[10] copyright 2023, John Wiley and Sons. BTO: BaTiO3; PZT: PbZr1-xTixO3.
Zhao et al. also use SiO2 with a high Eb as the shell layer in 0.87BTO-0.13Bi(Zn2/3(Nb0.85Ta0.15)1/3)O3 MLCC[73]. Simulation results show that the core-shell structure increases the Eb by nearly 100%. Recently, the crystal-amorphous core-shell structure has also been applied to significantly improve the Eb of PbZr1-xTixO3 (PZT) thick films[10]. A mechanical energy-induced nanograin engineering approach has been employed to form PZT@amorphous core-shell structure. Under the action of mechanical energy, PZT powder is deposited into nanocrystals and coated by the amorphous phase to form a core-shell structure. Phase-field simulation results show that the amorphous shell layer with a higher Eb bears a higher electric field strength (about
Electric breakdown mechanisms of FE polycrystalline
Serious geometric distortions, defects and inclusions exist at the grain boundaries of FE energy storage ceramics. Therefore, there are significant differences in electrical properties compared with FE grains. Studying the relationships between factors such as grain size and grain boundary properties is important for guiding the design of materials with high Eb[74-80]. Cai et al. assume the grain boundaries as linear dielectric layers and establish an electric breakdown phase-field model for BTO polycrystalline[81]. The results of phase-field simulations show that in large grains, the grain boundaries that are vertical to the external electric field have a higher strength. As the grain size decreases from 125 to 50 nm, the electric field distribution at the grain boundaries becomes more uniform. Since Eb at the grain boundaries is higher than that inside grains, the electric breakdown path is blocked when it encounters the grain boundaries. When the local electrostatic energy is large enough, the breakdown path penetrates the grain boundaries. Therefore, it is generally believed that Eb increases as the grain size decreases [Figure 6A]. After FE ceramics are doped with elements, the grain size tends to decrease, which is also regarded as an effective strategy for improving Eb[20,78,82].
Figure 6. Grain size and grain boundary effect of Eb. (A) P-E loops and Eb of BTO with different grain sizes. This figure is quoted with permission from Cai et al.[81], copyright 2018, John Wiley and Sons; (B) Electric field distribution and (C) breakdown path at the critical breakdown state of samples KNBNTF and KBT. These figures are quoted with permission from Li et al.[83], copyright 2024, John Wiley and Sons. BTO: BaTiO3; KNBNTF: KBT-Na0.5Bi0.5ZrO3-Bi0.85Nd0.15FeO3; KBT: K0.5Bi0.5TiO3.
Research teams have put forward more diverse polycrystalline breakdown mechanisms. The element doping design for K0.5Bi0.5TiO3 (KBT)-based materials can suppress the segregation phenomenon of electric field strength near the grain boundaries, as shown in Figure 6B[83]. After doping modification, 0.83KBT-
The pores and distribution of FE polycrystalline ceramics also have a significant impact on the electric breakdown performance[84]. This research shows that the reason why FE ceramic grain boundaries, which have a low dielectric permittivity, undergo grain boundary breakdown is the pores enriched at the grain boundaries. Phase-field simulations indicate that large-sized pores are prone to generate large areas of breakdown phases at their edges, making it easier for breakdown damages to connect with each other and resulting in device failure. Therefore, when preparing FE ceramics, it is advisable to prioritize the elimination of large-sized pores to avoid electric breakdown under low electric fields. Huang et al. combined the grain growth model with the breakdown model to conduct an in-depth study on the changes in Eb during the heat treatment process of FE materials[41]. Phase-field simulations show that during the heat treatment process, the phenomenon of grain aggregation will occur, reducing the surface energy. Grains merge with each other and eliminate small grains that have a high dielectric permittivity and are prone to breakdown, thus improving the overall Eb of the material.
DOMAIN MODULATION STRATEGIES TO ENHANCE POLARIZATION CHANGE
To obtain FE materials with high energy storage performance, in addition to increasing Eb, it is also necessary to reduce Pr to enhance the energy storage density and efficiency. The polarization of FE materials exhibits the characteristic of domains at the mesoscopic scale. The dielectric response of domains always lags behind the external electric field, and the polarization-electric field (P-E) curve shows a hysteresis. Existing research indicates that element doping of FE materials can disrupt the long-range ordered FE domain[85-87]. Although the average polarization intensity decreases as the domain size decreases, it can significantly reduce the Pr of the material, increase ΔP, and improve Wrec. Therefore, studying the dynamic behaviors of domains and polarization under an external electric field at the mesoscopic scale is of great significance for designing FE energy storage materials with high ΔP.
Wang et al. constructed a phase-field model of RFE based on the random field theory[50,88]. This model starts from the thermodynamic theory and takes into account the contributions of the Gaussian-distributed random field to the elastic energy and electrostatic energy. Thus, it realizes the transformation process from FE bulk domains to relaxor nanodomains. The modification of the random field can also make the P-E loop thinner, presenting the characteristics of RFE. Li et al. grasp the characteristics of PNRs in the RFE
Polymorphic nanodomain design strategies
Polymorphic nanodomains refer to the domain structures where multiple phases such as Rhombohedral phase (R-phase), Orthorhombic phase (O-phase), Tetragonal phase (T-phase) or Cubic phase (C-phase) coexist, which are formed through composition design based on RFE. According to the Landau theory, polymorphic domains can reduce the thermodynamic potential barriers between phases. When FE domains undergo phase transitions under an external electric field, only small driving force is needed to overcome the barriers, showing extremely small Pr. Chai et al. fabricate 0.85K0.5Na0.5NbO3-0.15Sr0.7Nd0.2ZrO3 ceramics[89]. The heterogeneous nanostructure of O-phase, T-phase, and C-phases was designed, forming highly dynamic PNRs. Phase-field simulations confirm that this disordered structure weakens energy barriers and polarization anisotropy, enabling the material to exhibit high polarization response and low Pr, thereby enhancing the Wrec and energy efficiency.
Pan et al. adopt the design concept of polymorphic nanodomains and prepare energy storage thin films of the BFO-BTO-STO[27]. There exists a polymorphic nanodomain structure in the film where the paraelectric (PE) phase serves as the matrix and R-phase, T-phase coexist [Figure 7A]. Through high-throughput phase-field simulations, the composition of 0.25BFO-0.3BTO-0.45STO with the highest energy storage performance (112 J/cm3) has been obtained [Figure 7B]. The introduction of the PE-phase STO can break the long-range ordered domain structure of FE and form PNRs. BFO and BTO can form a mixed domain structure of R and T phases, reducing the phase transition barrier.
Figure 7. Domain structures and energy storage properties of FE polymorphic domains by phase-field simulations. (A) BFO-BTO-STO polymorphic domain structure; (B) Energy storage density and efficiency. The figures are quoted with the permission from Pan et al.[27], copyright 2019, AAAS; (C) Simulations of domain structures and P-E loops at 200, 450, 800 and 1,100 K of Sm-BFO-BTO, showing FE, conventional RFE, SPE-RFE and PE features, respectively. The figure is quoted with the permission from Pan et al.[28], copyright 2021, AAAS. FE: Ferroelectric; BFO: BiFeO3; BTO: BaTiO3; STO: SrTiO3; RFE: relaxor ferroelectrics; SPE: superparaelectric; PE: paraelectric.
Subsequently, the team select the Sm-BFO-BTO composition to further study the influence of temperature on the domain structure and energy storage performance[28]. Phase-field simulations show that at room temperature, this composition exhibits ferroelectricity. As the temperature rises and exceeds the freezing temperature (Tf), the material exhibits the characteristics of RFE. When the temperature exceeds the temperature corresponding to the peak temperature of the dielectric permittivity (Tm), a superparaelectric-RFE (SPE-RFE) state where PE phase and RFE phase coexist appears [Figure 7C]. In this state, the domain size decreases from approximately 10 nm in the RFE state to approximately 1.5 nm, and it can maintain a relatively high polarization compared to a PE phase. Eventually, the 10% mol Sm-doped 0.3BFO-0.7BTO composition achieves Wrec of 152 J/cm3 with efficiency exceeding 90%. The temperature factor has thus become an important factor that cannot be ignored in the study of energy storage performance of RFE.
Subsequently, other teams have been working on exploring high-energy-storage RFE with a wide operating temperature range in FE bulk materials. Wang et al. dope NaNbO3 into (Na0.5Bi0.5)0.7Sr0.3TiO3-based materials and obtained ergodic relaxors (ER) over a wide temperature range[90]. Phase-field simulations show that ER state contains high-density PNRs. The PNRs change the polarization characteristics, making the polarization more susceptible to the influence of electric field. Li et al. conduct in-depth research on composition design-induced PNRs in the ceramic bulk systems of BNT and K0.5Na0.5NbO3 (KNN)[91-94]. The results of phase-field simulations show that doping with complex elements can reduce the size of FE domains and obtain PNRs. The total free energy of polymorphic nanodomain structure exhibits the characteristic of thermal fluctuations, enabling RFE to still show a good dielectric response over a wide temperature range.
High-entropy RFE domain design strategies
Guided by the mechanism of nanodomains in reducing the phase transition barrier, research teams have drawn on the design concept of high-entropy alloys to further explore the energy storage performance of high-entropy RFE materials[95,96]. Different from RFE materials, the high-entropy design aims to have elements with different ionic radii and electronegativities occupy lattice sites starting from the lattice size. When the configurational entropy of a material is greater than 1.5 times the gas constant (R), it is regarded as high-entropy RFE. High-entropy RFE has extremely small domain sizes and low Wloss. In addition, the complex crystal structure can increase the transport barrier for charge carriers and improve Eb. The high-entropy design strategy has great application potential in the field of energy storage dielectric materials.
Yang et al. regulate the configurational entropy by introducing elements such as Sr, Ca, La, Na and K into Ba2Bi4Ti5O18-based RFE[97]. The increase in configurational entropy will lead to a decrease in grain size accompanied by the appearance of an amorphous phase. Carriers have high transport barriers at grain boundaries and the amorphous phase, resulting in an increase in Eb. Additionally, the configurational entropy significantly increases local inhomogeneity, bringing about a more disordered polarization distribution, making the P-E loop thinner and improving Wrec [Figure 8A].
Figure 8. Domain structures, P-E loops and energy storage properties of low-entropy, medium-entropy, and high-entropy FE ceramics, respectively, by phase-field simulations. (A) Ba2Bi4Ti5O18-based compositions. The figure is quoted with the permission from Yang et al.[97], copyright 2024, John Wiley and Sons; (B) BFO-based, BTO-based, and PTO-based compositions[98]. BFO: BiFeO3; BTO: BaTiO3; PTO: PbTiO3.
However, the energy storage performance does not always increase with the configurational entropy. In the Bi4Ti3O12-based system, different mechanisms have been reported. Researchers assumed that element doping in high-entropy RFE would lower the TC and introduce point defects. And they selecte multiple sets of potential functions such as those of BTO, PTO, BFO and Bi4Ti3O12 for calculations[99]. Researchers find that after the configurational entropy increases from 0R to 1.6R, although the efficiency is significantly improved, Pm decreases significantly compared to medium-entropy components, resulting in a reduction in Wrec. Peng et al. have fabricated high-entropy ceramics with a composition of (Sr0.2Ba0.2Pb0.2La0.2Na0.2)Nb2O6 (SBPLNN)[100]. This work has focused on the local stress fields generated by element doping in high-entropy RFE and coupled them with the polarization intensity through electrostrictive coefficient. The simulation results show that as the types of A-site elements increase, the compositional inhomogeneity increases, leading to changes in the local stress fields and causing the domain structure to transform from ordered large domains to disordered PNRs to reduce the total free energy of the system.
Since high-entropy FE energy storage materials contain numerous elements, the screening of components demands a large amount of time and resources. To guide the design of high-entropy components, Zhang
Domain modulation strategies via polar-slush state
Polar slush (PS) phase usually refers to the transformation of PNRs into isolated, slush-like polar cluster structures in polycrystalline RFE through element doping and experimental processes[101-103]. In PS phase, the non-polar C-phase is significantly suppressed. Compared with traditional RFE, Pm has been significantly improved. High-density low-angle domain walls or an amorphous-like phase can form a highly insulating network to isolate the slush phase, reducing the size of nanodomains and Pr. Polymorphic domains with a size of about 2-4 nm and continuous polarization transitions, such as O-phase and T-phase, can be found. Tao et al. discovered the PS polarization state in KNN-based ceramics[104]. Phase-field simulations reproduce PNR structure with the coexistence of R-phase, O-phase and T-phase. The three types of PNRs interpenetrate with each other at a scale of about 2 nm, forming the polar-slush polarization state [Figure 9A]. Under an external electric field, the switching barriers among various states are greatly reduced, providing a flexible polarization response.
Figure 9. Polar-slush state of RFE. (A) Phase-field simulation of T-O-R three-phase coexistence in the material and their projection of polarization on the (110) plane with a slush-like state. This figure is quoted with the permission from Tao et al.[104], copyright 2019, American Chemical Society; (B) IPS design roadmap, schematic diagram of structural features, and design purpose. This figure is quoted with the permission from Shu et al.[17], copyright 2024, AAAS. RFE: Relaxor ferroelectrics; IPS: isolated polar-slush.
Shu et al. design BMT-STO-based films and conduct phase-field simulations on RFE state with PNRs, PS state and isolated polar-slush (IPS) state[17]. The results show that in RFE state, R-phase nanodomains are presented in C-phase matrix. PS state exhibits a slush-like polar structure of O-phase and T-phase, and the non-polar C-phase is suppressed. IPS state shows a more significant disorder, and the proportions of O-phase and T-phase are further increased. Research indicates that IPS has obvious advantages in decoupling polarization and hysteresis, significantly improving the energy storage performance [Figure 9B]. In IPS state of the BMT-STO film, an ultra-high Wrec of 202 J/cm3 has been achieved. Yuan et al. use phase-field simulations to study the correlation between the interfacial energy coefficient and the domain structure[105]. The reduction in interfacial energy makes the fractions of R, O and T-phases close to each other and significantly reduces the average domain size, forming a slush-like domain structure. Subsequently, combined with machine learning-assisted component screening, it becomes possible to achieve the coexistence of slush-like multiple phases. Eventually, the target component of 0.9Ba0.82Ca0.18TiO3-0.07BaZrO3-0.03BaSnO3 has been designed and fabricated into thin films, achieving a Wrec of 80 J/cm3 and an energy storage efficiency of 85%.
The structures of PS state domain and nanodomain are different. Polar domain is isolated by the polar matrix, point defects, and cubic phase in PS state. Under the saturated electric field, Pm is much higher than that of nanodomain. At the same time, the long-range ordered FE domains are disrupted, and the hysteresis is minimized. This may become a universal solution to break through the relationship between saturated polarization and hysteresis.
Energy storage enhancement by topological structures
In polycrystalline FE materials, there is a huge dielectric permittivity mismatch between the grain boundaries and the grains. To ensure electrostatic equilibrium and reach the minimum energy, FE polarization near the grain boundaries will be connected head to tail due to the depolarization effect, forming a flux-closure domain. When the grain size is much larger than the FE domain, the volume fraction of grain boundaries is too low and the depolarization effect has no obvious effect on the domain morphology. However, when the grain size is reduced to nanometers, the grain boundaries will have a strong bound effect on the FE domain and FE domain will transform into a stable topological vortex domain[106-109].
Cai et al. select the BTO system to study the influence of grain size on energy storage performance[110]. Phase-field simulations show that when the volume fraction of grain boundaries is high enough or the dielectric permittivity is small enough, it will induce the formation of a vortex state in BTO [Figure 10A]. The vortex domains have a topological protection effect[111-113]. After the electric field is removed, compared with trivial domains, they are more likely to return to vortex state and reduce Pr [Figure 10B]. Qian et al. obtained similar results in BNT-based FE nanocrystals[18]. When the average grain size decreases from 50 to 20 nm, Pm decreases slightly while Pr decreases significantly. Wrec increases by 65% and the energy storage efficiency increases by 58%. Phase-field simulations verify that when the average grain size decreases to be close to domain size (approximately 20 nm), the density of topological vortex domains increases significantly. The generation of vortex domains reduced the anisotropy of polarization and lowered the phase transition barrier, having a significant effect on improving the energy storage performance.
Figure 10. Phase-field simulations of topological domain structures and energy storage performance. (A) Vortex domain and trivial domain under external electric field of BTO core-shell structures; (B) Energy storage performance with different shell fraction and permittivity. This figure is quoted with the permission from Cai et al.[110], copyright 2021, AIP Publishing; (C) Vortex domain, spiral domain, and trivial domain with different misfit strains; (D) Energy storage performance with different strain and electric field. These figures are quoted with permission from Liu et al.[117], copyright 2022, John Wiley and Sons. BTO: BaTiO3.
Besides the process of controlling the grain size to obtain topological vortex domains, the PE-FE multi-layer thin film system is also widely used to obtain high density topological vortex domains[113-116]. Liu et al. use phase-field simulations to construct a three-layer film structure of STO-BFO-STO[117]. Under the effect of high compressive strain (-3.7% to -2.1%), the BFO layer presents a continuous vortex domain configuration. As the compressive strain decreases, the vortex core moves toward the interface and transforms into a spiral-like domain. When a tensile strain of 0.9% is applied, the BFO forms a trivial domain [Figure 10C].
The article also analyzed the influence of film thickness on the topological domain structure. When the thickness of BiFeO3 (BFO) increases, the vortex core has to travel a longer distance before reaching the interface, delaying the phase transition from the vortex domain to the spiral-like domain. Different topological configurations also lead to varying dielectric responses. The vortex domain has a larger phase transition electric field, which is 4-8 MV/m depending on the increase in compressive strain. The spiral-like domain can complete the phase transition below 3 MV/m. The larger phase transition electric field of the vortex domain can be attributed to topological protection. Eventually, STO-BTO-STO three-layer films can achieve a Wrec of 171 J/cm3 and an efficiency of 85% [Figure 10D].
In summary, the flux-closure domains in polycrystalline ceramics, along with the vortex domains and spiral domains in thin films, all possess relatively low free energy due to the topological protection mechanism. When the external electric field is removed, they can rapidly return to topological state. This reduces the hysteresis effectively and enhances energy storage performance.
Domain modulation by strain engineering
Similar to the idea of using strain to regulate the phase transition of topological domain structure in the above to improve energy storage performance, strain engineering is also an effective way to enhance the energy storage performance FE materials. In the preparation of epitaxial films, strain can be applied to the FE films through the lattice mismatch between substrate and film. The mismatch strain will not only change the domain structure, but also significantly affect the dielectric response behavior of domains[112,118].
Wang et al. systematically simulate P-E loops of common FE thin films (such as BTO, STO and BFO) under the regulation of -2% compressive strain to 2% tensile strain[119]. Take the BTO film as an example. Under compressive strain, it presents a typical FE P-E loop with a relatively high Pr. Tensile strain makes the P-E loop thinner. Coercive field and Pr decrease. Films of other systems also have a similar trend. As the strain changes from compressive to tensile, Pm of some films (such as BTO, PZT, KNN, etc.) decreases slightly, but Pr decreases significantly, resulting in an increase in Wrec. Phase-field simulations reveal the mechanism of the effect of strain engineering on the dielectric response from the change of domain structure. Also, taking BTO as an example, under 2% tensile strain, the elastic energy breaks the symmetry of the polarization variants and stabilizes the domain structure in the in-plane O-phase. When the external electric field is removed, it is also easier to return to the initial in-plane state. However, under 2% compressive strain, BTO exhibits an out-plane T-phase, resulting in a higher Pr.
Xu et al. simulate the effect of strain on the domain structure and energy storage performance of BFO-BTO-STO RFE films[120]. Among them, the 0.1BFO-0.45BTO-0.45STO component shows R, T, and C-phases polymorphic domains without misfit strain. As the compressive strain increases, C-phase is gradually replaced by T-phase, transforming into an R/T mixed-phase. As the tensile strain increases, the C-phase is gradually replaced by O-phase [Figure 11A]. The simulation results also show that tensile strain can improve Wrec and energy storage efficiency.
Figure 11. Strain engineering regulates domain structure and energy storage performance. (A) 0.1BFO-0.45BTO-0.45STO thin film domain structure with different strains by substrate. This figure is quoted with the permission from Xu et al.[120], copyright 2022, John Wiley and Sons; (B) P-E loops and polarization distribution of BTO freestanding thin film under different bending strains; (C) Polarization distribution under different bending strains[121]. BFO: BiFeO3; BTO: BaTiO3; STO: SrTiO3.
FE freestanding films have excellent super-elasticity. When bent, a flexoelectric field can be generated, which in turn regulates the domain structure and energy storage performance. Guo et al. construct a phase-field model of super-elastic films and study the influence of bending deformation on the domain structure and dielectric response of FE films such as BTO, BFO, KNN, and PZT[121]. As the bending strain increases from 2% to 4%, the flexoelectric field generated by bending shifts the P-E loop towards the positive voltage direction, facilitating the improvement of Wrec and the energy storage efficiency [Figure 11B]. Meanwhile, the out-plane polarization component PZ decreases [Figure 11C]. Both substrate mismatch strain and bending strain alter the state of the minimum total free energy of FE domain structure through external stress. At the cost of sacrificing Pm, Pr is reduced, and a larger ΔP is obtained under the external electric field. Strain engineering strategy can be integrated with composition design to synergistically regulate the domain structure and improve energy storage performance.
AFE domain modulation strategies
AFE has antiparallel polarization that is different from FE and has a Pr close to zero under zero electric field. Theoretically, AFE materials can achieve a larger ΔP than FE and are expected to achieve a higher Wrec. Thus, beginning with AFE phase-field simulations, this work reviews the mechanism of improving energy storage performance through domain structure regulation. Ma et al. study the heterostructure of AFE PbHfO3 (PHO) and PE BaHfO3 (BHO). The Pb0.5Ba0.5HfO3 component has a RFE-like dielectric response and excellent energy storage performance (20.2 J/cm3)[122]. Phase-field simulations reveal that the appearance of low Pr under zero electric field is due to the in-plane expansion caused by AFE polarization of PHO, which compresses the neighboring BHO unit cells and leads to elongation along the Z-axis.
To further explore the correlation between AFE antiparallel polarization distribution and the dielectric response, Liu et al. develop an AFE phase-field model based on the tilt angle of oxygen octahedrons
Figure 12. PZO-based AFE domain structures and energy storage performance. The local domain structure and polarization displacement with different periodicities (n). (A) n = 4. (B) n = 7. This figure is quoted with permission from Liu et al.[19], copyright 2020, Elsevier; (C) Energy storage density and efficiency of PZO-based incommensurate phase with different strain, layers and defect dipole concentrations. This figure is quoted with permission from Xu et al.[53], copyright 2025, Elsevier. PZO: PbZrO3; AFE: antiferroelectric.
Xu et al. systematically investigate the influence of point defect concentration, substrate misfit strain and thickness on the energy storage performance of PZO-based AFE thin films[53,57], as shown in Figure 12C. The results of phase-field simulations show that local electric field caused by point defects can induce the generation of vortex domains, reduce domain size and decrease Wloss. In-plane tensile strain can increase periodicity of AFE stripe domain, raise the AFE-FE phase transition electric field and enhance Wrec. In addition, an increase in film thickness can enlarge the size of AFE domains, reduce the surface depolarization effect and improve the polarization response.
CONCLUSIONS AND FUTURE OUTLOOK
This article reviews the modification strategies for FE energy storage materials and discusses the guidance of phase-field simulations on the design of materials with high energy storage density and the mechanism of FE domain structures. Due to the difficulty in characterizing the transition dynamics of FE/AFE polarization under the external electric field, phase-field simulations have become an important means to reveal the dynamic mechanism of FE materials. In addition, the design of energy storage materials needs to break the inverted coupling relationship between Eb and ΔP. Phase-field simulations can couple multi-physics-field factors such as temperature, strain field and electric field, and calculate the evolution processes of electric breakdown and polarization from the grain scale to the dipole scale, providing theoretical support for in-depth exploration of improvement strategies for Eb and ΔP.
To better play the guiding role of theoretical calculations in the field of FE energy storage materials, several key issues still need to be focused on in the development of phase-field models. Firstly, the research and development of energy storage materials is a complex physical problem across multi-scales, ranging from atomic-level doping to the fabrication of devices such as MLCC. It is still necessary to further construct phase-field models applicable to the atomic scale and the device scale and explore the design schemes for multi-scale energy storage materials. Moreover, there is an urgent need to develop computational models that combine phase-field simulations with machine learning to obtain quantitative experimental guidance under complex conditions with multi-factors and multi-physical variables. Physics-Informed Machine Learning integrates physical laws into the loss function of neural networks to constrain and guide model training[125]. It reconstructs the multi-physics field and multi-variable coupling problems in phase-field simulations into unsupervised learning tasks, which is expected to significantly improve the solution accuracy and efficiency of phase-field simulations. The physics-informed and data-driven approach, represented by DeepONet model, consists of a branch network and a trunk network[126]. It can learn the mapping between function spaces and has obvious advantages in simulating complex physical mechanisms. It is expected to establish a mapping relationship between the domain structure and multi-physics-field responses, guiding the inverse design of energy storage materials.
DECLARATIONS
Authors’ contributions
Conceived and designed the manuscript: Huang, H.; Wang, J.; Yang, L.; Xu, K.
Drafted and revised the manuscript: Huang, H.; Xu, K.
Availability of data and materials
Not applicable.
Financial support and sponsorship
Huang, H. acknowledged the support of the National Natural Science Foundation of China (92463306, 52372100). Wang, J. acknowledged the support of the National Natural Science Foundation of China (52472119) and Beijing Natural Science Foundation (2242057). Yang, L. acknowledged the support of the National Natural Science Foundation of China (52302277).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Yang, L.; Kong, X.; Li, F.; et al. Perovskite lead-free dielectrics for energy storage applications. Prog. Mater. Sci. 2019, 102, 72-108.
2. Palneedi, H.; Peddigari, M.; Hwang, G.; Jeong, D.; Ryu, J. High-performance dielectric ceramic films for energy storage capacitors: progress and outlook. Adv. Funct. Mater. 2018, 28, 1803665.
3. Sun, Z.; Wang, Z.; Tian, Y.; et al. Progress, outlook, and challenges in lead-free energy-storage ferroelectrics. Adv. Elect. Mater. 2020, 6, 1900698.
4. Luo, S.; Yu, J.; Yu, S.; et al. Significantly enhanced electrostatic energy storage performance of flexible polymer composites by introducing highly insulating-ferroelectric microhybrids as fillers. Adv. Energy. Mater. 2019, 9, 1803204.
5. Hao, Y.; Wang, X.; Bi, K.; et al. Significantly enhanced energy storage performance promoted by ultimate sized ferroelectric BaTiO3 fillers in nanocomposite films. Nano. Energy. 2017, 31, 49-56.
6. Zhang, R.; Li, L.; Long, S.; et al. Linear and ferroelectric effects of BaTiO3 particle size on the energy storage performance of composite films with different polymer matrices. Ceram. Int. 2021, 47, 22155-63.
7. Li, H.; Liu, F.; Fan, B.; Ai, D.; Peng, Z.; Wang, Q. Nanostructured ferroelectric-polymer composites for capacitive energy storage. Small. Methods. 2018, 2, 1700399.
8. Guo, M.; Jiang, J.; Shen, Z.; Lin, Y.; Nan, C.; Shen, Y. High-energy-density ferroelectric polymer nanocomposites for capacitive energy storage: enhanced breakdown strength and improved discharge efficiency. Mater. Today. 2019, 29, 49-67.
9. Sun, Y.; Zhang, L.; Huang, Q.; et al. Ultrahigh energy storage density in glassy ferroelectric thin films under low electric field. Adv. Sci. 2022, 9, e2203926.
10. Peddigari, M.; Wang, B.; Wang, R.; et al. Giant energy density via mechanically tailored relaxor ferroelectric behavior of PZT thick film. Adv. Mater. 2023, 35, 2302554.
11. Zhu, M.; Huang, X.; Yang, K.; et al. Energy storage in ferroelectric polymer nanocomposites filled with core-shell structured polymer@BaTiO3 nanoparticles: understanding the role of polymer shells in the interfacial regions. ACS. Appl. Mater. Interfaces. 2014, 6, 19644-54.
12. Wu, L.; Wang, X.; Li, L.; Randall, C. Enhanced energy density in core–shell ferroelectric ceramics: modeling and practical conclusions. J. Am. Ceram. Soc. 2016, 99, 930-7.
13. Yang, F.; Zhao, H.; Zhang, C.; et al. Improved energy storage property of ferroelectric polymer-based sandwiched composites interlayered with graphene oxide @ SiO2 core–shell nanoplatelets. J. Mater. Sci. 2022, 57, 11824-38.
14. Feng, M.; Feng, Y.; Zhang, T.; et al. Recent advances in multilayer-structure dielectrics for energy storage application. Adv. Sci. 2021, 8, 2102221.
15. Wang, G.; Lu, Z.; Li, Y.; et al. Electroceramics for high-energy density capacitors: current status and future perspectives. Chem. Rev. 2021, 121, 6124-72.
16. Sturge, K. M.; Hoppis, N.; Bussio, A. M.; et al. Dynamics of high-speed electrical tree growth in electron-irradiated polymethyl methacrylate. Science 2024, 385, 300-4.
17. Shu, L.; Shi, X.; Zhang, X.; et al. Partitioning polar-slush strategy in relaxors leads to large energy-storage capability. Science 2024, 385, 204-9.
18. Qian, J.; Yu, Z.; Ge, G.; et al. Topological vortex domain engineering for high dielectric energy storage performance. Adv. Energy. Mater. 2024, 14, 2303409.
19. Liu, H.; Zhou, Z.; Qiu, Y.; et al. An intriguing intermediate state as a bridge between antiferroelectric and ferroelectric perovskites. Mater. Horiz. 2020, 7, 1912-8.
20. Wu, L.; Cai, Z.; Zhu, C.; Feng, P.; Li, L.; Wang, X. Significantly enhanced dielectric breakdown strength of ferroelectric energy-storage ceramics via grain size uniformity control: Phase-field simulation and experimental realization. Appl. Phys. Lett. 2020, 117, 212902.
21. Bi, K.; Bi, M.; Hao, Y.; et al. Ultrafine core-shell BaTiO3@SiO2 structures for nanocomposite capacitors with high energy density. Nano. Energy. 2018, 51, 513-23.
22. Chen, B.; Zhu, W.; Wang, T.; et al. Ultrahigh energy storage capacitors based on freestanding single-crystalline antiferroelectric membrane/PVDF composites. Adv. Funct. Mater. 2023, 33, 2302683.
23. Sun, J.; Yang, C.; Song, J.; Zhou, Y.; Yao, Q.; Sun, X. The microstructure, ferroelectric and dielectric behaviors of
24. Yang, B. B.; Guo, M. Y.; Song, D. P.; et al. Bi3.25La0.75Ti3O12 thin film capacitors for energy storage applications. Appl. Phys. Lett. 2017, 111, 183903.
25. Tong, S.; Ma, B.; Narayanan, M.; et al. Lead lanthanum zirconate titanate ceramic thin films for energy storage. ACS. Appl. Mater. Interfaces. 2013, 5, 1474-80.
26. Pan, H.; Zeng, Y.; Shen, Y.; et al. BiFeO3–SrTiO3 thin film as a new lead-free relaxor-ferroelectric capacitor with ultrahigh energy storage performance. J. Mater. Chem. A. 2017, 5, 5920-6.
27. Pan, H.; Li, F.; Liu, Y.; et al. Ultrahigh-energy density lead-free dielectric films via polymorphic nanodomain design. Science 2019, 365, 578-82.
28. Pan, H.; Lan, S.; Xu, S.; et al. Ultrahigh energy storage in superparaelectric relaxor ferroelectrics. Science 2021, 374, 100-4.
29. Lee, H. J.; Won, S. S.; Cho, K. H.; et al. Flexible high energy density capacitors using La-doped PbZrO3 anti-ferroelectric thin films. Appl. Phys. Lett. 2018, 112, 092901.
30. Hao, X.; Wang, Y.; Yang, J.; An, S.; Xu, J. High energy-storage performance in Pb0.91La0.09(Ti0.65Zr0.35)O3 relaxor ferroelectric thin films. J. Appl. Phys. 2012, 112, 114111.
31. Lin, Z.; Chen, Y.; Liu, Z.; Wang, G.; Rémiens, D.; Dong, X. Large energy storage density, low energy loss and highly stable
32. Ali, F.; Liu, X.; Zhou, D.; et al. Silicon-doped hafnium oxide anti-ferroelectric thin films for energy storage. J. Appl. Phys. 2017, 122, 144105.
33. Acharya, M.; Banyas, E.; Ramesh, M.; et al. Exploring the Pb1-xSrxHfO3 system and potential for high capacitive energy storage density and efficiency. Adv. Mater. 2022, 34, 2105967.
34. Yang, B.; Liu, Y.; Jiang, R. J.; et al. Enhanced energy storage in antiferroelectrics via antipolar frustration. Nature 2025, 637, 1104-10.
35. Cheng, H.; Ouyang, J.; Zhang, Y. X.; et al. Demonstration of ultra-high recyclable energy densities in domain-engineered ferroelectric films. Nat. Commun. 2017, 8, 1999.
36. Wang, J.; Shi, S.; Chen, L.; Li, Y.; Zhang, T. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta. Mater. 2004, 52, 749-64.
37. Gao, R.; Shi, X.; Wang, J.; Zhang, G.; Huang, H. Designed giant room-temperature electrocaloric effects in metal-free organic perovskite [MDABCO](NH4)I3 by phase–field simulations. Adv. Funct. Mater. 2021, 31, 2104393.
38. Wang, J.; Ma, X.; Li, Q.; Britson, J.; Chen, L. Phase transitions and domain structures of ferroelectric nanoparticles: Phase field model incorporating strong elastic and dielectric inhomogeneity. Acta. Mater. 2013, 61, 7591-603.
39. Choudhury, S.; Li, Y.; Krilliii, C.; Chen, L. Phase-field simulation of polarization switching and domain evolution in ferroelectric polycrystals. Acta. Mater. 2005, 53, 5313-21.
40. Xu, B. X.; Schrade, D.; Gross, D.; Mueller, R. Fracture simulation of ferroelectrics based on the phase field continuum and a damage variable. Int. J. Fract. 2010, 166, 163-72.
41. Huang, S.; Duan, Z.; Chen, J.; et al. Phase-field modeling for energy storage optimization in ferroelectric ceramics capacitors during heat treatment process. Ceram. Int. 2024, 50, 52020-6.
42. Shen, Z. H.; Wang, J. J.; Lin, Y.; Nan, C. W.; Chen, L. Q.; Shen, Y. High-throughput phase-field design of high-energy-density polymer nanocomposites. Adv. Mater. 2018, 30, 1704380.
43. Shen, Z.; Bao, Z.; Cheng, X.; et al. Designing polymer nanocomposites with high energy density using machine learning. npj. Comput. Mater. 2021, 7, 578.
44. Shen, Z.; Wang, J.; Jiang, J.; et al. Phase-field model of electrothermal breakdown in flexible high-temperature nanocomposites under extreme conditions. Adv. Energy. Mater. 2018, 8, 1800509.
45. Li, F.; Zhang, S.; Yang, T.; et al. The origin of ultrahigh piezoelectricity in relaxor-ferroelectric solid solution crystals. Nat. Commun. 2016, 7, 13807.
46. Li, F.; Zhang, S.; Xu, Z.; Chen, L. The contributions of polar nanoregions to the dielectric and piezoelectric responses in domain-engineered relaxor-PbTiO3 crystals. Adv. Funct. Mater. 2017, 27, 1700310.
47. Shi, X.; Wang, J.; Xu, J.; Cheng, X.; Huang, H. Quantitative investigation of polar nanoregion size effects in relaxor ferroelectrics. Acta. Mater. 2022, 237, 118147.
48. Glinchuk, M. D.; Farhi, R. A random field theory based model for ferroelectric relaxors. J. Phys. Condens. Matter. 1996, 8, 6985.
49. Hong, Z.; Ke, X.; Wang, D.; Yang, S.; Ren, X.; Wang, Y. Role of point defects in the formation of relaxor ferroelectrics. Acta. Mater. 2022, 225, 117558.
50. Wang, S.; Yi, M.; Xu, B. A phase-field model of relaxor ferroelectrics based on random field theory. Int. J. Solids. Struct. 2016, 83, 142-53.
51. Song, Y.; Shi, X.; Wang, J.; Huang, H. Predicting dielectric properties of ferroelectric materials with point defects by a phase-field model. ACS. Appl. Electron. Mater. 2024, 6, 3726-33.
52. Song, Y.; Xu, K.; Wang, J.; Huang, H. Thickness-dependent dielectric properties in doped relaxor films by the phase-field model. ACS. Appl. Electron. Mater. 2024, 6, 6477-83.
53. Xu, K.; Tang, S.; Guo, C.; Song, Y.; Huang, H. Antiferroelectric domain modulation enhancing energy storage performance by phase-field simulations. J. Materiomics. 2025, 11, 100901.
54. Lin, B.; Ong, K. P.; Yang, T.; et al. Ultrahigh electromechanical response from competing ferroic orders. Nature 2024, 633, 798-803.
55. Xue, F.; Liang, L.; Gu, Y.; Takeuchi, I.; Kalinin, S. V.; Chen, L. Composition- and pressure-induced ferroelectric to antiferroelectric phase transitions in Sm-doped BiFeO3 system. Appl. Phys. Lett. 2015, 106, 012903.
56. Xu, K.; Shi, X.; Shao, C.; Dong, S.; Huang, H. Design of polar boundaries enhancing negative electrocaloric performance by antiferroelectric phase-field simulations. npj. Comput. Mater. 2024, 10, 1334.
57. Xu, K.; Shi, X.; Dong, S.; Wang, J.; Huang, H. Antiferroelectric phase diagram enhancing energy-storage performance by phase-field simulations. ACS. Appl. Mater. Interfaces. 2022, 14, 25770-80.
58. Li, Q.; Liu, F.; Yang, T.; et al. Sandwich-structured polymer nanocomposites with high energy density and great charge-discharge efficiency at elevated temperatures. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 9995-10000.
59. Shen, Z.; Wang, J.; Zhang, X.; et al. Space charge effects on the dielectric response of polymer nanocomposites. Appl. Phys. Lett. 2017, 111, 092901.
60. Zou, K.; Shao, C.; Bai, P.; et al. Giant room-temperature electrocaloric effect of polymer-ceramic composites with orientated BaSrTiO3 nanofibers. Nano. Lett. 2022, 22, 6560-6.
61. Bao, Z.; Hou, C.; Shen, Z.; et al. Negatively charged nanosheets significantly enhance the energy-storage capability of polymer-based nanocomposites. Adv. Mater. 2020, 32, 1907227.
62. Li, Z.; Shen, Z.; Yang, X.; et al. Ultrahigh charge-discharge efficiency and enhanced energy density of the sandwiched polymer nanocomposites with poly(methyl methacrylate) layer. Compos. Sci. Technol. 2021, 202, 108591.
63. Qian, J.; Peng, R.; Shen, Z.; et al. Interfacial coupling boosts giant electrocaloric effects in relaxor polymer nanocomposites: in situ characterization and phase-field simulation. Adv. Mater. 2019, 31, 1801949.
64. Cai, Z.; Wang, X.; Li, L.; Hong, W. Electrical treeing: a phase-field model. Extreme. Mech. Lett. 2019, 28, 87-95.
65. Cai, Z.; Wang, X.; Luo, B.; Hong, W.; Wu, L.; Li, L. Nanocomposites with enhanced dielectric permittivity and breakdown strength by microstructure design of nanofillers. Compos. Sci. Technol. 2017, 151, 109-14.
66. Shen, Z.; Shen, Y.; Cheng, X.; Liu, H.; Chen, L.; Nan, C. High-throughput data-driven interface design of high-energy-density polymer nanocomposites. J. Materiomics. 2020, 6, 573-81.
67. Wang, Z.; Feng, Z.; Tang, H.; et al. Effects of nanofibers orientation and aspect ratio on dielectric properties of nanocomposites: a phase-field simulation. ACS. Appl. Mater. Interfaces. 2022, 14, 42513-21.
68. Dong, X.; Hu, T.; Wu, X.; Yin, J.; Fu, Z.; Wu, J. A novel lead-free relaxor with endotaxial nanostructures for capacitive energy storage. SusMat 2024, 4, 116-25.
69. Wang, T.; Shi, X.; Peng, R.; et al. Giant energy storage of flexible composites by embedding superparaelectric single-crystal membranes. Nano. Energy. 2023, 113, 108511.
70. Cai, Z.; Zhu, C.; Wang, H.; et al. Giant dielectric breakdown strength together with ultrahigh energy density in ferroelectric bulk ceramics via layer-by-layer engineering. J. Mater. Chem. A. 2019, 7, 17283-91.
71. Guo, Y.; Zhao, W.; Li, D.; et al. Ultra-high capacitive energy storage density at 150 °C achieved in polyetherimide composite films by filler and structure design. Adv. Mater. 2025, 37, e2415652.
72. Jiang, J.; Shen, Z.; Cai, X.; et al. Polymer nanocomposites with interpenetrating gradient structure exhibiting ultrahigh discharge efficiency and energy density. Adv. Energy. Mater. 2019, 9, 1803411.
73. Zhao, P.; Cai, Z.; Chen, L.; et al. Ultra-high energy storage performance in lead-free multilayer ceramic capacitors via a multiscale optimization strategy. Energy. Environ. Sci. 2020, 13, 4882-90.
74. Khondabi, M.; Ahmadvand, H.; Javanbakht, M. Revisiting the dielectric breakdown in a polycrystalline ferroelectric: a phase-field simulation study. Adv. Theory. Simul. 2023, 6, 2200314.
75. Shen, Y.; Wu, L.; Zhao, J.; et al. Constructing novel binary Bi0.5Na0.5TiO3-based composite ceramics for excellent energy storage performances via defect engineering. Chem. Eng. J. 2022, 439, 135762.
76. Li, H.; Pan, Z.; Chen, X.; et al. Stable relaxor ferroelectric phase of NaNbO3-based ceramic with superb energy storage performances. Mater. Today. Phys. 2023, 38, 101208.
77. Huang, J.; Deng, L.; Zhang, Y.; et al. Realizing ultrahigh energy storage density in (Bi0.5Na0.5)0.94Ba0.06TiO3-based ceramics via manipulating the domain configuration and grain boundary density. ACS. Appl. Mater. Interfaces. 2024, 16, 57334-45.
78. Ye, H.; Yang, F.; Pan, Z.; et al. Significantly improvement of comprehensive energy storage performances with lead-free relaxor ferroelectric ceramics for high-temperature capacitors applications. Acta. Mater. 2021, 203, 116484.
79. Wang, X.; Huan, Y.; Zhao, P.; et al. Optimizing the grain size and grain boundary morphology of (K,Na)NbO3-based ceramics: paving the way for ultrahigh energy storage capacitors. J. Materiomics. 2021, 7, 780-9.
80. Yang, B.; Zhang, Y.; Pan, H.; et al. High-entropy enhanced capacitive energy storage. Nat. Mater. 2022, 21, 1074-80.
81. Cai, Z.; Wang, X.; Hong, W.; Luo, B.; Zhao, Q.; Li, L. Grain-size–dependent dielectric properties in nanograin ferroelectrics. J. Am. Ceram. Soc. 2018, 101, 5487-96.
82. Wei, K.; Duan, J.; Li, G.; Yu, H.; Qi, H.; Li, H. Enhancing comprehensive energy storage properties in Pb-free relaxor AFE/FE system via heterogeneous structure tuning and defect engineering. Acta. Mater. 2024, 278, 120278.
83. Li, Y.; Chang, Z.; Zhang, M.; et al. Realizing outstanding energy storage performance in KBT-based lead-free ceramics via suppressing space charge accumulation. Small 2024, 20, e2401229.
84. Cai, Z.; Feng, P.; Zhu, C.; Wang, X. Dielectric breakdown behavior of ferroelectric ceramics: the role of pores. J. Eur. Ceram. Soc. 2021, 41, 2533-8.
85. Yang, L.; Kong, X.; Li, Q.; Lin, Y. H.; Zhang, S.; Nan, C. W. Excellent energy storage properties achieved in sodium niobate-based relaxor ceramics through doping tantalum. ACS. Appl. Mater. Interfaces. 2022, 14, 32218-26.
86. Yang, L.; Kong, X.; Lin, Y.; Zhang, S.; Nan, C. Improved energy storage performance of NaNbO3-based antiferroelectrics by tuning polarizability and defect engineering. J. Am. Ceram. Soc. 2024, 107, 1848-58.
87. Yang, L.; Kong, X.; Cheng, Z.; Zhang, S. Ultra-high energy storage performance with mitigated polarization saturation in lead-free relaxors. J. Mater. Chem. A. 2019, 7, 8573-80.
88. Westphal, V.; Kleemann, W.; Glinchuk, M. D. Diffuse phase transitions and random-field-induced domain states of the “relaxor” ferroelectric PbMg1/3Nb2/3O3. Phys. Rev. Lett. 1992, 68, 847.
89. Chai, Q.; Liu, Z.; Deng, Z.; et al. Excellent energy storage properties in lead-free ferroelectric ceramics via heterogeneous structure design. Nat. Commun. 2025, 16, 1633.
90. Wang, W.; Zhang, L.; Shi, W.; et al. Enhanced energy storage properties in lead-free (Na0.5Bi0.5)0.7Sr0.3TiO3-based relaxor ferroelectric ceramics through a cooperative optimization strategy. ACS. Appl. Mater. Interfaces. 2023, 15, 6990-7001.
91. Li, D.; Zhou, D.; Wang, D.; et al. Lead-free relaxor ferroelectric ceramics with ultrahigh energy storage densities via polymorphic polar nanoregions design. Small 2023, 19, 2206958.
92. Li, D.; Xu, D.; Zhao, W.; et al. A high-temperature performing and near-zero energy loss lead-free ceramic capacitor. Energy. Environ. Sci. 2023, 16, 4511-21.
93. Li, D.; Zhou, D.; Wang, D.; Zhao, W.; Guo, Y.; Shi, Z. Improved energy storage properties achieved in (K, Na)NbO3-based relaxor ferroelectric ceramics via a combinatorial optimization strategy. Adv. Funct. Mater. 2022, 32, 2111776.
94. Zhao, W.; Xu, D.; Li, D.; et al. Broad-high operating temperature range and enhanced energy storage performances in lead-free ferroelectrics. Nat. Commun. 2023, 14, 5725.
95. Zhang, M.; Lan, S.; Yang, B. B.; et al. Ultrahigh energy storage in high-entropy ceramic capacitors with polymorphic relaxor phase. Science 2024, 384, 185-9.
96. Huang, W.; Chen, J.; Zhang, R.; et al. Effect of deformation modes on continuous dynamic recrystallization of extruded AZ31 Mg alloy. J. Alloys. Compd. 2022, 897, 163086.
97. Yang, B.; Liu, Y.; Gong, C.; et al. Design of high-entropy relaxor ferroelectrics for comprehensive energy storage enhancement. Adv. Funct. Mater. 2024, 34, 2409344.
98. Li, W.; Shen, Z. H.; Liu, R. L.; et al. Generative learning facilitated discovery of high-entropy ceramic dielectrics for capacitive energy storage. Nat. Commun. 2024, 15, 4940.
99. Yang, B.; Zhang, Q.; Huang, H.; et al. Engineering relaxors by entropy for high energy storage performance. Nat. Energy. 2023, 8, 956-64.
100. Peng, H.; Wu, T.; Liu, Z.; et al. High-entropy relaxor ferroelectric ceramics for ultrahigh energy storage. Nat. Commun. 2024, 15, 5232.
101. Sun, Z.; Zhang, J.; Luo, H.; et al. Superior capacitive energy-storage performance in Pb-free relaxors with a simple chemical composition. J. Am. Chem. Soc. 2023, 145, 6194-202.
102. Luo, J.; Zhu, H.; Zheng, T.; Qian, H.; Liu, Y.; Lyu, Y. A slush-like polar structure for high energy storage performance in a Sr0.7Bi0.2TiO3 lead-free relaxor ferroelectric thin film. J. Mater. Chem. A. 2022, 10, 7357-65.
103. Wang, H.; Wu, S.; Fu, B.; et al. Hierarchically polar structures induced superb energy storage properties for relaxor Bi0.5Na0.5TiO3-based ceramics. Chem. Eng. J. 2023, 471, 144446.
104. Tao, H.; Wu, H.; Liu, Y.; et al. Ultrahigh performance in lead-free piezoceramics utilizing a relaxor slush polar state with multiphase coexistence. J. Am. Chem. Soc. 2019, 141, 13987-94.
105. Yuan, R.; Kumar, A.; Zhuang, S.; et al. Machine learning-enabled superior energy storage in ferroelectric films with a slush-like polar state. Nano. Lett. 2023, 23, 4807-14.
106. Liu, Z.; Yang, B.; Cao, W.; Fohtung, E.; Lookman, T. Enhanced energy storage with polar vortices in ferroelectric nanocomposites. Phys. Rev. Appl. 2017, 8, 034014.
107. Hou, X.; Li, X.; Zhang, J.; Bag, S. P.; Li, H.; Wang, J. Effect of grain size on the electrocaloric properties of polycrystalline ferroelectrics. Phys. Rev. Appl. 2021, 15, 054019.
108. Wang, Z.; Bin, C.; Zheng, S.; Wang, J. Effect of grain size and grain boundary on the energy storage performance of polycrystalline ferroelectrics. Appl. Phys. Lett. 2024, 125, 152903.
109. Zhu, C.; Cai, Z.; Xiao, M.; et al. Boosting effective capacitance of nanograined BaTiO3-based ceramics via a precise core-shell-structure optimization strategy. J. Alloys. Compd. 2024, 984, 174037.
110. Cai, Z.; Zhu, C.; Wu, L.; Luo, B.; Feng, P.; Wang, X. Vortex domain configuration for energy-storage ferroelectric ceramics design: a phase-field simulation. Appl. Phys. Lett. 2021, 119, 032901.
111. Wang, J.; Liang, D.; Ma, J.; et al. Polar Solomon rings in ferroelectric nanocrystals. Nat. Commun. 2023, 14, 3941.
112. Liu, D.; Wang, J.; Jafri, H. M.; et al. Phase-field simulations of vortex chirality manipulation in ferroelectric thin films. npj. Quantum. Mater. 2022, 7, 444.
113. Das, S.; Hong, Z.; Stoica, V. A.; et al. Local negative permittivity and topological phase transition in polar skyrmions. Nat. Mater. 2021, 20, 194-201.
114. Das, S.; Tang, Y. L.; Hong, Z.; et al. Observation of room-temperature polar skyrmions. Nature 2019, 568, 368-72.
115. Zhou, L.; Huang, Y.; Das, S.; et al. Local manipulation and topological phase transitions of polar skyrmions. Matter 2022, 5, 1031-41.
116. Du, G.; Zhou, L.; Huang, Y.; Wu, Y.; Tian, H.; Hong, Z. Design of polar skyrmion-based nanoelectronic prototype devices with phase-field simulations. Adv. Funct. Mater. 2024, 34, 2405594.
117. Liu, Y.; Liu, J.; Pan, H.; et al. Phase-field simulations of tunable polar topologies in lead-free ferroelectric/paraelectric multilayers with ultrahigh energy-storage performance. Adv. Mater. 2022, 34, 2108772.
118. Zhao, Y.; Ouyang, J.; Wang, K.; et al. Achieving an ultra-high capacitive energy density in ferroelectric films consisting of superfine columnar nanograins. Energy. Storage. Mater. 2021, 39, 81-8.
119. Wang, J.; Su, Y.; Wang, B.; Ouyang, J.; Ren, Y.; Chen, L. Strain engineering of dischargeable energy density of ferroelectric thin-film capacitors. Nano. Energy. 2020, 72, 104665.
120. Xu, S.; Shi, X.; Pan, H.; et al. Strain engineering of energy storage performance in relaxor ferroelectric thin film capacitors. Adv. Theory. Simul. 2022, 5, 2100324.
121. Guo, C.; Yang, H.; Dong, S.; et al. Advancing energy-storage performance in freestanding ferroelectric thin films: insights from phase-field simulations. Adv. Elect. Mater. 2024, 10, 2400001.
122. Ma, C. H.; Liao, Y. K.; Zheng, Y.; et al. Synthesis of a new ferroelectric relaxor based on a combination of antiferroelectric and paraelectric systems. ACS. Appl. Mater. Interfaces. 2022, 14, 22278-86.
123. Zhu, J.; Liu, Z.; Zhong, B.; Wang, Y.; Xu, B. Domain size and charge defects affecting the polarization switching of antiferroelectric domains. Chinese. Phys. B. 2023, 32, 047701.
124. Wang, J.; Fan, X.; Liu, Z.; et al. Superior energy storage performance realized in antiferroelectric 0.10 wt% MnO2–AgNbO3 ceramics via Bi-doping induced phase engineering. J. Mater. Chem. A. 2023, 11, 22512-21.
125. Karniadakis, G. E.; Kevrekidis, I. G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422-40.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data








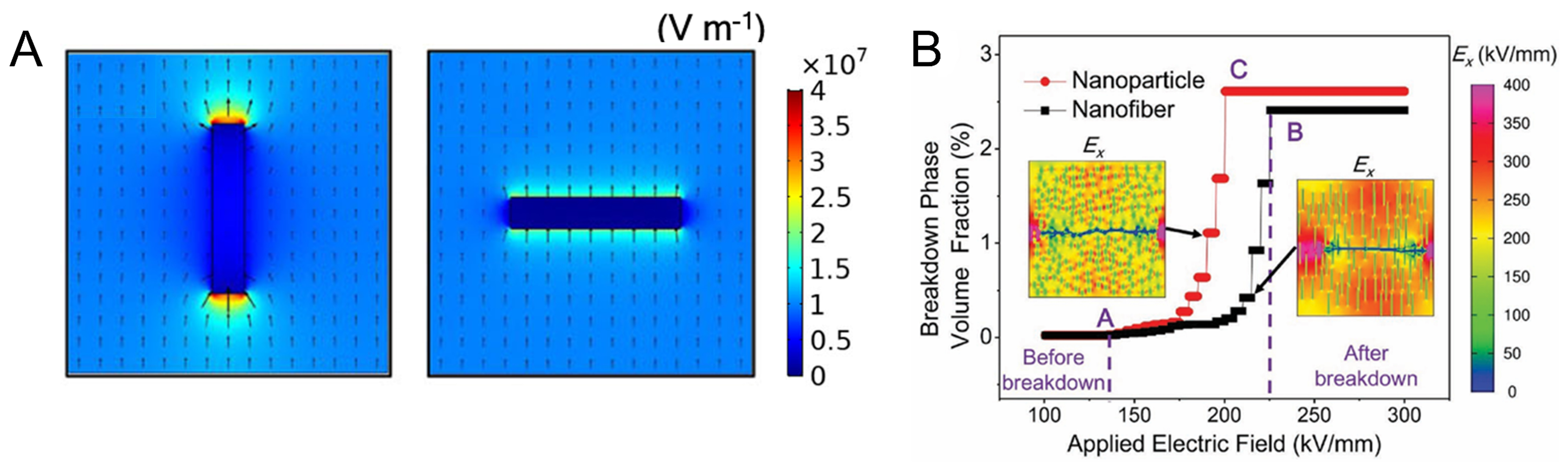





















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].