Equivalent doping of Te leads to optimized electrical and thermal transport properties in thermoelectric Cu₂MnSnSe₄ alloys

INTRODUCTION

The energy crisis and environmental concerns have consistently driven the pursuit of sustainable energy. An increasing number of advanced energy materials, such as dielectric high entropy energy materials, solar cell energy materials and lithium-ion battery energy materials, have attracted widespread attention^[1-3]. Additionally, thermoelectric materials and devices can convert waste heat into electric energy without causing environmental pollution, thus providing a new solution for alleviating the energy crisis and promoting green renewable energy^[4,5]. However, the search for high-performance thermoelectric materials is a major obstacle to the widespread application of thermoelectric technology on a large scale^[6]. The properties of thermoelectric materials are determined by the dimensionless figure of merit (zT = S²σT/κ_tot), where S²σ stands for the power factor (PF), T stands for the absolute temperature, and κ_tot indicates the total thermal conductivity (κ_tot = κ_L + κ_e, where κ_e and κ_L refer to electronic and lattice thermal conductivity, respectively). It is evident that a thermoelectric material with excellent performance should keep high PF and low κ_tot, but these parameters are interrelated^[7]. Achieving optimal electrical and thermal transport performance simultaneously is challenging, making it difficult to attain a satisfactory zT^[7,8]. Over the past two decades of research, many strategies have been successfully implemented in existing systems (Bi₂Te₃, PbTe, and GeTe)^[9-12] to optimize thermoelectric parameters and increase zT, such as modulation doping^[13,14], energy band engineering^[15,16] and energy filtering effects^[17], to optimize electrical transport performance; entropy engineering^[18,19], defect engineering^[20,21] and nanoengineering^[22,23] are used to optimize thermal transport performance.

The development of high-performance thermoelectric materials should focus on not only optimizing existing systems, but also developing potential thermoelectric materials. Elements-rich quaternary chalcogenides have attracted widespread attention due to their intrinsic low thermal conductivity^[24]. The crystal structure of quaternary chalcogenide is derived from a ZnSe supercell arranged in a double-periodic manner along the Z axis, with the Zn site being substituted by three different cations^[25]. With the mismatch of atomic size between the substituting elements, Se atoms deviates from the original ideal tetrahedral position, resulting in lattice distortion and modification of the crystal structure from high-symmetry cubic structure to low-symmetry non-cubic structure, which is conducive to enhancing phonon scattering and inhibiting κ_L^[26,27]. Quaternary chalcogenides have a pseudocubic crystal structure and use the structural distortion parameter (η = c/2a, where c and a are lattice parameters along the z-axis and x-axis, respectively) to reflect their symmetry of crystal structure. Quaternary chalcogenides with η close to 1 usually have better electrical properties^[26]. The reduction of the crystal structure's symmetry can disturb the original periodicity of the lattice and deteriorate the electrical performance. Therefore, preserving the symmetry of the crystal structure is crucial for the thermoelectric properties. Cu₂MnSnSe₄ has been discovered in recent years but it has a relatively wide bandgap (0.7 eV) and poor electrical performance^[27], which limits zT. Many previous studies have successfully optimized Cu₂MnSnSe₄ carrier concentrations (n_H) through the non-stoichiometric Cu^[27] and In doping^[28]. Additionally, we have made progress in regulating the low thermal conductivity of Cu₂MnSnSe₄ by manipulating configurational entropy^[19] and lattice strain^[29]. However, there remains considerable potential for further enhancement of thermoelectric performance. In addition, it can be found that Te doping is particularly interesting and effective in many alloys for improving their thermoelectric performance. Some classical XTe (X:Bi, Sn, Pb)^[9-12] alloys have also achieved cutting-edge zT due to their unique band properties and crystal structures. Therefore, the equivalent doping of Te can further optimize the thermoelectric performance of Cu₂MnSnSe₄.

In this work, the electrical and thermal transport properties of Cu₂MnSnSe₄ were simultaneously optimized through self-doping with Cu and doping with Te. A series of samples, including Cu₂MnSnSe₄ (S-1) and Cu_2.1Mn_0.9SnSe_4-xTe_x (x = 0, 0.01, 0.05, 0.10; S-2 to S-5), were prepared. An analysis was conducted on their crystal structures and electrical and thermal transport properties. At 673 K, the Cu_2.1Mn_0.9SnSe_3.9Te_0.1 sample obtained the lowest κ_L of 0.6 W m^-1K^-1. Within the measured temperature range, all doped samples exhibited enhanced zT. Ultimately, the Cu_2.1Mn_0.9SnSe_3.9Te_0.1 sample obtained a maximum zT of ~ 0.5 at 673 K, representing approximately twice that of the Cu₂MnSnSe₄ sample.

EXPERIMENTAL SECTION

The elements Cu, Mn, Sn, Se, and Te (Aladdin, powder, purity > 99.9%) were weighed out in atomic proportions of S-1 to S-5 and then placed in a stainless steel tank (this was done in a glove box under an argon atmosphere). The tank was placed on a high-energy ball-milling machine and run for 10 h at 500 rpm. After the operation, the powder was placed into a graphite tool for hot pressing under vacuum at 873 K and a pressure of 60 MPa for 1 h. After the hot pressing, the sample, which had cooled to room temperature, was taken out and re-ground into powder form. The hot-pressing operation was repeated under the same conditions. Finally, a high-density disc-shaped sample was obtained.

The chemical compositions and phase structures of the sample powder were analyzed by Rigaku Smartlab X-ray diffractometer with Cu Kα radiation. The samples were refined using the Fullprof software for Rietveld refinements. The microstructure of the samples was analyzed by scanning electron microscopy (SEM; JSM-7610F). The valence state of the sample elements was analyzed using X-ray photoelectron spectroscopy (XPS) by Thermo Scientific K-Alpha instrument. The electrical conductivity (σ) and Seebeck coefficient (S) of the samples were tested by the LINSEIS LSR-3 instrument, within a temperature range from 323 to 673 K. The thermal diffusion coefficient (D) was tested by a laser flash method (TA, DLF-1200). The experimental density (ρ_e) of the sample was determined using the principle of Archimedes. The Dulong-Petit model was employed to estimate the heat capacity (C_p). The κ_tot was calculated by κ_tot = DC_pρ_e. The Hall coefficient of the sample was measured at room temperature by a homemade test apparatus (magnetic field range of ± 1 T). The Hall n_H and carrier mobility (μ_H) at room temperature were calculated using n_H = 1/eR_H and μ_H = σR_H, respectively, where e stands for the number of electron charges and σ represents conductivity. The transverse sound velocity (ν_t) and longitudinal sound velocity (ν_l) of the sample were measured by an ultrasonic pulse receiver (5073PR, OLYMPUS).

RESULTS AND DISCUSSION

To confirm the phase purity of the samples after ball-milling and hot-pressing, X-ray diffraction (XRD) measurements were conducted for all samples. The XRD patterns of each sample are shown in Figure 1A. The sample's primary peaks correspond well to the tetragonal stannite structure (ICSD#155904) and then conducted local amplifications of the XRD patterns for all samples [Supplementary Figure 1]. The XRD peaks did indeed shift by a certain angle, as expected. To further ascertain the crystalline structure of the sample, taking S-5 as an example, using Fullprof software for Rietveld refinements [Figure 1B]. The Rietveld refinements calculation details for the remaining samples are presented in Supplementary Figure 2. The lattice parameters of all samples along the z and x axes (c and a) showed a slight change [Figure 1C], which is caused by the locality of point defects resulting from Te replacing Se and the low Te doping content. This phenomenon has also been observed in other quaternary chalcogenides^[21,30,31]. The structure distortion parameters of all samples were calculated based on the lattice parameters calculated by Rietveld refinements, as shown in Figure 1D. Under the influence of the crystal field effect in quaternary chalcogenides, the triply degenerate valence band Γ_15V of the cubic zinc blende structure splits into a non-degenerate band Γ_4V and a doubly degenerate band Γ_5V, resulting in a splitting energy Δ_CF defined as Δ_CF = E(Γ_5V) - E(Γ_4V). When η approaches 1, the sample displays high symmetry, and the Δ_CF will be closer to 0, which is more favorable for maintaining better electrical properties^[26]. All samples show η values above 0.98, indicating their high symmetry.

Figure 1. (A) Samples powder XRD pattern at room temperature (B) Rietveld refinement of S-5 with Fullprof software (C) The lattice parameters (a & b, c) of samples, (D) The relationship between structure distortion parameters η and band structure of samples^[19].

The microstructure of the fracture surface of the sample was studied using SEM, and the results are depicted in Figure 2A-E. It was found that there are no obvious holes or cracks in all the samples within the entire scanning range and the grain size of the samples is less than five micrometers. These results show that the synthesized sample has a high density (≥ 96%), which corresponds to the high density measured in the experiment [Table 1]. To investigate the uniformity of element distribution in the sample, energy dispersive spectroscopy (EDS) analysis was conducted with S-5 as an example. As shown in Figure 2F-K, all elements Cu, Mn, Sn, Se and Te were uniformly distributed with no significant aggregation or dispersion observed. Additionally, the mass fraction of each element was provided in the Supplementary Figure 3.

Figure 2. SEM results of (A) S-1, (B) S-2, (C) S-3, (D) S-4, (E) S-5 and (F-K) EDS results for S-5.

XPS was used to analyze the valence states of elements in S-5. As shown in Figure 3, Cu 2p showed two peaks at 931.4 and 951.3 eV [Figure 3A], corresponding to the valence state of Cu^+[19]. The Mn 2p_3/2 binding energy peak was observed at 640.8 eV, while the Mn 2p_1/2 peak was observed at 653.3 eV [Figure 3B], which is also the case in Cu₂MnSnSe₄^[19] and XPS study of Mn^2+[32]. It can be concluded that the valence state of Mn in the sample is +2. Sn 3d_5/2 and Sn 3d_3/2 binding energy peaks were observed at 485.8 and 494.5 eV, respectively [Figure 3C], with no other significant peaks. In Cu₂ZnSnSe₄^[33], the binding energy peak of Sn 3d_5/2 is about 486 eV, indicating that Sn shows +4 valence. The Se 3d showed two peaks at 54 and 59.2 eV [Figure 3D], corresponding to the valence state of Se^2-[16,30]. Comparison of the Se XPS peaks for the S-2 and S-5 samples and find that the peak shift observed in the S-5 sample [Supplementary Figure 4] proves the successful doping of Te. Supplementary Figure 1 further supports this conclusion. As for the measurement of the valence state of Te, due to the low content of Te in the sample, the Te signal is easily obscured by background noise during the XPS measurement, resulting in an indistinct peak shape. However, the above results from local amplifications of the XRD patterns [Supplementary Figure 1] and XPS have indicated the presence of Te^2-.

Figure 3. X-ray photoelectron spectroscopy of S-5: (A) Cu 2p (B) Mn 2p (C) Sn 3d (D) Se 3d.

Figure 4 shows the electrical performance measurement results of all samples. At 473 K, the σ of all samples reached its maximum value. Specifically, the σ for S-2 is 4.27 × 10⁴ S m^-1, and for S-5, it is 1.56 × 10⁴ S m^-1 at 473 K [Figure 4A]. At around 470 K, the σ shows a non-monotonic change; unlike the decrease in σ at high temperatures caused by thermally activated charge carriers in some functional materials^[34], this change in conductivity behavior may be due to the transition from Cu ordered state to Cu disordered state^[16]. With the doping of Te, the sample conductivity decreases continuously. Hall effect test at room temperature [Figure 4B] was conducted to determine the reason for the change in conductivity. The heterovalent substitution of Mn by Cu in S-2 led to an increase in both n_H and μ_H; the n_H of S-2 is significantly increased compared to that of the S-1 sample (from 1.66 to 3.38 cm^-3), resulting in an enhancement in conductivity. With the doping of Te, the n_H of the samples (S-3 to S-5) fluctuates in the range of 4.1 × 10¹⁹ and 3.9 × 10¹⁹ cm^-3, according to the findings of Zhang et al., in Cu_2.1Mn_0.9SnSe₄, the Cu vacancy defect is the main defect, so it is speculated that the fluctuation of n_H is due to the change of Cu vacancy concentration caused by Te doping^[26]. Following Te doping, the μ_H of the sample decreases, primarily due to an increase in point defects; the scattering centers are formed within the material, which scatters the movement of the carrier, thus reducing the μ_H.

Figure 4. Temperature dependences of (A) the electrical conductivity (σ), (C) the Seebeck coefficient (S) and (D) the power factor (PF) for all samples. (B) the room temperature Hall carrier concentration (n_H) and mobility (μ_H) for all samples.

Figure 4C illustrates the relationship between the Seebeck coefficients (S) and temperature. All S exhibit positive values, suggesting that holes serve as the primary charge carriers. The S values of S-2 to S-5 are lower than those of S-1, due to the increase of n_H. At 673 K, S-5 obtains a maximum S of 219 μV K^-1 in the doped sample. The PF of each sample was calculated using PF = S²σ, and the temperature dependence of each sample’s PF was shown in Figure 4D. The PF of all the samples showed a monotonic temperature dependence, with the PF increasing with the temperature. At 673 K, the doped samples exhibit a higher PF compared to the undoped samples. In the low-temperature region (less than 450 K), the PF of S-2 to S-4 was almost the same, while the PF of S-5 remained high. With the temperature increase, the PF of S-2 further rises, reaching a maximum of 663 μW m^-1 K^-2 at 673 K. The temperature dependence of the PF of S-2 and S-3 is nearly identical, except at 623 K.

Figure 5A shows that the κ_tot of the samples exhibits a decreasing trend throughout the measured temperature range (consistent with the trend of changes in the thermal diffusivity coefficient (D), Supplementary Figure 5). In non-stoichiometric sample (S-2), as the Te doping content increases (S-3 to S-5), the κ_tot is greatly reduced in the low-temperature region (below 450 K), and the decline slows down in the high-temperature region (above 450 K). For example, κ_tot decreases from 2.89 W m^-1K^-1 of S-2 to 1.92 W m^-1K^-1 of S-5 at 323 K, a reduction of 0.97 W m^-1K^-1. Similarly, it decreases from 1.16 W m^-1K^-1 of S-2 to 0.75 W m^-1K^-1 of S-5 at 673 K, a reduction of 0.41 W m^-1K^-1. At 323 K, S-5 achieved a minimum κ_tot of 1.92 W m^-1K^-1, and at 673 K, it reached 0.75 W m^-1K^-1. The Wiedemann-Franz formula can be utilized to compute the electron thermal conductivity (κ_e = LσT, Supplementary Figure 6). As shown in Figure 5A, the κ_e increases first and then decreases within the measured temperature region. At 523 K, S-5 achieves a peak κ_e of 0.14 W m^-1K^-1, which decreases to 0.12 W m^-1K^-1 at 673 K. It is clear that the contribution of the κ_e to the κ_tot is very small. The κ_L of the samples can be obtained by κ_L = κ_tot - κ_e [Figure 5B]. At 323 K, S-5 exhibits a κ_L of 1.9 W m^-1K^-1, which is about 34% lower than that of S-2. Finally, S-5 exhibits the lowest κ_L of 0.6 W m^-1K^-1 at 673 K across the entire measured temperature region, which is a low level among some quaternary chalcogenides^{[16,21,35,36]}. Within the entire measured temperature range, the κ_L decreases by 25% to 30%, suggesting that within a certain defect concentration range, the κ_L decreases as the defect concentration increases.

Figure 5. The dependence of various thermal conductivity on temperature for all samples: (A) the total thermal conductivity (κ_tot) and electron thermal conductivity (κ_e), (B) the lattice thermal conductivity (κ_L) for all samples. (C) The theoretical κ_L of S-5 calculated based on Debye-Callaway model. (D) The total disorder parameter (Γ), the mass fluctuation parameter (Γ_M) and strain field fluctuation parameter (Γ_S) for all samples.

To further explore the reasons for the change of thermal conductivity, ultrasonic measurement was conducted on all samples, and the results are shown in Table 2. The average sound velocity (v_a), Grüneisen parameter (γ), mean free path of phonons (l_ph), the heat capacity (C_p) and Debye temperature (θ_D) were calculated for all samples (the relevant calculation details are shown in Supplementary Material). It is evident from Table 2 that the v_a of all samples remains nearly constant, and the heat capacity remains unchanged at 0.32 J g^-1 K^-1. According to l_ph = 3κ_L/ρC_pυ_a, the κ_L decreases mainly due to the reduction of l_ph. S-2 and S-3 have the same l_ph. Observing from Figure 5B, it is evident that the κ_L for S-2 and S-3 displays a similar trend of variation. As Te continues to rise, the l_ph of S-4 and S-5 diminishes, resulting in a decrease in κ_L. This suggests that the scattering effect of defects on phonons becomes increasingly pronounced, thereby contributing to the reduction in κ_L. S-5 has the shortest l_ph (1.68 nm).

Theoretical simulations of the experimental κ_L were conducted using the Debye-Callaway model, with phonon-phonon Umklapp scattering (U), Normal scattering (N), grain boundary scattering (GB) and point defects scattering (PD) as the primary scattering mechanisms. In the Debye-Callaway model, the κ_L of a material can be expressed as:

Phonon relaxation time is the result of multiple scattering mechanisms, which can be expressed as:

where k_B is the Boltzmann constant; $$\hbar$$ is Planck’s constant; ω is the phonon frequency; τ_c is the relaxation time (the relevant calculation details are shown in Supplementary Material). The existence of phase transitions in the samples may affect the propagation speed and scattering probability of phonons, so the experimental data were fitted in segments. Taking S-5 as an example, a theoretical simulation of the experimental κ_L was conducted through the Debye model [Figure 5C]. In the low-temperature region (less than 450 K), the experimental results for S-5 align well with the green dashed line (U + N + GB), indicating that U, N, and GB are the primary scattering mechanisms in this temperature range. In the higher-temperature region (more than 450 K), the experimental results for S-5 align well with the orange dashed line (U + N + GB + PD), suggesting that point defect scattering gradually becomes one of the main scattering mechanisms. By directly comparing the four different dashed lines, it is noticeable that point defects significantly contribute to the decrease in κ_L.

With the increase of defect concentration, the mass and strain field fluctuations will be further induced, which will affect the total disorder of the crystal. Γ = Γ_M + Γ_S, where Γ is the total disorder parameter, Γ_M is the mass fluctuation parameter and Γ_S is the strain field fluctuation parameter (the relevant calculation details of Γ_M and Γ_S are shown in Supplementary Material). Figure 5D illustrates the variation of the mass fluctuation parameter and the strain field fluctuation parameter. It is evident that both Γ_M and Γ_S increase with the Te, and for each set of samples, the value of Γ_S exceeds Γ_M, suggesting that the strain field fluctuation scattering make the primary contribution to reducing κ_L. Since the atomic radius of Te is larger than that of Se, the substitution of Se by Te leads to deviations in atomic positions and thus increasing local lattice distortions. This is the main reason for why Γ_S is greater than Γ_M. In conclusion, these factors can well explain the contribution of point defects to the decrease of κ_L.

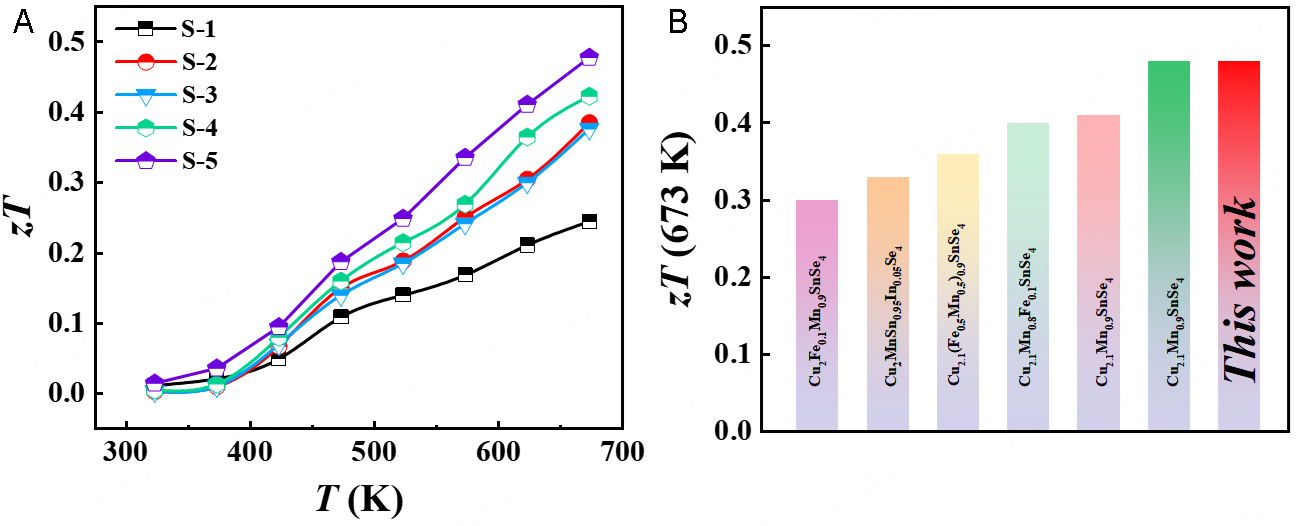
The relationship between the zT and temperature is shown in Figure 6A. After Te doping, zT is significantly enhanced throughout the measured temperature range due to the optimized PF and low κ_L. Finally, S-5 achieves the maximum zT ~ 0.5 at 673 K, roughly twice that of the S-1. Supplementary Figure 7 compares the thermoelectric properties between Cu_2.1Mn_0.9SnSe_3.9Te_0.2 and Cu_2.1Mn_0.9SnSe_3.9Te_0.1 [Supplementary Figure 7]. The results indicate that, within the Cu_2.1Mn_0.9SnSe_4-xTe_xsamples, the compound with x = 0.1 exhibits the optimal thermoelectric performance. Figure 6B presents the maximum zT achieved by some other Cu₂MnSnSe₄ systems at 673 K. This work attained a relatively high zT among Cu₂MnSnSe₄ systems, as can be easily observed.

Figure 6. (A) Temperature dependence of the dimensionless figure of merit (zT) for all the samples. (B) Comparison of zT for S-5 and other Cu₂MnSnSe₄ systems^{[21,27-29,37,38]} at 673 K.

CONCLUSIONS

In this work, a series of samples, including Cu₂MnSnSe₄ (S-1) and Cu_2.1Mn_0.9SnSe_4-xTe_x (x = 0,0.01,0.05,0.10; S-2 to S-5), were successfully synthesized by ball-milling and hot-pressing methods, and their structural components and electrothermal transport properties were studied. Rietveld refinement and SEM showed that all samples are tetragonal stannite structures with high density. XPS showed that Te doping does not change the valence states of the sample elements. The increase of n_H leads to elevation of the σ in S-5, and the PF of S-5 reaches 530 μW m^-1 K^-2 at 673 K. As the doping content of Te increases, the defect concentration in the samples also rises, resulting in enhanced scattering effects on phonons, thus reducing the l_ph and hindering phonon transport, which significantly reduces the κ_L. At 673 K, S-5 reaches a minimum κ_L of 0.62 W m^-1 K^-1. Due to the improvement of PF and the decrease of κ_L, S-5 reaches zT ~ 0.5, which is about twice that of the S-1 at 673 K. Therefore, it can be shown that the introduction of Te can further improve the thermoelectric performance of Cu₂MnSnSe₄-based compounds.