The application of phase-field method in magnetoelastic functional materials
Abstract
The phase-field method has become a powerful tool in materials science and engineering, providing a strong framework to understand phase transitions and microstructure evolution. By connecting atomic-scale phenomena to macroscopic behavior via mesoscale modeling, it has greatly enhanced our understanding of material processes. This paper presents micromagnetic microelastic phase-field modeling and explores recent applications of this approach in studying microstructural evolution and ultrasensitive magnetoelastic responses at phase boundaries in magnetoelastic functional materials, including magnetostrictive compounds and ferromagnetic shape memory alloys. The paper also discusses significant advances in phase-field modeling of magnetoelastic-electric coupling in multiferroic systems and magnetoelectric heterostructures. Finally, we identify key challenges and future directions for the phase-field method to advance the development of magnetoelastic functional materials.
Keywords
INTRODUCTION
The properties of materials at phase transitions - mechanical, electrical, and magnetic - are influenced not only by their chemical composition but also by the arrangement of microstructures and the distribution of defects[1,2]. The phase-field method eliminates the need for predefined microstructural configurations using a diffuse-interface technique to define phases or grain boundaries[3,4]. This approach allows for the simultaneous consideration of various fields - chemical, thermal, mechanical, magnetic, and electrical - capturing the dynamic interplay of internal and external forces that drive microstructural evolution and material properties. Consequently, the phase-field method has become a crucial analytical tool for understanding the complexities of phase transitions and the evolution of microstructures in materials science and engineering.
Originally, the term "phase-field" was invented to refer to phase transition problems in physics and was initially used to describe the transition process between the solid and liquid phases, in order to avoid tracking interfaces in solidification modeling[5]. The phase-field method, as a tool for describing continuous phase changes in a system, particularly at infinitesimal scales, provides an effective mathematical framework for describing phase transition dynamics and interface evolution. Since the 1990s, the maturation of the phase-field model coupled with advancements in computational technology, has resulted in substantial progress in the application of phase-field methods. Several review articles and textbooks regarding the phase-field method are now available[6-15]. To date, the phase-field simulation has been extensively used in various fields, including solidification[16-18], crystal growth[19-22], nucleation[23], coherent precipitate coarsening[24-26], dislocation[27,28], cracking[29], corrosion[30,31], batteries[32], martensitic transformations[33-36], ferroelectrics[37,38], ferromagnetics[39,40] and composites[41,42].
The phase-field method is essentially a numerical approach based on continuum theory, which avoids the complexity of directly tracking interfaces during the evolution of interfaces and phase transitions. It characterizes the thermodynamics of a material's microstructure by using its total free energy, represented as a functional that considers the spatial distribution of morphological features. Phase-field methods provide the benefit of examining specific types of energy contributions independently to understand their unique importance to the evolution of a mesoscale structure. The spatial arrangement of morphological features is captured by continuous state variables, known as "phase-field" variables or order parameters[43,44]. These variables can take on different values at various points within the material, signifying the presence of distinct phases or structural morphologies. Phase-field variables are classified into two categories based on the temporal and spatial evolution of the order-parameter field during microstructural development: (i) Conservative field variables, which maintain a constant total quantity throughout the microstructural evolution, such as atomic concentration fields and charge concentration fields; and (ii) Non-conservative field variables, which do not conserve their total quantity and can fluctuate, exemplified by the polarization field in ferroelectric materials, the magnetization field in ferromagnetic materials, and the orientation field describing the martensitic phase transformation in metallic materials. The Cahn-Hilliard dynamic equation is commonly used for conservative field variables to describe diffusional phase transitions[45,46]. On the other hand, non-conservative field variables are characterized by the Allen-Cahn dynamics, commonly referred to as the Time Dependent Ginzburg-Landau (TDGL) equations[47,48]. The evolution of the microstructure of materials can be elucidated by obtaining the spatial and temporal evolution of field variables through solving the phase-field equations, which in turn allows for the identification of the inhomogeneous components and structural phase fields within the material at various time intervals.
Magnetoelastic functional materials, which facilitate the coupling of strain and magnetization, are essential for the functioning of actuators and sensors in various precision control applications[49-52]. One notable example is the giant magnetostrictive material branded as Terfenol-D (TbxDy1-xFe2)[52], developed by the U.S. Naval Research Laboratory and the Navy Surface Weapons Center in the 1980s. Terfenol-D has since been applied in submarine sonar systems and spacecraft radar. More recently, another magnetostrictive material, Galfenol (Fe-Ga), has found applications in medical fields, including remote cell actuation and bone repair[53,54]. These examples highlight the significant potential of magnetoelastic functional materials in both military and civilian high-tech fields. As such, it is crucial to study these materials from a deeper microscopic mechanism perspective to achieve a large and low/nonhysteretic magnetoelastic response. However, magnetoelastic coupling often involves complex nonlinear dynamics that have historically been neglected in conventional micromagnetic simulations. This neglect can lead to significant inaccuracies, particularly when analyzing complex magnetic domain configurations under nonuniform magnetic fields. It is especially pronounced in materials with high magnetostriction, where overlooking magnetoelastic coupling can result in substantial errors. This underscores the need for advanced models that account for magnetoelastic interactions to enhance the accuracy of micromagnetic simulations and, consequently, the performance of precision control devices. The elastic strain field, which plays a crucial role in magnetoelastic materials, can be integrated with other field variables to manipulate the microstructure and properties of these materials under multiphysical fields. Traditional constitutive mechanical models generally describe material behavior through the macroscopic response, whereas the phase-field method, by introducing microscopic-scale elastic strain phase-field variables, allows for a more precise simulation of complex material behaviors. The coupling of phase-field methods with constitutive models enables the consideration of microstructural influences when describing the macroscopic mechanical behavior of materials. For instance, by combining phase-field evolution with constitutive models for plasticity, elasticity, and other properties, it becomes possible to predict the macroscopic response of materials under stress with greater accuracy.
This article presents recent phase-field simulation results related to phase transformations and microstructural evolution in magnetic functional materials, focusing on magnetostrictive alloys and magnetic shape memory alloys. The simulations utilize micromagnetic microelastic phase-field modeling applied to magnetoelastic coupled systems. These results, representing a decade of work by the authors and other researchers, exemplify the application of this modeling approach. Special attention is paid to the effects of phase transformations and the intricate evolution of microstructures under multiple physical fields on material properties, along with strategies for guiding microstructural evolution. The development and application of electro-elastic-magnetic coupling phase-field models in magnetoelectric (ME) heterojunction structures will also be discussed. In conclusion, a comprehensive summary and future outlook on the use of phase-field simulations for magnetic functional materials will be provided.
MICROMAGNETIC-MICROELASTIC PHASE-FIELD MODELING
In order to model the temporal evolution of the magnetic domain configuration in magnetoelastic functional materials, three key order parameters are typically utilized. The initial parameter represents the spatial arrangement of the spontaneous magnetization M(mi), with mi (i = x, y, z) denoting the normalized magnitude of magnetization vector along the Cartesian coordinates. The second parameter encompasses the local strain distribution ε(r), which is employed to characterize the different structural variants. The total free energy of a magneto-elastic functional material could be expressed as[55-57]
where Eani, Eexc, Ems, Eel, Egrad, and Eex represent the energy densities of magnetocrystalline anisotropy energy, magnetic exchange energy, magnetostatic energy, elastic energy, gradient energy and external magnetic energy, respectively.
The energy associated with magnetocrystalline anisotropy arises from the spin-orbit coupling and is considered an inherent material characteristic. For cubic systems, this energy density can be expressed as[58-60]
where K1 and K2 are the magnetocrystalline anisotropy coefficients with a unit of J/m3.
The exchange energy promotes the alignment of neighboring magnetizations, a behavior governed by the spatial dependence of the magnetization direction. The exchange energy density is[57-60]
where A denotes the exchange stiffness constant with a unit of J/m.
Magnetostatics energy represents the interaction of the magnetic body's own magnetization with the demagnetizing field it generates. The corresponding energy density may be formulated as[56,60]
where µ0 is vacuum permeability with a unit of H/m, and Ms is the saturation magnetization, with a unit of A/m. Hddenotes the demagnetization field determined by the shape of magnetic materials, and it could be obtained by solving the magnetostatic equilibrium equation ∇·(µ0Hd+ µ0Msm) = 0.
The energy associated with mechanical strain within the material can be articulated in terms of elastic energy, and the elastic energy density is given by[56,60]
where cijkl signifies the elastic stiffness tensor, which is a fourth-rank tensor characterizing the material's resistance to deformation. The stress-free strains
The strain gradient energy, which accounts for the energy associated with the variation of the strain field, is incorporated via the gradients of the strain order parameter. This energy density term is instrumental in characterizing the interfacial energy that is inherently linked to twin boundaries[62]
where g represents the gradient energy coefficient, which quantifies the energy contribution due to the spatial inhomogeneity of the strain field.
The influence of an external applied magnetic field Hexis incorporated by considering the interaction between magnetization and the external field[57,58,60]
The functional derivative of the total energy Etot with respect to the local magnetization yields the expression for the effective field, which is given by
where α denotes the Gilbert damping parameter, while γ0 signifies the gyromagnetic ratio. The dynamics of the local magnetization can be numerically addressed by employing the Gauss-Seidel iterative projection technique, as referenced in Ref.[63]. The equation can be discretized in time using the dimensionless parameter
The temporal and spatial evolution of stress-free strain can be articulated through the time dependent Ginzburg-Landau (TDGL) equation
where L refers to the kinetic coefficient. The numerical resolution of the equation can be effectively achieved by employing the semi-implicit Fourier-spectral method, as detailed in Ref.[64].
In the case of polycrystalline magnetic materials, we establish a universal global coordinate system applicable to all grains. We describe the orientation of a particular grain in the polycrystalline structure using three Euler angles (φ, θ, ψ), corresponding to three consecutive counter-clockwise rotations with respect to the global coordinates (x1, x2, x3): φ about the x3-axis, θ about the rotated x′1-axis and ψ about the newest x′3-axis. Consequently, the transformation matrix for converting from the global to the local coordinate system is provided by
The local magnetization vector
Here, Rij is the grain rotation matrix field that encapsulates the geometrical attributes (dimensions, morphology, and position) and the crystallographic orientation of the individual grains within the magnetic polycrystals.
THE APPLICATION OF PHASE-FIELD METHOD IN MAGNETOELASTIC FUNCTIONAL MATERIALS
Magnetostrictive materials
Giant magnetostriction and ferromagnetic MPB
Giant magnetostriction, characterized by a significant, reversible, and low/non-hysteretic change in strain under magnetic fields, is essential for the functionality of magnetostrictive materials in applications such as sensors, actuators, and transducers[49-52]. Over the past few decades, researchers have focused on developing an anisotropy compensation mechanism to reduce magnetic anisotropy, optimizing giant magnetostriction at low fields[66-69]. As shown in Figure 1, Newnham[70] initially recognized the spin reorientation transition in (Tb-Dy)Fe2 as analogous to the morphotropic phase boundary (MPB) in quasi-binary ferroelectric systems, a notion that was later substantiated by the work of Yang et al.[71] and Bergstrom et al.[72]. This recognition has prompted numerous research groups to conduct comprehensive studies on the ferromagnetic MPB[73-78], yielding significant findings such as the inverse MPB effect on magnetostriction and the concurrent presence of nanodomains of multiphases. Collectively, these investigations have substantially expanded our understanding of MPB phenomena and have paved the way for innovative approaches to the design of large magnetostrictive materials. Nonetheless, the granular dynamics of domain evolution and phase transitions at the MPB remain obscure, posing a significant scientific and technological challenge. The primary challenges are the intricate experimental observations required and the theoretical intricacies associated with the multiphase interplay near the ferromagnetic MPB.
Pre-transitional rhombohedral phase near ferromagnetic MPB
The ferromagnetic MPB provides a promising design strategy for achieving highly sensitive magnetoelastic responses. Current research, however, focuses on materials with rhombohedral structures, particularly
Figure 2. (A) Schematic of the eight <111> easy axes in the (Tb-Dy)Fe2 single crystals. (B) 3D domain structures of Terfenol-D[56]. (C) Dynamic evolution of 109° and 71° domain walls under external fields[85]. (D) Simulated magnetization (strain) responses and typical domain structures of twinned Terfenol-D crystal in three different cases: (i) non-interacting domains with magnetization rotation only; (ii) magnetically but not elastically interacting domains with both magnetization rotation and domain wall motion; and (iii) taking into account all energy contributions and allowing magnetization to evolve freely[40].
Engineered tetragonal phase near ferromagnetic MPB
The previous section demonstrated that the pre-transitional rhombohedral phase magnetic materials possess substantial intrinsic strain, which can contribute to giant magnetostriction. However, it is essential to recognize that reversible or hysteresis-free magnetostriction is critical for achieving precise control in magneto-mechanical applications. In their recent work, Xu et al. discovered that applying intermediate external magnetic fields along non-easy magnetic axes during the nucleation phase can substantially influence the subsequent growth and evolution dynamics of domains[86]. Notably, an engineered tetragonal crystal exhibited a giant and non-hysteretic magnetoelastic response [Figure 3A]. The authors suggested that domain wall broadening accounted for the notable enhancement in non-hysteretic magnetostriction. Additionally, a discernible correlation between domain wall densities and the applied fields was also provided to guide the development of engineered tetragonal crystals [Figure 3B]. Their study presents a fresh viewpoint by questioning the traditional assumption that considerable magnetostriction is solely limited to the rhombohedral phase region of the ferromagnetic MPB.
Figure 3. (A) Non-hysteretic magnetostriction responses for the engineered tetragonal phase near ferromagnetic MPB; (B) The relationship between the density of domain wall and the applied magnetic field along non-easy magnetic axes[86].
Domain microstructures and magnetostriction near ferromagnetic MPB
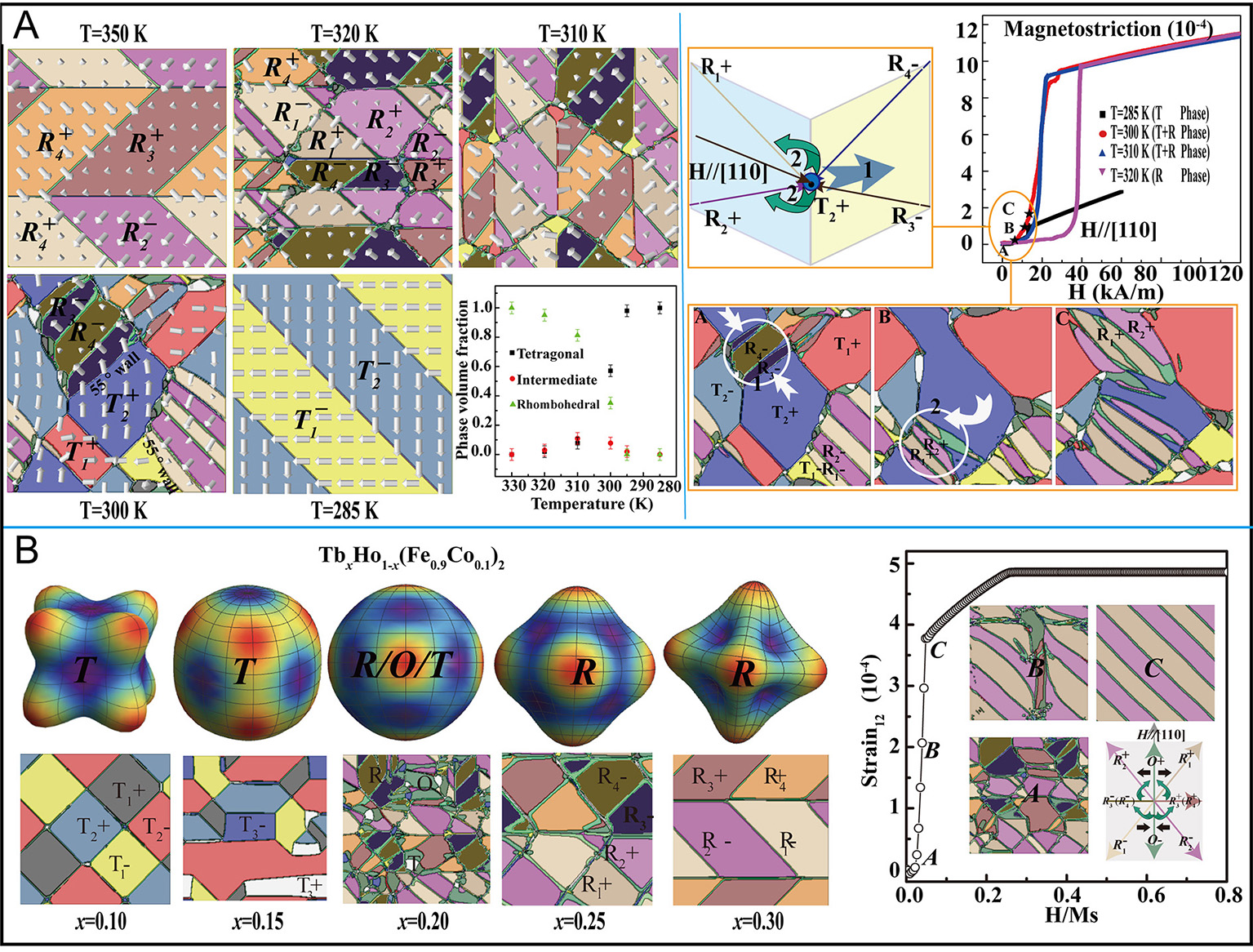
In ferromagnetic systems with MPBs, the microstructural characteristics near the critical region of phase coexistence are highly responsive to competing energy interactions. Perturbations, particularly thermal ones, can induce transitions between ferromagnetic phases, forming a thermal phase boundary known as the ferromagnetic thermotropic phase boundary. This boundary differs from its ferroelectric counterpart, characterized by a broadened region rather than a sharp line. Figure 4A depicts the domain evolution and magnetostriction in the Tb0.27Dy0.73Fe2 magnetostrictive system as it approaches this thermotropic boundary. Minor domain variants form at the intersections of rhombohedral domains, integrating with the main phase[87]. High-resolution transmission electron microscopy (HR-TEM) confirms the coexistence of these phases, with domain-averaged stress accommodating a metastable state highly reactive to external fields[88]. Domain variant transformations are facilitated by domain wall motion and switching, with the tetragonal phase acting as a low-energy conduit for rhombohedral domains to align with the applied field. Figure 4B illustrates complex domain dynamics near a composition-induced tricritical-type ferromagnetic phase boundary in the TbxHo1-x(Fe0.9Co0.1)2 system, where three phases - rhombohedral (R), orthorhombic (O), and tetragonal (T) - coexist and transition across a flat energy landscape[89]. The interplay of local energy minima and stress accommodation enhances multiphase stability. At low applied fields, a pronounced magnetostrictive response is evident, with the metastable O phase variants rapidly transitioning to the R structure in alignment with the external field. The presence of T and O phase traces serves as intermediate states, enabling low-energy domain reorientation. The considerable inherent strain of the rhombohedral phase, coupled with a broad, flat energy barrier, grants the system an exceptionally sensitive magnetoelastic response. Recently, Ke et al. offered convincing proof of magnetization rotation at the ferromagnetic MPB in the Tb1-xDyxFe2 system[90]. These series of works further experimentally demonstrate the crucial role of phase-field simulation methods in understanding the magnetoelastic mechanisms at the ferromagnetic MPB and in guiding the development of high-performance magnetoelastic functional materials.
Figure 4. Domain microstructure evolution and magnetostriction for (A) Tb0.27Dy0.73Fe2 near the temperature-induced ferromagnetic MPB[87] and (B) TbxHo1-x(Fe0.9Co0.1)2 near the composition-induced ferromagnetic MPB[89]. R/O/T are the abbreviations of three structural types (rhombohedral/orthorhombic/tetragonal) with different easy magnetization directions: R1+<1,1,1>, R1-:<-1,-1,-1>,
Polycrystalline and amorphous systems near ferromagnetic MPB
Unlike single crystals, polycrystalline materials possess an abundance of grain boundaries, where mutual extrusion can facilitate the nucleation and growth of new phases. Ke et al. investigated the effect of grain size on magnetostrictive polycrystals near the ferromagnetic MPB using micromagnetic and microelastic phase-field simulation techniques[90]. Figure 5A shows the phase coexistence and magnetoelastic behavior of TbxDy1-xFe2 nanocrystals. Their study revealed that grain nanocrystallization effectively broadens the ferromagnetic MPB. Furthermore, nanocrystalline materials consistently show low hysteresis and enhanced magnetostrictive sensitivity, with this effect becoming more pronounced as grain size decreases. This research offers theoretical insights for designing giant, anhysteretic magnetostrictive nanocrystalline materials. Importantly, the phase-field simulation results provide a theoretical approach for enhancing the performance of light rare-earth-based giant magnetostrictive materials, which cannot form single crystals or oriented crystals under ambient pressure. In a separate study, Dai et al. developed a graph neural network (GNN) machine learning model[91] to systematically investigate the effects of grain size, orientation, and other microstructural factors on the magnetostrictive response of Terfenol-D polycrystals [Figure 5B]. This microstructure-graph-based GNN model allows for accurate and interpretable predictions of the properties of polycrystalline materials. Moreover, this work provides a powerful exploration and guidance for the high-throughput development of polycrystalline magnetostrictive materials based on phase-field simulations.
Figure 5. (A) The grain configuration and grain size effect of phase coexistence and magnetoelastic response of Tb0.27Dy0.73Fe2 nanocrystals. (a) Grain size effect phase coexistence around ferromagnetic MPB. (b) Magnetostriction loops of different-sized nanocrystals. (c) Magnetization and domain structures of the polycrystals with different average grain sizes[90]. (B) Dataset of 3D microstructures of polycrystalline Tb0.3Dy0.7Fe2 and their effective magnetostriction. Distributions of (a) size (represented by the number of voxels), (b) the number of neighboring grains for a specific grain, and (c) three Euler angles of the 87,981 grains in the entire dataset of 492 microstructures. (d) An example of 3D polycrystalline microstructure in the dataset. (e) Local magnetization and (f) local magnetostriction on the 2D slice. (g) Effective magnetostriction of the 3D microstructure as a function of the applied magnetic field[91].
Sun et al. introduced a thermodynamically-consistent micromagnetic-mechanically coupled phase-field model[92] aimed at elucidating the fracture and fatigue mechanisms in amorphous Terfenol-D amorphous films. The model incorporates the evolution of micromagnetic structures and their intricate coupling with mechanical deformation, facilitating a comprehensive understanding of the material’s structural reliability under the influence of external magnetic fields. A thermodynamically consistent phase-field model[93] was developed by Rezaei et al. to elucidate the magnetic field-induced grain boundary migration in polycrystalline magnetic metals, revealing the impact of magnetic field parameters on microstructure and texture evolution[93].
Fe-Ga magnetostrictive materials
Compared with Tb-Dy-Fe magnetostrictive materials, Fe-Ga alloys have numerous advantages, including low cost, low switching field, high mechanical properties, etc. Fe-Ga alloys, first identified by Clark in 2000 as a significant class of magnetostrictive materials, display various structural configurations resulting from the complex interactions between Fe and Ga[93-97]. These structural variations profoundly influence both the magnetic properties and the thermodynamic stability and performance of the alloys under varying environmental conditions. To gain insights into the energetic factors affecting the formation and stability of complex magnetic domain structures, Zhang and Chen used an integrated approach that combines phase-field microelastic theory with micromagnetic simulations to model the evolution of magnetic domains in Fe-Ga alloys[56]. As depicted in Figure 6A, their analysis demonstrated that the alignment of 90° domain walls is primarily driven by the minimization of elastic energy, whereas the orientation of 180° domain walls is governed by magnetostatic energy. A key finding of their study showed that the subdivision of 180° domain walls is mainly induced by domain degeneracy with distinct magnetic easy axes, challenging the assumption that this behavior was dictated solely by elastic or magnetostatic interactions. They also conducted quantitative simulations to evaluate how pre-stress treatments commonly applied to Fe-Ga alloys influence their magnetostrictive properties. By employing polar and azimuthal angles (θ1, θ2) as the order parameters in place of the magnetization unit vector m, Yi and Xu developed a continuous, constraint-free phase-field model[98] to account for the domain evolution of FeGa under external magnetic and mechanical loadings.
Figure 6. (A) Domain evolution of Fe-Ga in the presence of both elastic energy and magnetostatic energy: (a) 4,000 steps; (b) 40,000 steps; (c) 200,000 steps; (d) 500,000 steps. (e) The field dependence of magnetostriction with different pre-stress applied[56]. (B) The matrix distortion along [100] direction with a parallel saturation magnetic field in (a) Fe-Ga and (b) Fe-Ga-La alloys, respectively. (c) Re-magnetization process along the easy axis direction. The re-magnetization is realized in Fe-Ga-La by domain wall motion rather than by domain rotation[99].
More recently, it was found that introducing rare earth impurities that interact with nanoscale inhomogeneities in the Fe-Ga system can lead to giant magnetostriction. He et al. developed a mesoscopic model using phase-field simulations [Figure 6B] to demonstrate that bulk tetragonal distortion is largely driven by nano-heterogeneities with aligned Ga-Ga pairs under an applied magnetic field[99]. This enhanced tetragonal distortion within the doped nano-heterogeneities induces further matrix distortion, significantly contributing to the observed magnetostrictive behavior. Yan et al. further conducted an in-depth synthesis of research on the impact of local chemical ordering (LCO) in Fe-Ga solid solutions on the material's magnetoelastic response, emphasizing its role as a frozen intermediate state during the A2 to L12 phase transformation[100].
Magnetic shape memory alloys (MSMAs)
Ferromagnetic shape memory alloys (FSMAs) have been widely studied for their multifunctional properties, including ferromagnetism and ferroelasticity, which result in complex interactions, particularly magnetic field-induced strain (MFIS)[101-105]. These alloys can exhibit significant strains in response to magnetic fields, making them promising candidates for applications in sensors and actuators. Despite considerable research on the mechanical and magnetic properties of Ni-Mn-Ga, the most studied FSMA, the mechanisms underlying its MFIS are still not fully understood. A comprehensive understanding of the intrinsic mechanisms driving MFIS in Ni-Mn-Ga requires examining the evolving microstructures, including domain arrangements and martensitic transformations. Zhang et al. introduced a pioneering phase-field model that integrates micromagnetics and microelasticity to simulate the complex behavior of FSMAs[101]. Their work accurately predicts the evolution of both magnetic domain structures and martensitic microstructures in response to applied magnetic fields, aligning with experimental observations.
Jin developed a phase-field micromagnetic microelastic model[106,107], demonstrating that the mobility of twin boundaries in magnetic shape memory alloys significantly influences the evolution of domain microstructures and the associated magnetomechanical responses, as illustrated in Figure 7A. This underscores the inherent complexity of domain phenomena in these materials. As illustrated in Figure 7B, Wu et al. employed phase-field simulations to investigate MFIS in the Ni2MnGa FSMA under various compressive stresses[108]. Their findings identified three distinct strain mechanisms and highlighted the significant influence of the martensitic microstructure on magnetization and strain evolution. Additionally, Peng et al. simulated magnetic hysteresis and mechanically induced remanent magnetization rotation in Ni-Mn-Ga, introducing a magnetic resistant field to quantify coercivity[109,110]. Their results indicate that mechanically induced demagnetization is a subset of magnetically and mechanically induced remanent magnetization rotation, as demonstrated in the simulation results presented in Figure 7C. Sun et al. developed a phase-field model to explore the microstructural evolution and thermomechanical properties of polycrystalline shape memory alloys, considering the effects of grain size, strain rate, and the release and conduction of latent heat during phase transformations, as shown in the numerical simulations depicted in Figure 7D[111]. Furthermore, Wu et al. created real-space-based phase-field simulation models to study the evolution of magnetic domain structures and twinning structures in shape memory alloys of arbitrary geometries[112]. More recently, Xu et al. used phase-field simulations to investigate the effects of variously shaped and sized pores on MFIS in the Ni2MnGa FSMA, revealing the critical role of pore orientation and size in tailoring the alloy's functional properties for advanced applications[113].
Figure 7. (A) Initial domain configuration of magnetic shape memory alloys (MSMAs) and their time evolution of magnetization and strain in three cases with varying twin boundary mobilities under a constant magnetic field[106]. (B) Schematic representation of the magneto-mechanical setup, along with the initial domain structure and martensitic microstructure of Ni2MnGa[108]. (C) Microstructural evolution of magnetically and mechanically induced remanent magnetization rotation in Ni-Mn-Ga alloys[109]. (D) Evolution of the microstructure in the polycrystalline nanowire of shape memory alloys during loading and unloading processes[111].
A general nanoembryonic mechanism model for supermagneoelastic response
Revisiting these typical magnetoelastic functional materials reveals that optimal magnetoelastic responses often occur at the phase transition boundaries, where two or three phases meet within the phase diagram. This observation raises the question of whether these materials have a generalized mechanism for supermagnetoelastic response.
Xu et al. introduced a nanoembryonic mechanism to explain the giant and anhysteretic magnetostrictions observed in pre-transitional materials[114]. This mechanism describes the process in highly defective pre-transitional materials, where local stresses from stress-concentrating defects, such as dislocations and nano-precipitates, create stable embryos of the product phase without thermal activation. These embryos exist in thermoelastic equilibrium with the parent phase. When an external magnetic field is applied, this equilibrium is disrupted, leading to a change in the volume fraction of the embryos[115]. Consequently, a substantial and hysteresis-free magnetoelastic response occurs, enhancing device sensitivity and efficiency. As illustrated in Figure 8A-C, their work systematically discusses the evolution of the nanoembryonic phase under quasi-static cyclic external fields at varying defect densities, along with the corresponding longitudinal strain responses. Furthermore, by correlating the formation of nanoembryos with the unique characteristics of ferromagnetic MPBs, the nanoembryonic mechanism model provides a unifying framework for understanding the exceptional properties observed in MPB systems, as shown in Figure 8D. This general nanoembryonic mechanism, encompassing superelasticity, elastic softening, and invar/elinvar effects, has broad implications for designing smart materials suitable for applications in sensors, actuators, and other advanced technologies.
Figure 8. (A) Free energy and domain evolution path around the MPB: (a) rhombohedral side and (b) tetragonal side. (B) Dislocation structures in pre-transitional materials prior to the formation of embryos. The estimated dislocation densities are generated from randomly placed Frank-Read sources under uniaxial stress. (C) The sequence of embryonic microstructures under a quasi-static cycling magnetic field. The different orientations of embryo variants are colored red, green, and blue, respectively. (D) Longitudinal strain responses to a quasi-static cycling magnetic field[115].
Magnetostrictive multiferroics: strain as the link
Building on foundational work in magnetoelastic materials, researchers have extended phase-field simulations to explore the complex behaviors of multiferroic systems. Early theoretical investigations by Nan explored the ME effect in composites made of piezoelectric and piezomagnetic phases, establishing a generalized framework for treating the coupled ME behavior[116]. This work laid the groundwork for designing composite materials with tailored ME properties. Srinivas and Li developed a self-consistent approach to calculate the macroscopic ME coefficients of polycrystalline multiferroic composites, revealing the significant effects of particle shape, volume fraction, and orientation distribution on ME coupling[117]. Ramesh and Spaldin provided a comprehensive overview of advancements in multiferroics, emphasizing the significance of strain-induced ME coupling in thin films[118]. These theoretical investigations have laid the foundation for understanding the strain-mediated interactions between magnetostrictive and electrostrictive phases in multiferroic materials, facilitating the simulation of microstructural evolution and domain dynamics via phase-field modeling.
Ni and Khachaturyan introduced a phase-field approach to investigate the strain-induced ME effect in piezoelectric-piezomagnetic multiferroic composites[119]. Their findings revealed that a plate-like configuration of phases results in the strongest ME coupling. Zhang et al. developed a phase-field model to examine ME coupling in epitaxial ferroelectric and magnetic nanocomposite thin films, considering various factors such as domain structures, electrostrictive effects, and substrate constraints[120]. Building upon this, Wu et al. employed a phase-field model to investigate the domain structures of ferroelectric particles embedded in a ferromagnetic matrix, examining the influence of particle size, shape, and the surrounding magnetic matrix on the stability of vortex structures[121]. Their study revealed that small ferroelectric particles form single-vortex structures with the potential to modulate ME coupling coefficients.
Additionally, Hu et al. utilized phase-field simulations to investigate strain-induced magnetic domain switching in epitaxial CoFe2O4 thin films, uncovering a pronounced difference in switching dynamics between single-domain and multidomain configurations under in-plane elastic strains[122]. Further expanding the understanding of ME heterostructures, Yang et al. established a magneto-electric-elastic coupled phase-field model to investigate the local elastic coupling between magnetic and ferroelectric domains in a multiferroic layered heterostructure of Co0.4Fe0.6/BaTiO3[123]. Their findings showed that the dynamic evolution of magnetic domains driven by electric fields occurs as a series of alternating local magnetization rotations and coupled movements of magnetic and ferroelectric domain walls.
CONCLUSIONS
The phase-field method has been widely applied to simulate the evolution of microstructures in various types of materials, involving a very diverse range of physical phenomena or processes, including solid-state phase transformations, solidification, grain coarsening and growth, crack propagation, and dislocation motion, etc. This work introduces the application of the phase-field method in magnetostrictive functional materials, focusing on microstructural evolution near the phase boundaries of RFe2 giant magnetostrictive materials, FeGa, and NiMnGa shape memory alloys, and its impact on magnetoelastic properties. These magnetoelastic materials typically exist in a quasi-equilibrium magneto-elastic-thermal state near phase boundaries, resulting in complex microstructures with multiple coexisting structural variants. Micromagnetic microelastic phase-field simulations can replicate experimental observations, quantify various energy contributions, and offer strategies for designing improved magnetostrictive materials. Additionally, strain elastic energy can serve as a medium for phase-field simulations of ME coupling in multiferroic systems.
The phase-field method is on the cusp of significant expansion, now covering most forms of organization and microstructural evolution in condensed matter. Looking ahead, several key areas emerge as crucial for advancing the phase-field method in materials science and engineering:
(i) The construction of phase-field models that incorporate the intrinsic characteristics of real materials. While phase-field simulations have adeptly captured the mesoscale microstructures of single crystal materials, which possess an inherent simplicity in their lattice structure, the extension to materials replete with defects - such as dislocations, vacancies, and grain boundaries - presents a significant challenge. Advancing phase-field models to encompass these defects is not only essential for a comprehensive understanding of their influence on material properties but also pivotal for the optimization of microstructures aimed at performance enhancement through defect engineering.
(ii) The development of phase-field simulation algorithms. Given that phase-field simulations necessitate the resolution of a complex system of coupled nonlinear partial differential equations, the computational demands can be exceedingly onerous. The pursuit of novel numerical methods that facilitate expedited yet accurate kinetic phase-field simulations is imperative, offering the potential to markedly reduce computational expenditures and tackle larger-scale problems.
(iii) The full process linkage of material development in phase-field simulations. Currently, phase-field researchers tend to focus on specific topics such as solidification, solid-state transformations, or device fabrication. There is often little exchange of insights between these areas, particularly regarding the interaction between preparation stages (e.g., solidification) and material functionality (e.g., responses to electromagnetic or elastic stimuli). Structural material researchers often focus on preparation intricacies, while functional material researchers emphasize characterization outcomes. This divergence can hinder accurate determination of thermodynamic free energy constants, which is critical for phase-field model accuracy. Despite the challenges, linking phase-field methods for structural and functional materials is highly valuable. Establishing such a link would significantly strengthen material development and design principles. This integrated perspective is essential for realizing the full potential of phase-field models and driving innovation in material science.
(iv) The establishment of a phase-field simulation database. With the rise of AI for Science, machine learning depends on large, high-quality datasets for training. High-throughput phase-field simulations can generate these datasets, streamlining material development.
The future of phase-field research promises substantial contributions to materials science by enhancing model realism, improving computational efficiency, fostering integration across development stages, and embracing data-driven approaches. These advances will solidify the phase-field method as an indispensable tool, enabling the design and discovery of new materials with tailored properties for numerous applications.
DECLARATIONS
Acknowledgments
We are very grateful for the productive discussion with Mr. Hong-Xian Li, the chairman of Liaocheng Guanxian Shang'ao Superhard Materials Co., Ltd. We would also like to express our gratitude to the Liaocheng "Vice President of Science and Technology" Collaborative Innovation Project.
Authors’ contributions
Conception and design of the study, supervision: Hu, C. C; Zhang, Z.
Data analysis and interpretation: Cai, T. T.; Xu, Y. X.; Zhang, S.; Huang, H. H.
Manuscript writing and revising: Cai, T. T.; Xu, Y. X.; Zhang, Z.; Zhang, S.
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work was financially supported by the Science Foundation of Shandong Province, China (No. ZR2022ME030), National Natural Science Foundation of China (No. 52301088), Science Foundation of Shandong Province, China (No. ZR2024ME201), Research Foundation of Liaocheng University (No. 318012119), and Liaocheng "Vice President of Science and Technology" Collaborative Innovation Project (No. 2024XT05).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Janssens, K. G. F.; Raabe, D.; Kozeschnik, E.; Miodownik, M.; Nestler, B. Computational materials engineering: an introduction to microstructure evolution. Burlington: Elsevier Academic Press; 2007. Available from: https://www.sciencedirect.com/book/9780123694683/computational-materials-engineering [Last accessed on 25 Apr 2025]
2. Bulatov, V. V.; Cai, W. Computer simulations of dislocations. New York: Oxford University Press; 2006, pp. 241.
3. Ginzburg, V. L.; Landau, L. D. 73 - On the theory of superconductivity. In: Collected Papers of L.D. Landau; 1965, pp. 546-68.
4. Cahn, J. W.; Hilliard, J. E. Free energy of a nonuniform system. I. interfacial free energy. J. Chem. Phys. 1958, 28, 258-67.
5. Collins, J. B.; Levine, H. Diffuse interface model of diffusion-limited crystal growth. Phys. Rev. B. Condens. Matter. 1985, 31, 6119-22.
6. Emmerich, H. The diffuse interface approach in materials science: thermodynamic concepts and applications of phase-field models. New York: Springer; 2003.
7. Chen, L.; Moelans, N. Phase-field method of materials microstructures and properties. MRS. Bull. 2024, 49, 551-5.
8. Zhao, Y. Understanding and design of metallic alloys guided by phase-field simulations. NPJ. Comput. Mater. 2023, 9, 1038.
9. Zhuang, X.; Zhou, S.; Huynh, G.; Areias, P.; Rabczuk, T. Phase field modeling and computer implementation: a review. Eng. Fract. Mech. 2022, 262, 108234.
10. Tourret, D.; Liu, H.; Llorca, J. Phase-field modeling of microstructure evolution: recent applications, perspectives and challenges. Prog. Mater. Sci. 2022, 123, 100810.
11. Tonks, M. R.; Aagesen, L. K. The phase field method: mesoscale simulation aiding material discovery. Annu. Rev. Mater. Res. 2019, 49, 79-102.
12. Emmerich, H. Advances of and by phase-field modelling in condensed-matter physics. Adv. Phys. 2008, 57, 1-87.
13. Boettinger, W. J.; Warren, J. A.; Beckermann, C.; Karma, A. Phase-field simulation of solidification. Annu. Rev. Mater. Res. 2002, 32, 163-94.
14. Chen, L. Phase-field models for microstructure evolution. Annu. Rev. Mater. Res. 2002, 32, 113-40.
16. Wang, F.; Altschuh, P.; Matz, A. M.; et al. Phase-field study on the growth of magnesium silicide occasioned by reactive diffusion on the surface of Si-foams. Acta. Mater. 2019, 170, 138-54.
17. Uddagiri, M.; Tegeler, M.; Steinbach, I. Interface stabilization and propagation in phase field models of solidification: resolving the issue of large driving forces. Model. Simul. Mater. Sci. Eng. 2024, 32, 065034.
18. Cai, Y.; Wang, F.; Czerny, A.; Seifert, H. J.; Nestler, B. Phase-field investigation on the microstructural evolution of eutectic transformation and four-phase reaction in Mo-Si-Ti system. Acta. Mater. 2023, 258, 119178.
19. Chen, L. Q.; Yang, W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: the grain-growth kinetics. Phys. Rev. B. Condens. Matter. 1994, 50, 15752-6.
20. Kobayashi, R.; Warren, J. A.; Craig, C. W. A continuum model of grain boundaries. Phys. D. 2000, 140, 141-50.
21. Iii C, Chen L. Computer simulation of 3-D grain growth using a phase-field model. Acta. Mater. 2002, 50, 3059-75.
22. Moelans, N.; Blanpain, B.; Wollants, P. Quantitative analysis of grain boundary properties in a generalized phase field model for grain growth in anisotropic systems. Phys. Rev. B. 2008, 78, 024113.
23. Gránásy, L.; Tóth, G. I.; Warren, J. A.; et al. Phase-field modeling of crystal nucleation in undercooled liquids - A review. Prog. Mater. Sci. 2019, 106, 100569.
24. Wang, Y.; Chen, L.; Khachaturyan, A. Kinetics of strain-induced morphological transformation in cubic alloys with a miscibility gap. Acta. Metall. Mater. 1993, 41, 279-96.
25. Zhu, J.; Wang, T.; Ardell, A.; Zhou, S.; Liu, Z.; Chen, L. Three-dimensional phase-field simulations of coarsening kinetics of γ′ particles in binary Ni-Al alloys. Acta. Mater. 2004, 52, 2837-45.
26. Liu, H.; Gao, Y.; Liu, J.; Zhu, Y.; Wang, Y.; Nie, J. A simulation study of the shape of β′ precipitates in Mg-Y and Mg-Gd alloys. Acta. Mater. 2013, 61, 453-66.
27. Zhao, Y.; Liu, K.; Zhang, H.; et al. Dislocation motion in plastic deformation of nano polycrystalline metal materials: a phase field crystal method study. Adv. Compos. Hybrid. Mater. 2022, 5, 2546-56.
28. Tian, X. L.; Zhao, Y. H.; Peng, D. W.; Guo, Q. W.; Guo, Z.; Hou, H. Phase-field crystal simulation of evolution of liquid pools in grain boundary pre-melting regions. Trans. Nonfer. Metal. Soc. China. 2021, 31, 1175-88.
29. Clayton, J.; Knap, J. Phase-field analysis of fracture-induced twinning in single crystals. Acta. Mater. 2013, 61, 5341-53.
30. Ansari, T. Q.; Xiao, Z.; Hu, S.; Li, Y.; Luo, J.; Shi, S. Phase-field model of pitting corrosion kinetics in metallic materials. NPJ. Comput. Mater. 2018, 4, 89.
31. Kovacevic, S.; Ali, W.; Martínez-Pañeda, E.; LLorca, J. Phase-field modeling of pitting and mechanically-assisted corrosion of Mg alloys for biomedical applications. Acta. Biomater. 2023, 164, 641-58.
32. Wang, Q.; Zhang, G.; Li, Y.; Hong, Z.; Wang, D.; Shi, S. Application of phase-field method in rechargeable batteries. NPJ. Comput. Mater. 2020, 6, 445.
33. Wang, Y.; Khachaturyan, A. G. Multi-scale phase field approach to martensitic transformations. Mater. Sci. Eng. A. 2006, 438-40, 55-63.
34. Wang, Y.; Khachaturyan, A. Three-dimensional field model and computer modeling of martensitic transformations. Acta. Mater. 1997, 45, 759-73.
35. Levitas, V. I.; Preston, D. L.; Lee, D. W. Three-dimensional Landau theory for multivariant stress-induced martensitic phase transformations. III. Alternative potentials, critical nuclei, kink solutions, and dislocation theory. Phys. Rev. B. 2003, 68, 134201.
36. Mamivand, M.; Zaeem, M. A.; El, K. H. A review on phase field modeling of martensitic phase transformation. Comput. Mater. Sci. 2013, 77, 304-11.
37. Wang, J.; Wang, B.; Chen, L. Understanding, predicting, and designing ferroelectric domain structures and switching guided by the phase-field method. Annu. Rev. Mater. Res. 2019, 49, 127-52.
38. Guo, C.; Huang, H. Design of super-elastic freestanding ferroelectric thin films guided by phase-field simulations. Microstructures 2022, 2, 2022021.
39. Wang, J.; Zhang, J. A real-space phase field model for the domain evolution of ferromagnetic materials. Int. J. Solids. Struct. 2013, 50, 3597-609.
40. Huang, Y. Y.; Jin, Y. M. Phase field modeling of magnetization processes in growth twinned Terfenol-D crystals. Appl. Phys. Lett. 2008, 93, 142504.
41. Shen, Z. H.; Wang, J. J.; Jiang, J. Y.; et al. Phase-field modeling and machine learning of electric-thermal-mechanical breakdown of polymer-based dielectrics. Nat. Commun. 2019, 10, 1843.
42. Bui, T. Q.; Hu, X. A review of phase-field models, fundamentals and their applications to composite laminates. Eng. Fract. Mech. 2021, 248, 107705.
43. Chen, L.; Zhao, Y. From classical thermodynamics to phase-field method. Prog. Mater. Sci. 2022, 124, 100868.
44. Wang, J.; Li, X. K.; Liu, C.; Shi, Y. N. Phase field simulations of microstructure evolution. Chin. J. Solid. Mechan. 2016, 37, 1-33.
45. Cahn, J. W. Free energy of a nonuniform system. II. Thermodynamic basis. J. Chem. Phys. 1959, 30, 1121-4.
46. Cahn, J. W.; Hilliard, J. E. Free energy of a nonuniform system. III. nucleation in a two-component incompressible fluid. J. Chem. Phys. 1959, 31, 688-99.
47. Cahn, J. W.; Allen, S. M. A microscopic theory for domain wall motion and its experimental verification in Fe-Al alloy domain growth kinetics. J. Phys. Colloques. 1977, 38, C7-51.
48. Allen, S. M.; Cahn, J. W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta. Metall. 1979, 27, 1085-95.
49. Clark, A. E.; Wun-Fogle, M. Modern magnetostrictive materials: classical and nonclassical alloys. Proc. SPIE. 2002, 4699, 421.
50. Deng, Z.; Dapino, M. J. Review of magnetostrictive vibration energy harvesters. Smart. Mater. Struct. 2017, 26, 103001.
51. Jiles, D. Recent advances and future directions in magnetic materials. Acta. Mater. 2003, 51, 5907-39.
52. Olabi, A.; Grunwald, A. Design and application of magnetostrictive materials. Mater. Des. 2008, 29, 469-83.
53. Klinger, T.; Pfutzner, H.; Schonhuber, P.; Hoffmann, K.; Bachl, N. Magnetostrictive amorphous sensor for biomedical monitoring. IEEE. Trans. Magn. 1992, 28, 2400-2.
54. Hart, S.; Bucio, R.; Dapino, M. Magnetostrictive actuation of a bone loading composite for accelerated tissue formation. Smart. Mater. Res. 2012, 2012, 1-7.
55. Clark, A. E. Chapter 7 Magnetostrictive rare earth-Fe2 compounds. Amsterdam: North-Holland Publishing Co.; 1980, pp. 531-89.
56. Zhang, J. X.; Chen, L. Q. Phase-field microelasticity theory and micromagnetic simulations of domain structures in giant magnetostrictive materials. Acta. Mater. 2005, 53, 2845-55.
57. Hubert, A.; Schafer, R. Magnetic domains: the analysis of magnetic microstructures. Berlin: Springe; 1998.
59. Hu, C. C.; Shi, Y. G.; Shi, D. N.; Tang, S. L.; Fan, J. Y.; Du, Y. W. Anisotropy compensation and magnetostrictive properties in
60. O’Handley, R. C. Modern magnetic materials: principles and applications. New York: Wiley; 1999. Available from: https://www.wiley.com/en-us/Modern+Magnetic+Materials%3A+Principles+and+Applications-p-9780471155669 [Last accessed on 25 Apr 2025]
61. Khachaturyan, A. G. Theory of structural transformation in solids. New York: Wiley; 2013. Available from: https://store.doverpublications.com/products/9780486783444?srsltid=AfmBOoqp5K0c7IvoyBkllCIrPmbaCngBtMhhWcV_MvzTq79RDwfwl65Y [Last accessed on 25 Apr 2025]
62. Artemev, A.; Jin, Y.; Khachaturyan, A. Three-dimensional phase field model of proper martensitic transformation. Acta. Mater. 2001, 49, 1165-77.
63. Wang, X.; Garcı́a-Cervera, C. J.; E, W. A gauss-seidel projection method for micromagnetics simulations. J. Comput. Phys. 2001, 171, 357-72.
64. Chen, L.; Shen, J. Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 1998, 108, 147-58.
65. Hu, C.; Zhang, Z.; Yang, T.; et al. Phase field simulation of grain size effects on the phase coexistence and magnetostrictive behavior near the ferromagnetic morphotropic phase boundary. Appl. Phys. Lett. 2019, 115, 162402.
66. Liu, J.; Jiang, C.; Xu, H. Giant magnetostrictive materials. Sci. China. Technol. Sci. 2012, 55, 1319-26.
67. Ren, W.; Zhang, Z. Progress in bulk MgCu2-type rare-earth iron magnetostrictive compounds. Chin. Phys. B. 2013, 22, 077507.
68. Atulasimha, J.; Flatau, A. B. A review of magnetostrictive iron-gallium alloys. Smart. Mater. Struct. 2011, 20, 043001.
69. Gou, J.; Ma, T.; Qiao, R.; Yang, T.; Liu, F.; Ren, X. Dynamic precipitation and the resultant magnetostriction enhancement in [001]-oriented Fe-Ga alloys. Acta. Mater. 2021, 206, 116631.
71. Yang, S.; Bao, H.; Zhou, C.; et al. Large magnetostriction from morphotropic phase boundary in ferromagnets. Phys. Rev. Lett. 2010, 104, 197201.
72. Bergstrom, R. J.; Wuttig, M.; Cullen, J.; et al. Morphotropic phase boundaries in ferromagnets: Tb1-xDyxFe2 alloys. Phys. Rev. Lett. 2013, 111, 017203.
73. Hunter, D.; Osborn, W.; Wang, K.; et al. Giant magnetostriction in annealed Co1-xFex thin-films. Nat. Commun. 2011, 2, 518.
74. Wang, B. L.; Jin, Y. M. Magnetization and magnetostriction of Terfenol-D near spin reorientation boundary. J. Appl. Phys. 2012, 111, 103908.
75. Zhou, C.; Ren, S.; Bao, H.; et al. Inverse effect of morphotropic phase boundary on the magnetostriction of ferromagnetic
76. Zhang, D.; Ma, X.; Yang, S.; Song, X. Role of the electronic structure in the morphotropic phase boundary of Tb1-xDyxCo2 studied by first-principle calculation. J. Alloys. Compd. 2016, 689, 1083-7.
77. Ma, T.; Liu, X.; Gou, J.; et al. Sign-changed-magnetostriction effect of morphotropic phase boundary in pseudobinary DyCo2-DyFe2 laves compounds. Phys. Rev. Mater. 2019, 3, 034411.
78. Hu, C.; Zhang, Z.; Cheng, X.; Huang, H.; Shi, Y.; Chen, L. Ultrasensitive magnetostrictive responses at the pre-transitional rhombohedral side of ferromagnetic morphotropic phase boundary. J. Mater. Sci. 2021, 56, 1713-29.
79. Wang, B.; Busbridge, S.; Li, Y.; Wu, G.; Piercy, A. Magnetostriction and magnetization process of Tb0.27Dy0.73Fe2 single crystal. J. Magn. Magn. Mater. 2000, 218, 198-202.
80. Zhao, Y.; Jiang, C.; Zhang, H.; Xu, H. Magnetostriction of <110> oriented crystals in the TbDyFe alloy. J. Alloys. Compd. 2003, 354, 263-8.
81. Jiles, D.; Thoelke, J. Theoretical modelling of the effects of anisotropy and stress on the magnetization and magnetostriction of
82. Desimone, A.; James, R. D. A theory of magnetostriction oriented towards applications. J. Appl. Phys. 1997, 81, 5706-8.
83. Zhao, X. G.; Lord, D. G. Effect of demagnetization fields on the magnetization processes in Terfenol-D. J. Magn. Magn. Mater. 1999, 195, 699-707.
84. Armstrong, W. D. An incremental theory of magneto-elastic hysteresis in pseudo-cubic ferro-magnetostrictive alloys. J. Magn. Magn. Mater. 2003, 263, 208-18.
85. Xu; YX; Cai, T. T.; Hu, C. C.; et al. Magnetic-field driven domain wall evolution in rhombohedral magnetostrictive single crystals: a phase-field simulation. Microstructures 2024, 4, 2024052.
86. Xu, Y.; Wu, Y.; Hu, C.; et al. Domain engineering in ferromagnetic morphotropic phase boundary with enhanced and non-hysteretic magnetostriction: a phase-field simulation. Scripta. Mater. 2024, 242, 115916.
87. Hu, C.; Yang, T.; Huang, H.; et al. Phase-field simulation of domain structures and magnetostrictive response in Tb1-xDyxFe2 alloys near morphotropic phase boundary. Appl. Phys. Lett. 2016, 108, 141908.
88. Ma, T.; Liu, X.; Pan, X.; et al. Local rhombohedral symmetry in Tb0.3Dy0.7Fe2 near the morphotropic phase boundary. Appl. Phys. Lett. 2014, 105, 192407.
89. Hu, C.; Zhang, Z.; Cai, T.; et al. Room-temperature ultrasensitive magnetoelastic responses near the magnetic-ordering tricritical region. J. Appl. Phys. 2021, 130, 063901.
90. Ke, X.; Zhou, C.; Tian, B.; et al. Direct evidence of magnetization rotation at the ferromagnetic morphotropic phase boundary in
91. Dai, M.; Demirel, M. F.; Liang, Y.; Hu, J. Graph neural networks for an accurate and interpretable prediction of the properties of polycrystalline materials. NPJ. Comput. Mater. 2021, 7, 574.
92. Sun, S.; Gong, Q.; Ni, Y.; Yi, M. A micromagnetic-mechanically coupled phase-field model for fracture and fatigue of magnetostrictive alloys. J. Mech. Phys. Solids. 2024, 191, 105767.
93. Rezaei, Y.; Jafari, M.; Jamshidian, M. Phase-field modeling of magnetic field-induced grain growth in polycrystalline metals. Comput. Mater. Sci. 2021, 200, 110786.
94. Guruswamy, S.; Srisukhumbowornchai, N.; Clark, A.; Restorff, J.; Wun-Fogle, M. Strong, ductile, and low-field-magnetostrictive alloys based on Fe-Ga. Scr. Mater. 2000, 43, 239-44.
95. Petculescu, G.; Wu, R.; Mcqueeney, R. Chapter three - Magnetoelasticity of bcc Fe-Ga Alloys. Elsevier; 2012, pp. 123-226.
96. Li, X.; Bao, X.; Yu, X.; Gao, X. Magnetostriction enhancement of Fe73Ga27 alloy by magnetic field annealing. Scr. Mater. 2018, 147, 64-8.
97. Gou, J.; Ma, T.; Liu, X.; et al. Large and sensitive magnetostriction in ferromagnetic composites with nanodispersive precipitates. NPG. Asia. Mater. 2021, 13, 276.
98. Yi, M.; Xu, B. X. A constraint-free phase field model for ferromagnetic domain evolution. Proc. R. Soc. A. 2014, 470, 20140517.
99. He, Y.; Ke, X.; Jiang, C.; et al. Interaction of trace rare-earth dopants and nanoheterogeneities induces giant magnetostriction in Fe-Ga alloys. Adv. Funct. Mater. 2018, 28, 1800858.
100. Yan, K.; Xu, Y.; Niu, J.; et al. Unraveling the origin of local chemical ordering in Fe-based solid-solutions. Acta. Mater. 2024, 264, 119583.
101. Zhang, J. X.; Chen, L. Q. Phase-field model for ferromagnetic shape-memory alloys. Philos. Mag. Lett. 2005, 85, 533-41.
102. Ullakko, K.; Huang, J. K.; Kantner, C.; O’handley, R. C.; Kokorin, V. V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett. 1996, 69, 1966-8.
103. Sozinov, A.; Likhachev, A. A.; Lanska, N.; Ullakko, K. Giant magnetic-field-induced strain in NiMnGa seven-layered martensitic phase. Appl. Phys. Lett. 2002, 80, 1746-8.
104. Lai, Y. W.; Scheerbaum, N.; Hinz, D.; et al. Absence of magnetic domain wall motion during magnetic field induced twin boundary motion in bulk magnetic shape memory alloys. Appl. Phys. Lett. 2007, 90, 192504.
105. Chen, H.; Wang, Y. D.; Nie, Z.; et al. Unprecedented non-hysteretic superelasticity of [001]-oriented NiCoFeGa single crystals. Nat. Mater. 2020, 19, 712-8.
106. Jin, Y. M. Effects of twin boundary mobility on domain microstructure evolution in magnetic shape memory alloys: Phase field simulation. Appl. Phys. Lett. 2009, 94, 062508.
107. Jin, Y. M. Domain microstructure evolution in magnetic shape memory alloys: phase-field model and simulation. Acta. Mater. 2009, 57, 2488-95.
108. Wu, P.; Ma, X.; Zhang, J.; Chen, L. Phase-field simulations of magnetic field-induced strain in Ni2MnGa ferromagnetic shape memory alloy. Philos. Mag. 2011, 91, 2102-16.
109. Peng, Q.; Huang, J.; Chen, M.; Sun, Q. Phase-field simulation of magnetic hysteresis and mechanically induced remanent magnetization rotation in Ni-Mn-Ga ferromagnetic shape memory alloy. Scr. Mater. 2017, 127, 49-53.
110. Peng, Q.; He, Y.; Moumni, Z. A phase-field model on the hysteretic magneto-mechanical behaviors of ferromagnetic shape memory alloy. Acta. Mater. 2015, 88, 13-24.
111. Sun, Y.; Luo, J.; Zhu, J. Phase field study of the microstructure evolution and thermomechanical properties of polycrystalline shape memory alloys: grain size effect and rate effect. Comput. Mater. Sci. 2018, 145, 252-62.
112. Wu, H. H.; Pramanick, A.; Ke, Y. B.; Wang, X. Real-space phase field investigation of evolving magnetic domains and twin structures in a ferromagnetic shape memory alloy. J. Appl. Phys. 2016, 120, 183904.
113. Xu, C.; Huang, Y.; Liang, Y.; Wu, P. Phase field simulations of microstructures in porous ferromagnetic shape memory alloy Ni2MnGa. Metals 2023, 13, 1572.
114. Xu, Y.; Hu, C.; Liu, L.; et al. A nano-embryonic mechanism for superelasticity, elastic softening, invar and elinvar effects in defected pre-transitional materials. Acta. Mater. 2019, 171, 240-52.
115. Rao, W.; Xu, Y.; Hu, C.; Khachaturyan, A. G. Magnetoelastic equilibrium and super-magnetostriction in highly defected pre-transitional materials. Acta. Mater. 2020, 188, 539-50.
116. Nan, C. W. Magnetoelectric effect in composites of piezoelectric and piezomagnetic phases. Phys. Rev. B. Condens. Matter. 1994, 50, 6082-8.
117. Srinivas, S.; Li, J. Y. The effective magnetoelectric coefficients of polycrystalline multiferroic composites. Acta. Mater. 2005, 53, 4135-42.
118. Ramesh, R.; Spaldin, N. A. Multiferroics: progress and prospects in thin films. Nat. Mater. 2007, 6, 21-9.
119. Ni, Y.; Khachaturyan, A. G. Phase field approach for strain-induced magnetoelectric effect in multiferroic composites. J. Appl. Phys. 2007, 102, 113506.
120. Zhang, J. X.; Li, Y. L.; Schlom, D. G.; et al. Phase-field model for epitaxial ferroelectric and magnetic nanocomposite thin films. Appl. Phys. Lett. 2007, 90, 052909.
121. Wu, P.; Ma, X.; Zhang, J.; Chen, L. Phase-field model of multiferroic composites: Domain structures of ferroelectric particles embedded in a ferromagnetic matrix. Philos. Mag. 2010, 90, 125-40.
122. Hu, J.; Sheng, G.; Zhang, J. X.; Nan, C. W.; Chen, L. Q. Phase-field simulation of strain-induced domain switching in magnetic thin films. Appl. Phys. Lett. 2011, 98, 112505.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data



























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].