Effect of material properties on the thermal responses of the carbonization and pyrolysis layers of polymer matrix composites for charring-ablators
Abstract
Ablative materials, a special type of thermal protection material, are widely used in extremely high-temperature environments such as hypersonic vehicles and re-entry capsules. They effectively mitigate heat conduction to the interior through ablation at the material surface. Based on traditional physical models and machine learning techniques, we systematically investigated the mapping relationship between multiple material parameters and thermal responses within the carbonized layer and pyrolysis layer of ablative materials. By employing high-throughput physical modeling and the sure independence screening and sparsity operator (SISSO) method for feature selection, we first revealed that the thermal responses of different layers are dominated by distinct material properties (e.g., density, thermal conductivity, heat capacity, etc.). The explicit relationships between the functioning material parameters and the features of the thermal response curves associated with single-/double-layer structures are well established. After the key parameter screening based on SISSO, we further developed a deep neural network surrogate model, capable of accurately predicting the entire thermal response process within the carbonized and pyrolysis layers.
Keywords
INTRODUCTION
During hypersonic re-entry, spacecraft such as returnable satellites and crew cabins encounter gas temperatures exceeding thousands of degrees Celsius. This extreme environment generates intense convective heat flux on vehicle surfaces, creating critical challenges for thermal protection systems. To address these challenges, advanced ablative materials[1,2] employ a dual-layer protection mechanism: a carbonized layer[3,4] and a pyrolysis layer[5]. The carbonized layer forms through high-temperature pyrolysis and acts as a primary thermal barrier. By absorbing and dissipating heat energy, it prevents structural components from reaching critical temperatures. Beneath this layer, the pyrolysis layer provides secondary insulation through endothermic reactions. These reactions actively absorb heat[6], significantly slowing thermal penetration. The synergy between these layers is crucial for maintaining structural integrity under extreme thermal conditions. Optimizing their properties enables the development of high-performance aerospace materials[7].
Accurately predicting thermal protection structures’ internal temperature fields is critical for the design of charring-ablators. However, experimental investigations face numerous challenges due to the extreme application scenarios. To overcome these challenges, computational modeling has become pivotal in evaluating charring-ablators’ performance. For example, Moyer et al. developed a finite difference-based aero thermal program for charring composites analysis[8]. Chen et al. established an implicit finite volume framework with moving grids for recession simulation[9-11]. In addition, the finite element ablation and thermal response[12,13] solver was developed to simulate one-, two-, or three-dimensional ablation, internal heat conduction, thermal decomposition, gas flow, and ablative material design in thermal protection systems. The factors concerning the thermal properties of chosen insulation materials can be various and will dominate the th ermal responses at different stages to different degrees during the service. These material parameters may include thermal conductivity (K)[14,15], heat capacity[12,13], permeability (k)[18,19], porosity (φ)[20,21], density (ρ)[22,23], etc., for both the raw material and the corresponding carbonized material. In addition, a considerable amount of uncertainty remains while obtaining these parameters through experimental measurement[24-26]. As a result, the combined effect of these parameters and, therefore, the underlying working mechanism on the thermal responses of both the carbonization and pyrolysis layers are complex.
In terms of computational modeling and simulations, existing work on multilayer resin-based composite materials faces several notable challenges and limitations. For example, the finite element method (FEM) is limited to solving heat transfer problems in systems with fewer parameters[27-29]. For systems with a larger number of parameters, the modeling complexity increases rapidly, leading to a significant decrease in computational efficiency[30,31]. Moreover, while the FEM is capable of achieving forward prediction of material thermal response, it cannot rapidly and accurately assess the primary and secondary parameters that influence this thermal response performance[32-34]. Such physics-based models are developed based on complex theories and equations, which raises the technical threshold and may bring about certain difficulties for those with less professional backgrounds. The surrogate model therefore needs to be built to replace the physics-based models with complicated equations by bridging the material parameters and performance simply through explicit/implicit data analysis, thus improving the computing efficiency.
From the perspective of the Materials Genome Initiative[35], exploring the relationship between material structures and properties through large-scale computational simulations, data mining, and experimental validation is an efficient way to predict and optimize material characteristics, and thus accelerate the discovery and design of new materials for future innovations. With the help of databases facing divergent scopes, data-driven accelerated materials research[36] is an emerging approach within the scope of the Materials Genome Initiative, allowing researchers to expedite material development processes. Jha et al. utilized the robust capabilities and elegance of deep learning to directly extract material properties from the elemental composition of materials, effectively overcoming the constraints imposed by contemporary machine learning techniques reliant on manual feature engineering[37]. Chen et al. utilized the finite-volume direct averaging micromechanics to simulate the uniaxial and cyclic responses of unidirectional composite materials at various off-axis angles, which were used as inputs to train a two-layered long short-term memory (LSTM) neural network (NN), establishing the mapping between applied strains and corresponding stresses, yielding promising results in subsequent testing[38]. In addition, Sun et al. employed a data-driven approach to explore the chemical phase space of ternary nitrides, and expanded the known 307 combinations within the chemical phase space associated with the nitrides to 6,000 hypothetical structures[39]. Further first-principles calculations reveal 244 novel nitrides, with 93 having never been reported before. Some examples[40-45] involving data-driven approaches have also been reported, aiming at predicting material properties by advanced machine learning techniques.
In line with the principles of data-driven materials research, this study focuses on the direct relationship between various material properties and the thermal responses of carbonization and pyrolysis layers. To develop an NN-based surrogate model for predicting this relationship, we first calculate the accurate temperature fields associated with the material parameters using FEM. This is followed by a parameter screening process utilizing sure independence screening and sparsity operator (SISSO)[46,47] regression. This screening process effectively eliminates material parameters that have minimal impact on the macroscopic performance of the multilayer composites, thereby reducing the dimensionality of the surrogate model input. Through these surrogate models, we establish both explicit and implicit relationships between various material properties and their thermal performance during ablation. Specifically, the explicit relationship derived from SISSO enables inverse parameter design for optimizing thermal performance, while the implicit relationships developed using the NN facilitate rapid predictions of the thermal response curve across the entire time range for known material parameters. The rest of the paper is organized as follows. Section “MATERIALS AND METHODS” outlines the heat conduction model, the SISSO regression model, and the deep NN model. Details on data proliferation and model parameters are described in Section “Thermal responses of the first layer and the double layer”. The main results are shown and discussed in Section “Assessment of the effect of functioning parameters” and Section “Error analysis of the SISSO model”. Major conclusions are summarized in Section “CONCLUSIONS”.
MATERIALS AND METHODS
Physics-based model and equations
The ablation process of carbonaceous materials can be described by the typical layered model[48] [Figure 1]. The first layer of the material nearest to the heat source is called the carbonized layer, which is a porous material formed by complete pyrolysis of the original material. Between the carbonized layer and the original material layer is the second layer, where pyrolysis reactions are taking place. The pyrolysis reactions absorb heat, and the resulting pyrolysis gases flow within the carbonized layer, thereby hindering heat transfer. Therefore, the carbonized layer and the pyrolysis layer are of great importance as they work as the blocking medium that absorbs and thus stops the heat flux from transferring to the original material. In this work, we focus on the one-dimensional thermal responses along the black arrow direction and (1) at the inner side of the carbonized layer, (2) at the inner side of the pyrolysis layer, as respectively shown by the red and blue arrows in Figure 1A. Note that the carbonized layer and the pyrolysis layer in this work are referred to as the “first layer” and the “second layer” for convenience.
Figure 1. (A) The one-dimensional simulation unit in this work, abstracted from the layered model schematically shown in (B). While the thermal response of the single layer is represented by the temperature variation at the inner side of the first layer [indicated by the red arrow in (A)], the thermal response of the double-layer structure is represented by the temperature at the inner side of the second layer [indicated by the blue arrow in (A)].
Based on the simulation unit described above, energy conservation[48], i.e., the evolution of temperature, can be established in a moving coordinate system:
where K is the thermal conductivity, ρ is the material density, hg is the enthalpy of pyrolysis gas, vg and vm are the viscosities of the pyrolysis gas and the control volume, respectively, and cp is the specific heat capacity of the solid material. With these material properties, the term
SISSO symbolic regression
SISSO[54] is a powerful machine learning approach combining conformal regression and compressed sensing to derive explicit mathematical expressions. It begins by generating a wide array of possible expressions based on user-defined input variables and mathematical operators, forming an extensive expression space fi. The machine learning objective is then expanded offline as P = ∑βifi with the optimal sparse solution obtained using sure independence screening (SIS) and sparse operator (SO). Given the model’s typically low dimensionality (fewer than five non-zero coefficients), SISSO is versatile for both large and small datasets, selecting key variables and optimizing their interactions. While lacking direct physical interpretability, it effectively identifies influential factors (“material genes”) in the properties of the target material.
Deep-learning NN
Deep learning[55,56], characterized by its multilayer architecture of neurons, excels in modeling complex relationships in high-dimensional datasets by leveraging nonlinear transformations via activation functions. This hierarchical feature extraction allows the network to progressively learn abstract representations of input data. Key components of deep learning include perceptrons[57], activation functions[58] [e.g., rectified linear unit (ReLU), sigmoid], optimizers, and loss functions[59] [e.g., mean squared error (MSE), binary cross-entropy (BCE)]. These elements work together to iteratively adjust weights through algorithms such as stochastic gradient descent, improving accuracy by minimizing loss. A major advantage of deep learning is its ability to reduce dependence on extensive feature engineering, which is often required in traditional machine learning. In fields such as science and engineering, deep learning autonomously extracts relevant features, uncovering non-intuitive patterns through a data-driven approach[60]. It performs especially well with large datasets, increasing accuracy with more data, and remains efficient at making rapid predictions after the initial computational cost of training.
To provide a clearer understanding of the overall framework and logical relationships of the methods employed in this study, a research workflow diagram is presented in Figure 2. This flowchart seamlessly integrates the physics-based model, the symbolic regression method (SISSO), and deep learning NN applications. It comprehensively outlines the research pathway, starting from physical parameter modeling and culminating in performance prediction. By combining theoretical guidance from the physics-based model with the flexibility and efficiency of data-driven methods, this integrated approach offers a robust solution for predicting the thermal response of complex multilayer materials. The workflow starts with a physics-based model that uses the energy conservation equation to derive key thermophysical parameters, such as the specific heat capacity at constant pressure (cp), K, ρ, k and φ which form the basis for further analysis. The SISSO method then carefully weighs the roles of all material parameters at different stages during material ablation, to screen out the functioning parameters that determine the thermal response. Finally, these parameters are input into deep-learning NNs to predict temperature fields and performance trends under diverse thermal conditions, achieving high-precision thermal response predictions for multilayer materials.
Figure 2. Illustration of the intrinsic connections among the three key steps of the current work: the physics-based model supports the input data, the SISSO method optimizes the data, and the deep learning model completes the final prediction task. SISSO: Sure independence screening and sparsity operator.
RESULTS AND DISCUSSION
Thermal responses of the first layer and the double layer
The physics-based thermal response model in this work is developed by FEM based on multiphysics object oriented simulation environment (MOOSE)[61]. Due to the carbonization caused during the ablation, the heat transfer process is in general affected by both the raw material consisting of the component and the part that is already carbonized. The first and second layers of the material collectively form a defense line for ablation protection, determining the working state of the composite material. Our previous work[48] has shown that five pairs of raw/carbonized material parameters, i.e., the specific heat capacity at cp, K, ρ, k, and φ, play an important role in the thermal conduction process through the first and second layers. To distinguish the difference of these pairs of parameters, it should be emphasized again that parameters with footnote v are for raw materials, and those with c for carbonized materials. The parameters of the above two layers are shown in Tables 1 and 2.
Parameters for the material of the first layer(carbonized layer) used in the thermal response model and machine learning model in the present work[62]
| Parameters | Density | Heat capacity | Thermal conductivity | Porosity | Permeability |
| ρv/ρc* | cp,v/cp,c | Kv/Kc | φv/φc | kv/kc | |
| Unit | kg/m3 | J/(kg)/K | W/(m·K) | - | m2 |
| Average values | 880/642 | 544/811 | 0.1269/0.1265 | 0.8/0.85 | 1.6/2.0 × 10-11 |
| Deviation | ±6% | ±5%/±10% | ±10%/±20% | ±8% | ±10% |
Parameters for the material of the second layer(pyrolysis layer) used in the thermal response model and machine learning model in the present work[62]
| Parameters | Density | Heat capacity | Thermal conductivity | Porosity | Permeability |
| ρv/ρc* | cp,v/cp,c | Kv/Kc | φv/φc | kv/kc | |
| Unit | kg/m3 | J/(kg)/K | W/(m·K) | - | m2 |
| Average values | 495.4/214 | 653/711 | 0.04824/0.1365 | 0.8/0.85 | 1.6/2.0 × 10-11 |
| Deviation | ±6% | ±5%/±10% | ±10%/±20% | ±8% | ±10% |
The temperature evolution in the multilayer material during ablation is depicted in Figure 3, illustrating distinct thermal behaviors in each layer. First, we focus on the thermal response of the inner surface of the first layer (i.e., the position indicated by the red arrow in Figure 1A). Using the material parameters listed in Table 1, the temperature distributions from the surface to the inner part of the first layer at time steps t = 0, 2, 4, 6, and 1,000 dimensionless time are shown in Figure 3A. The corresponding temperature variation at the inner surface over time is presented in Figure 3C, where the temperature rapidly rises and stabilizes around 900 K after approximately 200 s, indicating efficient heat transfer and rapid thermal equilibrium. The thermal response from the surface to the interior of the pyrolysis layer is shown in Figure 3B. It should be noted that the thermal response associated with the double layers is determined by the material parameters of both the first and the second layers, listed in Tables 1 and 2. Compared with that of the single carbonized layer, the thermal response of the double layers (consisting of the carbonization and the pyrolysis layers) exhibits quite different behaviors. For example, the temperature at the inner side of the pyrolysis layer, also defined as the back temperature, remains unchanged at the initial stage as the heart flux has not arrived yet, as depicted in Figure 3D. At a later stage after t = 50, the temperature rises gradually and reaches around
Figure 3. (A) The temperature changes in the single-layer structure during the ablation process by FEM; (B) The temperature changes in the inner side of the double-layer structure by FEM; (C) The temperature variations of T1 at the inner side of the first layer [red arrow in (A)]; (D) The temperature variations T2 at the inner side of the second layer [blue arrow in (B)]. Note that the temperature curve in (D) is also known as the back temperature curve. FEM: Finite element method.
It has been proved by previous work[62] that for a given material system, the above parameters will vary over a certain range of about 6%-20% due to mechanical processing, which will alter the thermal responses during ablation heat conduction. To systematically investigate parameter sensitivity, we conducted a computational parametric analysis employing high-fidelity FEM coupled with high-throughput computational simulations. The experimental design proceeded as follows:
A. Single-layer parameter characterization
Material parameters of the second layer were maintained at nominal values [Table 2] while systematically modulating the first layer parameters within predefined ranges [Table 1]. 1,408 distinct computational experiments are conducted for parametric study, each producing time-dependent thermal evolution profiles through fully coupled thermomechanical FEM simulations.
B. Multilayer interaction analysis
A combinatorial parameter space investigation was implemented by concurrently varying material properties of both layers [Tables 1 and 2]. This protocol yielded 1,344 additional simulation cases, facilitating the quantification of cross-layer parameter coupling effects.
All input parameter combinations and corresponding thermal response data were algorithmically cataloged using a relational database architecture, ensuring strict bijective mapping between input vectors (n-dimensional) and output thermal signatures.
Assessment of the effect of functioning parameters
In our preliminary research, we evaluated two prominent methods for handling high-dimensional data, particularly in the context of complex systems in materials science: SISSO and least absolute shrinkage and selection operator (LASSO)[63-65]. Through a rigorous comparative analysis, we determined that SISSO offers superior performance over LASSO in terms of model simplicity and physical interpretability. As a result, we selected SISSO as the primary algorithmic framework for this study. Specifically, the systematic application of the SISSO algorithm reveals statistically significant advantages over traditional LASSO regression, as detailed in the Supplementary Materials. While both methods demonstrate high predictive accuracy, SISSO produces more parsimonious models requiring fewer critical parameters. Crucially, the purely linear models generated by LASSO are insufficient for capturing the nonlinear interactions inherent in complex material systems, whereas SISSO excels in representing these nonlinear relationships[54,66-68]. These combined advantages of model simplicity, nonlinear representational capacity, and physical interpretability motivated our decision to adopt SISSO.
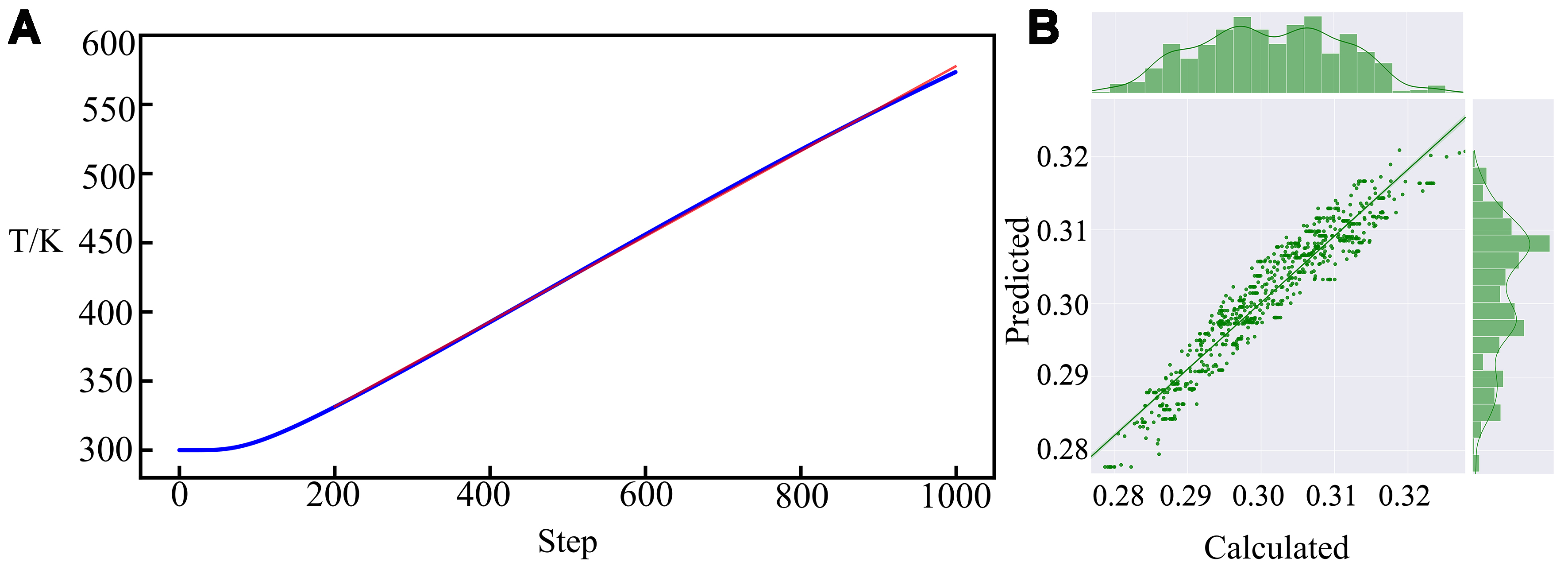
Starting with the thermal response of the first layer, we divide the temperature profile depicted in Figure 4A into two main phases: the rapid temperature rise stage and the plateau stage. It is apparent that the rapid temperature rise phase witnesses the increase in temperature from 300 to ~700 K within 50 time steps and is therefore crucial in determining the final inner side temperature of the first layer. To explore the factors affecting temperature increase during this phase, we introduced a fitting parameter Kstart_1 (subscript “1” represents the first layer), which characterizes the slope of the curve during the rapid heating stage, as indicated by the red line in Figure 4A. Using Kstart_1 as the fitting target, we employed symbolic regression via the SISSO algorithm to derive an analytical solution, expressed as a function of all the material properties listed in Table 1, as given in
Figure 4. (A) Schematic diagram of the slope fitting during the rapid temperature rise phase of the first layer material; the blue scatter plot represents the original temperature curve, the red line represents the fitted slope, the star mark represents the final temperature; (B) Regression analysis graph for Kstart_1 (the bar charts above and to the right represent the data distribution).
which reveals that this rapid heating-up stage is primarily correlated with the density ρv_1, thermal conductivity Kv_1, and heat capacity cp,v_1 of the first layer. Its root mean squared error (RMSE), a measure of the average difference between predicted and actual values, is 0.0252, and Figure 4B shows the regression analysis plot of the obtained model.
Besides, as can be seen in Figure 1A, the inner side temperature of the first layer acts as the initial temperature at the outer surface of the pyrolysis layer. Therefore, to reduce the heat conduction rate in the whole double-layer structure, it is necessary to control the inner side temperature of the first layer. Based on this point, we analyzed the effects of material parameters of the first layer on the endpoint temperature in Figure 4A with a star mark through the SISSO regression. The result is given in
with RMSE being 0.08, which suggests that the endpoint temperature exhibits a significant dependence on the thermal conductivity Kv_1/Kc_1 of the first layer of material before and after carbonization.
Similarly, we also assessed the effect of material parameters of both the two layers [Tables 1 and 2] on the temperature rise stage (see the red line in Figure 5A) of the back temperature evolution profile. The relationship between the slope at this stage, Kend_2 (subscript “2” represents the second layer, the pyrolysis layer), and the material properties can be expressed explicitly as
Figure 5. (A) Schematic diagram of the fitted slope at the end of temperature rise of the second layer; the red line represents the fitted straight line, the blue scatter line represents the original temperature curve; (B) Regression analysis graph for Kend_2 (the bar charts above and to the right represent the data distribution).
with RMSE being 0.003, and Figure 5B shows the regression analysis plot of the obtained model.
Kend_2 is a function of the densities of the second layer’s raw material ρv_2, the K of the second layer’s material Kv_2 and that of the second layer’s carbonized material Kc_2, and the first layer’s carbonized material Kc_1.
Error analysis of the SISSO model
Error analysis for the Kstart_1 model, derived from SISSO regression, was conducted on both the training set (1,126 groups, Figure 6A) and the testing set (282 groups, Figure 6B). The residuals demonstrate highly consistent predictive accuracy and robustness within the data coverage range (predicted values: 18.4-19.6). For the training set, the residuals exhibit a mean of 4.03 × 10-5 and a standard deviation (σ) of 0.0252, with 95% of residuals concentrated within ± 0.05 (actually observed range: -0.06 to +0.06). The testing set residuals exhibit a mean of -1.61 × 10-4 and σ = 0.0262, with 95% distributed within ± 0.06. Both datasets closely approximate a normal distribution [density curves N(μ,σ) suit well], and the relative error rate is only 0.13% (based on the median predicted value of 19.0), confirming the absence of systematic bias and minimal error fluctuation. In the residual vs. predicted value scatter plots, the LOWESS trend line[69] slopes for the training and testing sets are 0.002 and 0.001, respectively, with residuals equally distributed around the zero line (range: -0.08 to +0.06). This indicates stable error variance (homoscedasticity) and no systematic overestimation or underestimation. In summary, the model demonstrates no significant systematic bias within the data coverage range, with well-controlled error fluctuations.
Figure 6. Error analysis of SISSO models. (A and B) Residual distributions (left) and residual-predicted value plots (right) for the Kstart_1 model. Training set (1,126 samples): Residuals follow a normal distribution (μ = 4.03 × 10-5, σ = 0.0252), with 95% within ± 0.05. LOWESS trend line slope = 0.002; Testing set (282 samples): Residuals (μ = -1.61 × 10-4, σ = 0.0262) show 95% within ± 0.06. LOWESS slope = 0.001; (C and D) Error analysis for the Kend_2 model. Training set (1,075 samples): Residuals (μ = 1.19 × 10-4, σ = 3.02 × 10-3) are 95% within ± 6 × 10-3. LOWESS slope = 0.009. Testing set (269 samples): Residuals (μ = 9.40 × 10-5, σ = 2.79 × 10-3) show 95% within ± 6 × 10-3. LOWESS slope = 0.002. SISSO: Sure independence screening and sparsity operator; LOWESS: locally weighted scatterplot smoothing.
Error analysis for the Kend_2 model, based on the training set (1,075 groups, Figure 6C) and testing set (269 groups, Figure 6D), reveals high precision and stability across both datasets. The training set residuals approximate a normal distribution (mean μ = 1.19 × 10-4, σ = 3.02 × 10-3), with 95% of residuals concentrated within ± 6 × 10-3 (observed range: -6 × 10-3 to +8 × 10-3). The testing set residuals similarly follow normality
To quantify robustness against data variability, 500 bootstrap iterations were conducted. Figure 7 displays the distributions of RMSE (blue), MAE (orange), and R2 (green) calculated from 500 resampled iterations. Figure 7A: RMSE: Centered at 2.8 × 10-3 [95% confidence interval (CI): 2.4-2.8 × 10-3], MAE: Spread between 1.97-2.30 × 10-3 (peak frequency at 60). R2: Moderately high performance (95%CI: 0.986-0.990), explaining > 90% variance. Figure 7B: RMSE: Tightly distributed around 0.003 (95%CI[70]: 2.8-3.2 × 10-3), reflecting minimal prediction deviation. MAE: Narrow range (95%CI: 2.4-2.75 × 10-3) with peak frequency at 80. R2: Values cluster near 0.90 (95%CI: 0.873-0.911), indicating near-perfect explanatory power.
Prediction of whole time-series thermal responses by deep NN
To expedite the data acquisition and property prediction process, we intend to utilize a surrogate model as a substitute for the full FEM simulation to capture the feature of the evolving back temperature during material ablation with known material parameters of the carbonized layer and the pyrolysis layer. This allows us to gain insights into the optimization and design of thermal insulation materials. Consequently, we have developed a NN model using the available data. Based on the above SISSO regression analysis, we developed a NN and extracted seven functioning parameters (i.e., Kc_1, Kc_2, Kv_2, Kv_1, cp,v_1, ρv_2, ρv_1) out of the original 20 parameters (listed in Tables 1 and 2) to serve as the input of the network. In this study, we employed deep learning to analyze the temperature profiles of ablation resistance in multilayer materials, considering two distinct input configurations: using only the parameters of the first layer and combining the parameters of both layers. Figure 8A illustrates the loss curve over 1,000 epochs, where only the parameters of the first layer were used to model the thermal response of that layer. The steady decrease in training loss indicates the convergence of the model. Figure 8B presents the comparison between predicted and observed thermal responses after training; the blue circles represent observed (true) values, while the red line denotes the model’s predictions. The close alignment between the predicted and observed values demonstrates high predictive accuracy. Likewise, Figure 8C shows the loss curve over 1,000 epochs when the parameters of both the first and second layers were included in the model. The observed convergence pattern suggests that the model effectively learned the combined parameter set. Figure 8D compares the predicted and observed thermal responses for this model, once again showing strong agreement between the predicted red curve and the observed blue circles, further affirming the model’s accuracy in capturing the thermal response of multilayer composites. Utilizing a pre-trained surrogate model enables the rapid generation of a large dataset of back-temperature profiles, facilitating efficient exploration of thermal behavior in multilayer materials.
Figure 8. (A) The loss curve of 1,000 epochs of deep learning training using only the first layer parameters; (B) The comparison between the data obtained by FEM (blue circles) and prediction of the deep learning model (red line) for the single layer structure (i.e., the first layer); (C) The loss curve of 1,000 epochs of deep learning training using only two layers of parameters; (D) The comparison between the data obtained by FEM (blue circles) and the prediction of the deep learning model (red line) for the double-layer structure (i.e., the first layer and the second layer). FEM: Finite element method.
CONCLUSIONS
The thermal responses, described by the temperature evolution curves under fixed boundary conditions, are simulated using a finite element model incorporated in MOOSE. High-throughput calculations are then carried out to derive different temperature evolution curves with varying material parameters. The relationships between thermal responses and material properties are meticulously investigated and analyzed by SISSO regression and NNs. The primary findings include:
(1) In our study, the thermal response of both carbonization and pyrolysis layers is significantly influenced by seven key parameters (i.e., Kc_1, Kc_2, Kv_2, Kv_1, cp,v_1, ρv_2, ρv_1). These properties govern the heat transfer processes and determine the ablation protection effectiveness of the material.
(2) Regression analysis through SISSO reveals the key functioning parameters that determine the thermal responses of carbonization and pyrolysis layers. The rapid temperature rise in the first layer is mainly affected by the first-layer material’s density ρv_1, thermal conductivity Kv_1, and heat capacity cp,v_1. The heating rate of the second layer depends on three key parameters: the K of the second-layer raw material
(3) Deep learning NNs are further established to correlate the functioning parameters of materials to the thermal response curves concerning the single first layer (carbonized layer) and double layers (carbonization and pyrolysis layers), respectively. This pre-trained surrogate model enables the rapid generation of extensive back-temperature data, facilitating efficient exploration of thermal behavior in multilayer materials.
DECLARATIONS
Authors’ contributions
Proposed and conceptualized the theme and framework of this article; collected and analyzed the literature; and wrote the manuscript: Li, Y.
Provided the finite element model: Liu, X.
Supervised and revised the manuscript: Qiu, D; Yang, J; Xie, W.
Recommendations for methods and ideas: Wang, X.
Availability of data and materials
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Financial support and sponsorship
This work is supported by the National Key Research and Development Program of China under Grant No. 2022YFB3707803 and the National Natural Science Foundation of China under Grant No. U2230102. JY acknowledges the support from the Shanghai Engineering Research Center for Integrated Circuits and Advanced Display Materials.
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
Supplementary Materials
REFERENCES
1. Soni, R.; Verma, R.; Kumar, G. R.; Singh, H. Progress in aerospace materials and ablation resistant coatings: a focused review. Opt. Laser. Technol. 2024, 177, 111160.
2. Guo, M.; Yu, K.; Yang, J.; Zhang, P.; Zhang, Y.; Zhu, D. B2O3-reinforced ablative materials with superior and comprehensive ablation resistance used in aerospace propulsion thermal protection systems. Polym. Degrad. Stab. 2024, 223, 110740.
3. Kumar, A.; Ranjan, C.; Kumar, K.; Reddy, M. H.; Babu, B. S.; Katiyar, J. K. State-of-the-art on advancements in carbon-phenolic and carbon-elastomeric ablatives. Polymers 2024, 16, 1461.
4. Xu, W.; Song, W.; Jia, X.; et al. Nano-silica modified lightweight and high-toughness carbon fiber/phenolic ablator with excellent thermal insulation and ablation performance. Def. Technol. 2024, 31, 192-9.
5. Xia, C.; Xie, W.; Meng, S.; Gao, B.; Ye, J. Preparation of integrated carbon fiber stitched fabric reinforced (SiBCN) ceramic/resin double-layered composites for ablation resistance, thermal insulation and compression resistance performance. Compos. Sci. Technol. 2024, 252, 110629.
6. Vekariya, N.; Patel, B.; Patel, R.; Valand, J. Microstructural investigation and performance of carbon matrix composites developed through facile pitch modification route. Diam. Relat. Mater. 2024, 145, 111056.
7. Agarwal, N.; Rangamani, A.; Bhavsar, K.; et al. An overview of carbon-carbon composite materials and their applications. Front. Mater. 2024, 11, 1374034.
8. Moyer, C. B.; Wool, M. R. Aerotherm charring material thermal response and ablation program, version 3. volume 1. Program description and sample problems. 1970. https://archive.org/details/DTIC_AD0875062. (accessed 11 Apr 2025)
9. Chen, Y. K.; Milos, F. Three-dimensional ablation and thermal response simulation system. In Proceedings of the 38th AIAA thermophysics conference, Toronto, Canada. Jun 06-09, 2005. 2012; pp. 5064.
10. Chen, Y. K.; Milos, F. Multidimensional effects on heatshield thermal response for the Orion crew module. In Proceedings of the 39th AIAA Thermophysics Conference, Miami, USA. Jun 25-28, 2007. 2012; pp. 4397.
11. Chen, Y. K.; Milos, F.; Gokcen, T. Validation of a three-dimensional ablation and thermal response simulation code. In Proceedings of the 10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, Chicago, USA. Jun 28 - Jul 01, 2010. 2012; pp. 4645.
12. Dec, J. A. Three dimensional finite element ablative thermal response analysis applied to heatshield penetration design. 2010. https://www.proquest.com/openview/6f7df22a64ad48ff6a7b07b10532fcb4/1?cbl=18750&pq-origsite=gscholar. (accessed 11 Apr 2025).
13. Dec, J.; Laub, B.; Braun, R. Two-dimensional finite element ablative thermal response analysis of arcjet stagnation tests. In Proceedings of the 42nd AIAA Thermophysics Conference, Honolulu, USA. Jun 27-30, 2011. 2012; pp. 3617.
14. Kavimani, V.; Gopal, P. M.; Thankachan, T.; Sivamaran, V. 5 - Evolution and recent advancements of composite materials in thermal applications. In: Applications of Composite Materials in Engineering. Elsevier; 2025. pp. 119-38.
15. Meicong, W.; Xin, Y.; Jixiang, S.; et al. Effect of phenolic resin pyrolysis on thermal properties of SiFRP composites under high heating rates. J. Phys. Conf. Ser. 2024, 2891, 112023.
16. Song, J.; Zhang, Y. Effect of an interface layer on thermal conductivity of polymer composites studied by the design of double-layered and triple-layered composites. Int. J. Heat. Mass. Transfer. 2019, 141, 1049-55.
17. Xu, Y.; Ye, H.; Zhang, L.; Cai, Q. Investigation on the effective thermal conductivity of carbonized high silica/phenolic ablative material. Int. J. Heat. Mass. Transfer. 2017, 115, 597-603.
18. Alotaibi, H. Numerical modelling of manufacturing of graphene-modified hybrid composites for structural applications. 2023. https://www.proquest.com/openview/20298841422af4144c4020fb69aa34df/1?cbl=2026366&diss=y&pq-origsite=gscholar. (accessed 11 Apr 2025).
19. Kumar, C. V.; Kandasubramanian, B. Advances in ablative composites of carbon based materials: a review. Ind. Eng. Chem. Res. 2019, 58, 22663-701.
20. Guo, N.; Wang, M.; Wang, J.; Wu, Z.; Gao, J. Utilizing a multi-layer structure to regulate the thermal conductivity of an advanced BN + EP composite insulation material: effects of content, number of layers, and curing temperature on composites. Polym. Compos. 2024, 45, 3536-50.
22. Reis, L. M. M.; da Silveira, P. H. P. M.; Chaves, Y. S.; et al. Thermal and ballistic characterization of epoxy matrix composites reinforced with babassu (Attalea speciosa) fiber: an experimental investigation. J. Mater. Res. Technol. 2025, 35, 2176-87.
23. Chen, L.; Zhao, P.; Xie, H.; Yu, W. Thermal properties of epoxy resin based thermal interfacial materials by filling Ag nanoparticle-decorated graphene nanosheets. Compos. Sci. Technol. 2016, 125, 17-21.
24. Guo, L.; Peng, J.; Guo, C.; Huo, C.; Sun, R.; Zhang, Y. Ablation performance of supersonic atmosphere plasma sprayed tungsten coating under oxyacetylene torch and plasma torch. Vacuum 2017, 143, 262-70.
25. Zha, B. L.; Su, Q. D.; Shi, Y. A.; Wang, J. J.; He, Q. Study on plasma ablation behavior of C/C composite materials under particle erosion. IOP. Conf. Ser. Mater. Sci. Eng. 2018, 423, 012094.
26. Yi, Z.; Ran, L.; Yi, M. Differences in microstructure and properties of C/C composites brazed with Ag-Cu-Ti and Ni-Cr-P-Ti pasty brazing filler. Vacuum 2019, 168, 108804.
27. Yuan, W.; Yu, N.; Li, L.; Fang, Y. Heat transfer analysis in multi-layered materials with interfacial thermal resistance. Compos. Struct. 2022, 293, 115728.
28. Huang, H. C.; Usmani, A. S. Introduction. In: Finite element analysis for heat transfer. London: Springer; 1994. p. 1-5.
29. Bergheau, J. M.; Fortunier, R. Finite element simulation of heat transfer. John Wiley & Sons: 2013.
30. Hu, M.; Yang, Z. Perspective on multi-scale simulation of thermal transport in solids and interfaces. Phys. Chem. Chem. Phys. 2021, 23, 1785-801.
31. Ma, T.; Chakraborty, P.; Guo, X.; Cao, L.; Wang, Y. First-principles modeling of thermal transport in materials: achievements, opportunities, and challenges. Int. J. Thermophys. 2020, 41, 2583.
32. Łach, Ł.; Svyetlichnyy, D. Advances in numerical modeling for heat transfer and thermal management: a review of computational approaches and environmental impacts. Energies 2025, 18, 1302.
33. Yao, H.; Gao, Y.; Liu, Y. FEA-Net: A physics-guided data-driven model for efficient mechanical response prediction. Comput. Methods. Appl. Mech. Eng. 2020, 363, 112892.
34. Zhu, C.; Bamidele, E. A.; Shen, X.; Zhu, G.; Li, B. Machine learning aided design and optimization of thermal metamaterials. Chem. Rev. 2024, 124, 4258-331.
35. de Pablo, J. J.; Jackson, N. E.; Webb, M. A.; et al. New frontiers for the materials genome initiative. npj. Comput. Mater. 2019, 5, 173.
36. Pollice, R.; Dos Passos Gomes, G.; Aldeghi, M.; et al. Data-driven strategies for accelerated materials design. Acc. Chem. Res. 2021, 54, 849-60.
37. Jha, D.; Ward, L.; Paul, A.; et al. ElemNet: deep learning the chemistry of materials from only elemental composition. Sci. Rep. 2018, 8, 17593.
38. Chen, Q.; Jia, R.; Pang, S. Deep long short-term memory neural network for accelerated elastoplastic analysis of heterogeneous materials: an integrated data-driven surrogate approach. Compos. Struct. 2021, 264, 113688.
39. Sun, W.; Bartel, C. J.; Arca, E.; et al. A map of the inorganic ternary metal nitrides. Nat. Mater. 2019, 18, 732-9.
40. Liu, B.; Wang, D.; Avdeev, M.; Shi, S.; Yang, J.; Zhang, W. High-throughput computational screening of Li-containing fluorides for battery cathode coatings. ACS. Sustainable. Chem. Eng. 2020, 8, 948-57.
41. Hautier, G.; Jain, A.; Chen, H.; Moore, C.; Ong, S. P.; Ceder, G. Novel mixed polyanions lithium-ion battery cathode materials predicted by high-throughput ab initio computations. J. Mater. Chem. 2011, 21, 17147.
42. Mounet, N.; Gibertini, M.; Schwaller, P.; et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotechnol. 2018, 13, 246-52.
43. Huang, W.; Martin, P.; Zhuang, H. L. Machine-learning phase prediction of high-entropy alloys. Acta. Mater. 2019, 169, 225-36.
44. Islam, N.; Huang, W.; Zhuang, H. L. Machine learning for phase selection in multi-principal element alloys. Comput. Mater. Sci. 2018, 150, 230-5.
45. Shin, S.; Ko, B.; So, H. Noncontact thermal mapping method based on local temperature data using deep neural network regression. Int. J. Heat. Mass. Transfer. 2022, 183, 122236.
46. Ouyang, R.; Curtarolo, S.; Ahmetcik, E.; Scheffler, M.; Ghiringhelli, L. M. SISSO: a compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates. Phys. Rev. Mater. 2018, 2, 083802.
47. Bartel, C. J.; Sutton, C.; Goldsmith, B. R.; et al. New tolerance factor to predict the stability of perovskite oxides and halides. Sci. Adv. 2019, 5, eaav0693.
48. Liu, X.; Guo, Y.; Liu, W.; Zeng, L. Numerical simulation research on three dimensional ablative thermal response of charring ablators. J. Astronaut. 2016, 37, 1150-6. (in Chinese).
49. Dewey, W. C. Arrhenius relationships from the molecule and cell to the clinic. Int. J. Hyperthermia. 1994, 10, 457-83.
50. Peleg, M.; Normand, M. D.; Corradini, M. G. The Arrhenius equation revisited. Crit. Rev. Food. Sci. Nutr. 2012, 52, 830-51.
51. Appleton, J. P.; Bray, K. N. C. The conservation equations for a non-equilibrium plasma. J. Fluid. Mech. 1964, 20, 659-72.
52. Wheatcraft, S. W.; Meerschaert, M. M. Fractional conservation of mass. Adv. Water. Resources. 2008, 31, 1377-81.
53. Hubbert, M. K. Darcy’s law and the field equations of the flow of underground fluids. Trans. AIME. 1956, 207, 222-39.
54. Wang, J.; Xie, H.; Wang, Y.; Ouyang, R. Distilling accurate descriptors from multi-source experimental data for discovering highly active perovskite OER catalysts. J. Am. Chem. Soc. 2023, 145, 11457-65.
57. Minsky, M.; Papert, S. A. Perceptrons: an introduction to computational geometry. MIT Press: 2017.
58. Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: comparison of trends in practice and research for deep learning. arXiv2018, arXiv:1811.03378. Available online: https://doi.org/10.48550/arXiv.1811.03378. (accessed 11 Apr 2025)
59. Baydin, A. G.; Pearlmutter, B. A.; Radul, A. A.; Siskind, J. M. Automatic differentiation in machine learning: a survey. arXiv2015, arXiv:1502.05767. Available online: https://doi.org/10.48550/arXiv.1502.05767. (accessed 11 Apr 2025)
60. Agrawal, A.; Choudhary, A. Deep materials informatics: applications of deep learning in materials science. MRS. Commun. 2019, 9, 779-92.
61. Permann, C. J.; Gaston, D. R.; Andrš, D.; et al. MOOSE: enabling massively parallel multiphysics simulation. SoftwareX 2020, 11, 100430.
62. Zhang, C.; Liu, X.; Chen, J.; Hu, X.; Guo, Y.; Cui, P. Study on uncertainty propagation analysis method in ablative thermal response calculation. J. Astronautics. 2020, 41, 1401-9. (in Chinese).
63. Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B. 1996, 58, 267-88.
66. Ye, S.; Senftle, T. P.; Li, M. Operator-induced structural variable selection for identifying materials genes. J. Am. Stat. Assoc. 2024, 119, 81-94.
67. Sandberg, J.; Voigtmann, T.; Devijver, E.; Jakse, N. Feature selection for high-dimensional neural network potentials with the adaptive group lasso. Mach. Learn. Sci. Technol. 2024, 5, 025043.
68. Wang, P.; Zhao, S.; Zhou, C.; et al. Simple formula learned via machine learning for creep rupture life prediction of high-temperature titanium alloys. J. Mater. Inf. 2024, 4, 24.
69. Fox, J.; Weisberg, S. An R companion to applied regression. Sage publications: 2018. https://uk.sagepub.com/en-gb/eur/an-r-companion-to-applied-regression/book246125. (accessed 11 Apr 2025).
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data

























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].