Nonlinear Hall effect in two-dimensional materials
Abstract
Symmetry is a cornerstone of condensed matter physics, fundamentally shaping the behavior of electronic systems and inducing the emergence of novel phenomena. The Hall effect, a key concept in this field, demonstrates how symmetry breaking, particularly of time-reversal symmetry, influences electronic transport properties. Recently, the nonlinear Hall effect has extended this understanding by generating a transverse voltage that modulates at twice the frequency of the driving alternating current without breaking time-reversal symmetry. This effect is closely tied to the symmetry and quantum geometric properties of materials, offering a new approach to probing the Berry curvature and quantum metric. Here, we provide a review of the theoretical insights and experimental advancements in the nonlinear Hall effect, particularly focusing on its realization in two-dimensional materials. We discuss the challenges still ahead, look at potential applications for devices, and explore how these ideas might apply to other nonlinear transport phenomena. By elucidating these aspects, this review aims to advance the understanding of nonlinear transport effects and their broader implications for future technologies.
Keywords
INTRODUCTION
Symmetry is foundational in condensed matter physics, guiding the understanding and prediction of material behaviors. It plays a crucial role in determining the properties of structural, electronic, optical, and magnetic systems[1–5]. By considering the symmetry, one can classify phases of matter, comprehend phase transitions, and predict the emergence of new quantum phenomena[6–9]. For example, in optics, symmetry dictates the selection rules for transitions and governs the behavior of light in various media[10,11]. In electronics, symmetry strongly affects the band structures of materials by modulating the band degeneracy, effective mass and topology, thus playing a significant role in determining electron transport properties[12–16]. The Hall effects, characterized by the emergence of a transverse voltage in response to a longitudinal current, exemplify the profound influence of symmetry, manifesting in diverse and distinctive forms. The conventional Hall effect arises from the breaking of time-reversal (T) symmetry under the influence of an external magnetic field, whereas the quantum Hall effect is marked by quantized conductance in the presence of strong magnetic field[17,18]. The anomalous Hall effect originates from intrinsic T symmetry breaking driven by magnetic order[19], while the spin Hall effect leverages spin-orbit coupling, notably without violating T symmetry[20].
The nonlinear Hall effect is a recently uncovered phenomenon characterized by the emergence of a Hall voltage that scales quadratically with the applied current. In non-magnetic systems, this effect arises exclusively from the breaking of parity inversion symmetry (P), without requiring the violation of time-reversal symmetry, thereby providing profound insights into the topological and symmetry characteristics of materials[21]. Furthermore, in magnetic systems, the realization of the nonlinear Hall effect, driven by the quantum metric, requires the simultaneous breaking of both P and T symmetries. Therefore, the nonlinear Hall effect serves as a novel probe for exploring quantum phases and is prevalent in a wide range of materials, particularly in two-dimensional (2D) systems, such as 2D Weyl semimetals and elemental materials[22–28]. Although nonlinear Hall effect is usually observed in materials with metallic features, He and Law's recent theoretical suggested that this effect can also occur in insulators when the driving frequency approaches the band gap[29]. This ability to generate a transverse voltage, regardless of whether the material is metallic or insulating and without requiring an external magnetic field, as depicted in Figure 1A, opens new possibilities for applications in electronic devices and sensors.
Figure 1. Advancements in the exploration of the nonlinear Hall response in various 2D systems. (A) Schematic of the measurement geometry of the second-order nonlinear Hall effect. (B and C) The nonlinear Hall response in 2D Weyl semimetals and 2D topological insulators with inherent symmetry breaking. (D and E) The nonlinear Hall response in heterostructures and moiré superlattices through structural engineering. (B) reprinted with permission[30], 2024, CC BY license. (D) reprinted with permission[27,31]. Copyright 2023, The American Association for the Advancement of Science and 2023, CC BY license. (E) reprinted with permission[32,33], 2021, CC BY license and 2022, CC BY license.
In this review, we initially introduce the fundamental symmetries underlying the nonlinear Hall effect, providing a theoretical framework to comprehend this phenomenon. Then the mechanisms and various factors resulting in this effect are discussed. Subsequently, experimental advancements in detecting the nonlinear Hall effect in 2D materials are explored, as illustrated in Figure 1B-E. This includes cases of inherent symmetry breaking in specific materials and instances resulting from structural engineering. Finally, we outline potential devices utilizing this effect and other nonlinear transport phenomena, highlighting promising avenues for future research and technological innovation.
FUNDAMENTAL SYMMETRIES
In electromagnetic phenomena, two fundamental symmetries play a crucial role: parity inversion and time-reversal symmetry. Parity inversion symmetry involves spatial inversion. It refers to the invariance of physical laws under inversion of spatial coordinates. Mathematically, this is represented as (
According to the Maxwell equations, a magnetic field
Figure 2. Fundamental symmetries for E and H. (A and B) H is an axial vector. It is odd under time-reversal and even under parity inversion. (C) The symmetry of two antiparallel magnetic fields; both P and T symmetries are broken but PT symmetry is preserved. (D and E) E is a polar vector. It is even under time-reversal and odd under parity inversion.
Based on the symmetry considerations outlined above, the T symmetry in the Hall effect is broken by applying a magnetic field[36,37]. Additionally, this symmetry framework elucidates the conditions required for the nonlinear Hall effect, in which the induced current J scales quadratically with the electric field E rather than linearly, represented as:
where
MECHANISMS UNDERLYING THE NONLINEAR HALL EFFECT
The nonlinear Hall effect arises from a rich interplay of fundamental symmetries that govern the behavior of charge carriers in materials. Through symmetry analysis, researchers have identified various mechanisms that can give rise to this effect. Among them, the quantum metric dipole and Berry curvature dipole are crucial, as they illustrate how the geometric properties of the band structure influence transport phenomena[21,26,38,39]. Additionally, disorder could also play an important role in the nonlinear Hall response by various mechanisms such as side-jump and skew scattering[40,41]. As a result, these factors create a diverse landscape for understanding and harnessing the nonlinear Hall effect across different materials.
Quantum metric dipole
In condensed matter physics, quantum geometry:
For the nonlinear Hall effect, the quantum metric is one of the indispensable points contributing to the second-order current response, whose conductivity tensor characterizes the second-order current response of the current J to E:
(
Summary of the scattering time
| Mechanism | Symmetry | |||
| P | T | PT | ||
| Quantum metric dipole[26] | ||||
| Berry curvature dipole[21] | ||||
| Side-jump[40] | ||||
| Skew scattering[40,47] | ||||
The nonlinear Hall effect induced by the quantum metric dipole arises in the presence of an electric field. The electron velocity under electric field
Recently, Gao et al. demonstrated that the electric field can introduce a gauge-invariant correction to the Berry connection:
As a result, the Berry curvature can be rewritten as
The third term represents an anomalous velocity that is proportional to the square of the electric field and is independent of the
where
When considering symmetries, the emergence of the quantum metric requires the breaking of both P and T symmetries[26]. In addition, PT symmetry eliminates the contributions from the Berry curvature dipole, as the Berry curvature is zero[21]. Consequently, a structure that violates both P and T symmetries while preserving PT symmetry provides an ideal setting for investigating the quantum metric dipole induced nonlinear Hall effect[26,27,49].
Berry curvature dipole
Besides the quantum metric dipole, the Berry curvature dipole can also give rise to the nonlinear transport[21,25]. The Berry curvature
where
The Berry curvature dipole induced nonlinear Hall effect can be derived from the Boltzmann equation under the relaxation time approximation,
where it is assumed that
The term
The term
Based on the current density formula
which represents the rectified current, and
which corresponds to the second harmonic current. Based on Eq.(1), the tensor of nonlinear Hall response is written as:
It is clear the
In this vein, we can understand the requirement of the nonlinear Hall response induced by the Berry curvature dipole more clearly based on the analyses of the symmetry. Firstly, under T symmetry, both the group velocity and Berry curvature reverse their signs, but their product remains unchanged, indicating the nonlinear Hall response can be observed with T symmetry. Secondly, under P symmetry, the group velocity reverses its sign, but the Berry curvature does not, resulting in a zero Berry curvature dipole moment. Therefore, to observe the nonlinear Hall effect, the P symmetry must be broken.
Besides the symmetries mentioned above, other symmetries significantly influence the nonlinear Hall effect. The chiral symmetry plays a pivotal role in the nonlinear Hall effect[55]. It refers to the absence of improper symmetries, such as inversion and mirror symmetries. The absence of these symmetries results in an inherent asymmetry, distinguishing between left- and right-handed configurations. The broken inversion symmetry, induced by chirality, ensures a finite valley-contrasting Berry curvature, which, in turn, gives rise to a Hall-like net transverse conductivity, contributing to the nonlinear Hall response[56]. Moreover, when chiral symmetry is broken, the nonlinear Hall current can attain quantization[57]. Beyond chiral symmetry, systems that break PT symmetry also manifest a third-order nonlinear Hall effect, driven by the Berry curvature quadrupole. PT symmetry enforces the vanishing of Berry curvature quadrupoles, so materials that break PT symmetry, such as bulk MnBi2Te4[58] and FeSn[59] under an external magnetic field, exhibit a third-order nonlinear Hall effect. The mirror symmetry and cyclic rotations symmetry also affect the nonlinear hall effect. Under
Side-jump and skew scattering
Besides the intrinsic mechanisms, disorder also plays an integral role in a variety of Hall effects, such as the extrinsic contributions of the anomalous, valley, and spin Hall effects[19,20,60,61]. In the case of the nonlinear Hall effect, the intrinsic mechanism plays a crucial role, but disorder-related still cannot be overlooked. This is because this effect inherently requires the Fermi energy to intersect with the energy bands, making disorder scattering inevitable at the Fermi surface. In fact, disorder plays a role even at leading order, contributing critically to the overall response[40,41].
Utilizing the Boltzmann equation:
where
Du et al. systematically classified the contributions to the nonlinear Hall response under the influence of disorder. Their work identifies three key components: the intrinsic contribution, the extrinsic side-jump scattering, and the skew scattering mechanisms[40].
The side-jump scattering occurs during the scattering of electrons off impurities or phonons in a material. When an electron scatters, its trajectory is deflected, not just by the usual scattering angle but also by an additional transverse displacement. The transverse displacement
where
On the other hand, skew scattering occurs when electrons are scattered asymmetrically due to spin-orbit interaction. The spin-orbit interaction causes the scattering to be asymmetric, meaning the probability of scattering to one side is different from the probability of scattering to the other side[63,64]. Over many scattering events, the asymmetry leads to a net transverse current, which causes the nonlinear Hall effect[65,66]. The skew scattering induced nonlinear Hall effect can also be separated into two parts:
and
where
In conclusion, the mechanisms governing the nonlinear Hall effect encompass the quantum metric dipole, the Berry curvature dipole, and disorder-induced phenomena such as side-jump and skew scattering. Both the quantum metric dipole and the Berry curvature dipole give rise to nonlinear Hall responses intrinsically linked to the quantum geometry of the system. Meanwhile, disorder-induced nonlinear Hall effects offer a valuable avenue for investigating disordered systems. These mechanisms manifest distinct experimental behaviors. Notably, the Berry curvature dipole exhibits a response that closely mirrors that of disorder-induced mechanisms, particularly due to its dependence on relaxation time. Importantly, the Berry curvature dipole is prohibited in systems exhibiting threefold rotational symmetry[67]. Under such conditions, the nonlinear Hall effect is primarily driven by disorder and the quantum metric dipole, with the two contributions distinguishable by their contrasting relaxation-time dependencies.
SYMMETRY BREAKING INDUCED NONLINEAR HALL EFFECT IN 2D MATERIALS
The 2D materials exhibit a range of intriguing physical properties arising from their unique structural and electronic characteristics[34,68–71]. Many of these materials possess intrinsic symmetry breaking[42,72,73], which gives rise to their emergent transport behaviors, including the nonlinear Hall effect. Beyond the intrinsic symmetry breaking, researchers can intentionally break the symmetry through structural engineering techniques, such as the creation of heterostructures and 2D moiré superlattices[74–77]. These engineered systems provide new avenues to explore and enhance the nonlinear Hall effect, leading to exciting potential applications in electronic and optoelectronic devices.
Intrinsic symmetry broken in 2D materials
The nonlinear Hall response is generally measured through a Hall-bar device [Figure 1A]. To detect this effect, an alternating current
The nonlinear Hall effect was initially observed in Td-WTe2, a 2D semimetal characterized by broken P symmetry[22,23]. Through the typical measurement on a Hall-bar device, Kang et al. measured the double-frequency voltage of the few-layer WTe2 at temperatures ranging from 2 to 100 K[22]. They found the transverse electric field with
Figure 3. Experimental investigations of the nonlinear Hall response in WTe2 and MnBi2Te4. (A) the
where
With further research into the nonlinear Hall effect, the mechanism of quantum metric dipole was proposed to induce the nonlinear Hall effect[39]. This mechanism is referred to as the intrinsic nonlinear Hall effect since the
as shown in Figure 3F, they found the predominant contribution to both the
Given the multitude of mechanisms that can induce the nonlinear Hall effect, an effective approach to classify them is essential. In experiments, one can apply the scaling law proposed by Du et al.[40]:
Here, the coefficients
In the limit
From the calculated values of
In addition, based on Eq. (24), since
For the nonlinear Hall effect induced by the quantum metric dipole, a similar scaling analysis can be conducted. Based on Eq. (25), the contributions to the nonlinear Hall effect can be categorized into two distinct mechanisms: one that is independent of the scattering time
Symmetry design through structure engineering
Due to the stringent symmetry requirements for the nonlinear Hall effect, the range of materials that can realize this effect is quite limited. Some of these materials require complex synthesis methods and may not even remain stable in air, which significantly restricts their practical applications[22,24]. Additionally, the electronic properties of these materials are strongly affected by their crystal structure and composition, making it difficult to modify them as desired[70,84], which reduces the ability to optimize the magnitude of the nonlinear Hall effect signals. Recently, some researchers have attempted to break the symmetry of materials through doping[85]. However, this approach has inherent limitations. The doping concentration is constrained, and achieving a controllable distribution of the dopants is often challenging. Significant emphasis has been placed on the study of oxide interfaces, where spontaneous symmetry breaking inherently fulfills the conditions required for the nonlinear Hall effect[86–88]. Likewise, there is growing emphasis on exploring heterostructures composed of 2D materials, where intentional symmetry breaking can be effectively achieved by stacking different materials[31,75,89,90]. Recent years have witnessed significant progress in the design and fabrication of heterostructures, opening new avenues for this research. Utilizing techniques such as mechanical exfoliation and the dry-transfer method[91,92], researchers can meticulously create 2D heterostructures tailored to specific experimental requirements. This innovative approach not only facilitates the investigation of fundamental physical phenomena but also paves the way for potential applications in next-generation devices, where engineered symmetry breaking may lead to novel functionalities.
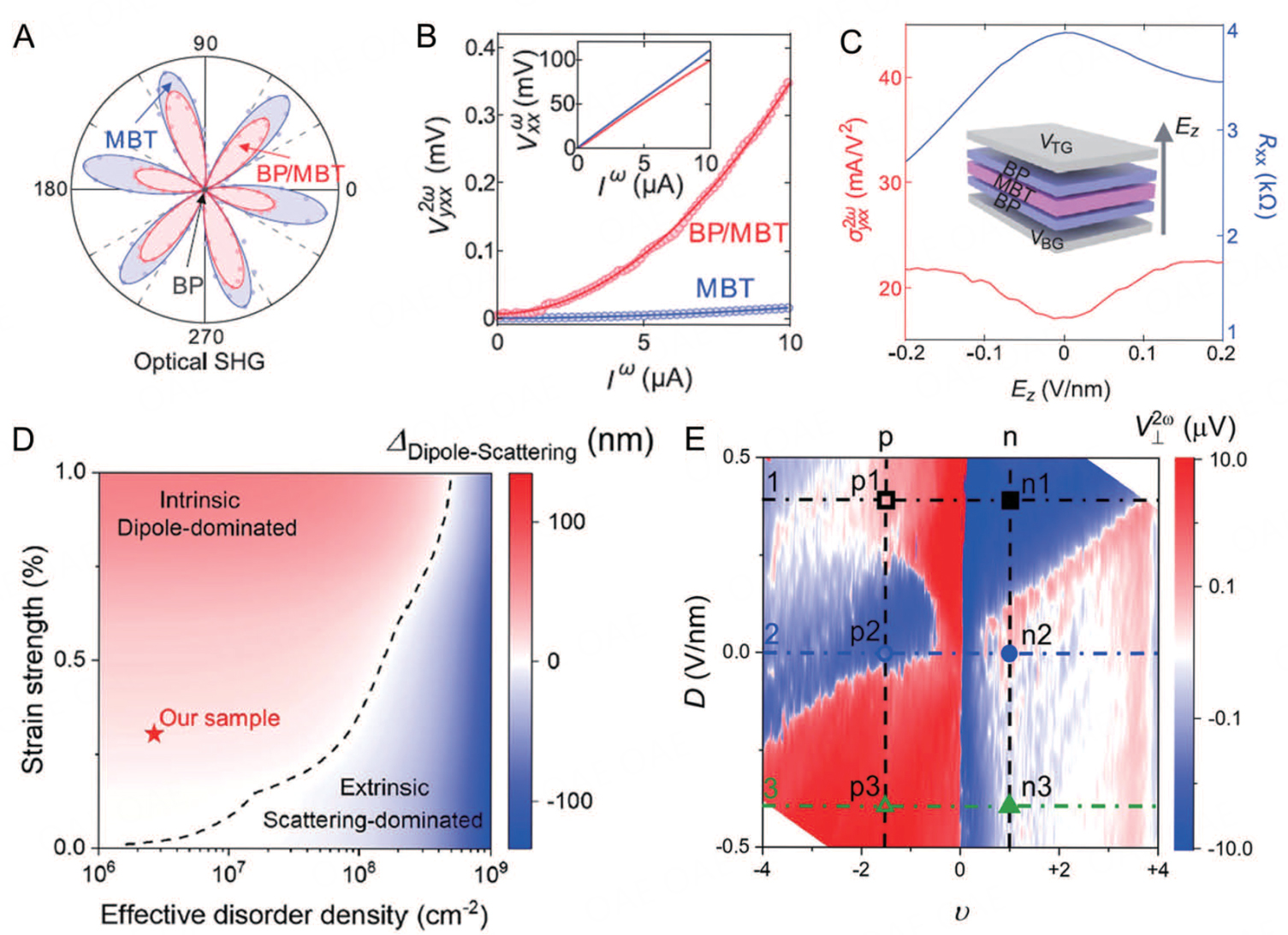
Through this structure engineering, Gao et al. investigated the nonlinear Hall effect in even layered MnBi2Te4 interfaced with black phosphorus (BP)[27]. The lattice of MnBi2Te4 has
Figure 4. Experimental studies of the nonlinear Hall response in topological antiferromagnetic heterostructure (BP/MnBi2Te4) and twisted bilayer graphene. (A) Optical second harmonic generation measurements of a 6 SLs MnBi2Te4 before and after being coupled with BP. (B) The
With the advancement of 2D van der Waals stacking technology, the fabrication of 2D moiré superlattices has become feasible through techniques such as tear-and-stack[94] and cut-and-stack[95] methods. Researchers have successfully synthesized 2D moiré superlattices in materials including twisted trilayer graphene[95–97], twisted bilayer boron nitride (tBN), and twisted WSe2-MoSe2 heterobilayers[98]. These structures exhibit intriguing physical properties, including superconductivity[97,99,100], topological phases[76,101] and correlated insulating states[102–104]. Furthermore, the spontaneous atomic reconstruction associated with these moiré patterns leads to symmetry breaking within the material, thereby facilitating the emergence of the nonlinear Hall effect.
Recently, Huang et al. detected a nonlinear Hall signal in high-mobility monolayer twisted graphene samples[93]. Two mechanisms for generating the nonlinear Hall effect in graphene superlattices have been proposed. As shown in Figure 4D, the Berry curvature dipole dominates in samples with high strain and low impurity concentration, whereas disorder dominates in samples with low strain and high impurity concentration. Additionally, the Berry curvature dipole can be effectively tuned by gate voltage, even allowing a change in the direction of the dipole [Figure 4E]. This study presents an efficient method to control and manipulate the amplitude and direction of the Berry curvature dipole, thereby enabling control over the nonlinear Hall response.
In addition to the 2D materials previously mentioned, the nonlinear Hall effect has been identified in a variety of other materials in recent years [Table 2]. The Weyl semimetals, such as MoTe2[105] and TaIrTe4[25], with a
Nonlinear Hall effect in various materials
| Materials | Mechanisms | Temperature (K) | Input current frequency (Hz) | Input current maximum (μA) | Output voltage maximum (μV) | |
| Weyl semimetals | Bilayer WTe2[23] | Berry curvature dipole | 10-100 | 10-1, 000 | 1 | 200 |
| Few-layer WTe2[22] | Berry curvature dipole & skew scattering | 1.8-100 | 17-137 | 600 | 25 | |
| Bilayer MoTe2[105] | Berry curvature dipole & skew scattering | 10-100 | 13.373-133.33 | 200 | 45 | |
| TaIrTe4[25] | Berry curvature dipole | 2-300 | 13.7-213.7 | 600 | 100 | |
| NbIrTe4[30] | Berry curvature dipole | 2-300 | 17.77-117.77 | 200 | 30 | |
| Rashba materials | BiTeBr[66] | Skew scattering | 300-350 | 7.777-277.77 | 5 | 100 |
| Dirac semimetals | BaMnSb2[106] | Berry curvature dipole | 200-400 | 17.777-117.77 | 100 | 250 |
| Elemental materials | Te[65] | Side-jump & skew scattering | 200-300 | 53.7-313.7 | 50 | 200 |
| Te[107] | Side-jump | 10-100 | 31 | 1 | 220 | |
| Bi[108] | Side-jump & skew scattering | 283-333 | 787 | 60 | 0.6 | |
| Topological insulators | MnBi2Te4[26] | Quantum metric dipole | 1.6-30 | 17.777-117.77 | 10 | 200 |
| Bi2Se3[67] | Skew scattering | 20-200 | 9-263 | 1,500 | 15 | |
| ZrTe5[109] | Berry curvature dipole | 2-100 | 17.777 | 200 | 10 | |
| Structure engineering | Strain tunable Monolayer WSe2[110] | Berry curvature dipole | 50-140 | 17.777 | 4.5 | 10 |
| Twisted bilayer WSe2[111] | Berry curvature dipole | 1.5-40 | 4.579 | 0.06 | 20,000 | |
| Twisted Bilayer Graphene[112] | Skew scattering | 1.7-80 | 13.777-33.777 | 5 | 1,000 | |
| hBN/graphene/hBN[112] | Skew scattering | 1.65-210 | 31 | 5 | 125 | |
| Twisted double bilayer graphene[83] | Berry curvature dipole | 1.5-25 | 18.03-177.81 | 0.2 | 60 | |
| Mn3Sn/Pt[49] | Quantum metric dipole | 5-400 | 10-80 | 5 | 40 | |
| BP/MnBi2Te4[27] | Quantum metric dipole | 1.8-30 | 17.77-1717.77 | 10 | 350 |
PROSPECTS
Other nonlinear transport effects
The nonlinear Hall effect typically involves a quadratic response of the longitudinal Hall voltage to the applied transverse current. However, in some materials, there could be higher-order responses in Hall effect. The second-order derivatives of the Berry connection polarizability could also induce the third-order nonlinear Hall effect. Analogous to the second-order nonlinear Hall effect, the third order nonlinear conductance can be expressed as[58]:
Distinct from the linear and second-order nonlinear Hall effects, the third-order Hall effect follows unique symmetry constraints and does not require broken T or P symmetry, making it a valuable tool for characterizing materials that preserve both symmetries[114].
The first observation of the third-order nonlinear Hall effect was made in MoTe2[115]. As depicted in Figure 5A, in the
Figure 5. The third-order nonlinear Hall effect in several materials. (A) b-c plane of few-layer
In addition to the higher order nonlinear Hall effect, the nonlinear spin Hall response can be realized through charge-to-spin conversion[120,121]. In thermally driven systems, the nonlinear response includes effects such as the nonlinear Nernst effect, the nonlinear Seebeck effect, and the nonlinear anomalous thermal Hall effect[122–125]. The planar Hall effect, unlike the traditional Hall effect, occurs when the Hall voltage, electric field, and magnetic field are coplanar[126–128]. The nonlinear planar Hall effect further introduces a higher-order response, where the transverse voltage scales nonlinearly with the applied current or magnetic field[93,129,130]. Collectively, these nonlinear transport phenomena offer rich opportunities for exploring new physics and developing innovative applications in science and technology.
Device applications
Due to its unique sensitivity to symmetry breaking and material properties, the nonlinear Hall effect offers applications in phase probing and the investigation of topological phenomena in condensed matter systems[131,132]. In twisted double bilayer graphene, the application of a perpendicular electric field can concurrently adjust both the valley Chern number and the Berry curvature dipole, offering a tunable platform to investigate topological transitions[113], as shown in Figure 6A-C. The Berry curvature dipole can also be tuned by strain[110,133] [Figure 6D]. This provides new ideas and methods for designing piezoelectric-like devices, such as strain sensors.
Figure 6. Device applications of the nonlinear Hall effect span diverse fields, including probing topological transitions, developing strain sensors, and creating wireless radiofrequency rectifiers. (A) Schematic of the nonlinear Hall measurement. (B) Band structures of the K valley for two different interlayer potential values, with the overlaid color representing the Berry curvature of the corresponding flat bands. (C) The variation in the Berry curvature dipole as a function of energy E at two different Fermi energies. (D) A strain sensor leveraging the nonlinear Hall response. (E) Wireless radiofrequency rectifier via the nonlinear Hall response. (A-C) reprinted with permission[113], 2022, CC BY license. (D) reprinted with permission[133], Copyright 2020, The American Physical Society. Panel E reprinted with permission[65], 2024, CC BY license.
Beyond its scientific significance in probing quantum geometry and crystalline symmetry, the nonlinear Hall effect holds substantial potential for practical applications, particularly in energy harvesting and rectifying devices[25,47,134], as shown in Figure 6E. Materials exhibiting the nonlinear Hall effect can function as wireless radiofrequency (RF) rectifiers operating without an external bias (battery-free), and in the absence of a magnetic field by utilizing a driving alternating current in place of an oscillating electromagnetic field[135]. For example, the use of materials such as TaIrTe4[25] and MnBi2Te4[27] in RF rectification has demonstrated cutoff frequencies reaching up to 5 GHz, which is sufficient to encompass the widely utilized 2.4 GHz Wi-Fi channel. Furthermore, BiTeBr-based rectifiers have exhibited RF rectification initiating at power levels as low as -15 dBm (0.03 mW), aligning closely with ambient RF power levels ranging from -20 to -10 dBm[66,136]. In addition, the rectified output in tellurium thin flakes can be significantly enhanced through the application of a gate voltage[65]. This class of Hall rectifiers, relying on the intrinsic material properties, effectively bypasses the limitations imposed by transition time and thermal voltage thresholds, presenting a promising solution for efficient, low-power energy conversion technologies[137].
PERSPECTIVE
The study of the nonlinear Hall response, which is rapidly advancing the condensed matter physics, has opened new frontiers within material science research, particularly in the realm of 2D systems. By leveraging the principles of symmetry, researchers have uncovered novel mechanisms that drive this effect, distinguishing it from traditional Hall phenomena[21,39,40]. The insights gained from these studies not only deepen our understanding of the interplay between symmetry and electronic properties, but also pave the way for innovative applications in electronic devices and sensors.
However, realizing practical devices based on the nonlinear Hall effect presents several challenges. First, the scale of most 2D materials exhibiting the nonlinear Hall effect is limited, with sizes typically restricted to a few tens of micrometers. This constraint poses a significant challenge to the development of large-scale, integrated applications leveraging the nonlinear Hall effect. Furthermore, although wireless RF rectifiers based on this effect can function without an external bias, their conversion efficiency remains low. Moreover, the nonlinear Hall effect weakens at higher frequencies due to the interplay with material relaxation times, further complicating its integration into existing technological frameworks.
Future research on the nonlinear Hall effect should strategically focus on advancing theoretical frameworks, driving material discovery, and addressing device scalability to fully realize its potential. Refining theoretical models to encompass higher-order nonlinear responses, quantum geometric effects, and the role of disorder is imperative for deepening our understanding of the underlying mechanisms. In parallel, identifying materials with pronounced nonlinear Hall effect responses, particularly those operational at high temperatures, is essential. Promising candidates include non-centrosymmetric 2D materials, topological semimetals, and moiré superlattices. Moreover, dynamic control of the nonlinear Hall effect through effective gating strategies, such as the modulation of the band structure through electric and optical fields[93,138,139], strain engineering[110], and chemical doping[85], will be key to tailoring device performance. Furthermore, achieving scalable fabrication of high-quality 2D materials is vital for the development of energy-harvesting devices that leverage the nonlinear Hall effect, propelling it from fundamental exploration to transformative applications.
CONCLUSION
In conclusion, the nonlinear Hall effect arises from diverse mechanisms, including contributions from the quantum metric and Berry curvature dipole, alongside skew scattering and side-jump effects, each uniquely shaping the nonlinear response. Experimentally, this effect has been extensively explored in 2D materials, encompassing intrinsic symmetry breaking in specific systems and engineered configurations, such as heterostructures and moiré superlattices. The ability to manipulate electronic responses without requiring an external magnetic field positions the nonlinear Hall effect as a transformative platform for next-generation electronic devices. Potential applications span highly efficient rectifiers, sensitive detectors, and innovative logic devices. Looking ahead, the nonlinear Hall effect is poised to serve as a cornerstone for the exploration of other nonlinear transport phenomena, offering vast opportunities for groundbreaking discoveries. The continued study of this phenomenon promises to deepen insights into condensed matter physics while paving the way for advanced technologies that capitalize on the unique electronic properties of 2D materials.
DECLARATIONS
Authors’ contributions
Made substantial contributions to conception and design of the study: Niu, W.; Fang, Y. W.
Writing: Wang, S.; Niu, W.; Fang, Y. W.
Availability of data and materials
Not applicable.
Financial support and sponsorship
The work carried out by Wang, S. and Niu, W. was supported by the Natural Science Foundation of Nanjing University of Posts and Telecommunications (NY222170).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2025.
REFERENCES
1. Rüter, C. E.; Makris, K. G.; El-Ganainy, R.; et al. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192-5.
2. Liu, L.; Zhao, T.; Lin, W.; et al. Symmetry breaking for current-induced magnetization switching. Appl. Phys. Rev. 2023, 10, 021319.
3. Dembowski, C.; Dietz, B.; Graf, H. D.; et al. Observation of a chiral state in a microwave cavity. Phys. Rev. Lett. 2003, 90, 034101.
4. Zhang, X.; Zhu, T.; Zhang, S.; et al. Light-induced giant enhancement of nonreciprocal transport at KTaO3-based interfaces. Nat. Commun. 2024, 15, 2992.
5. Li, C. N.; Liang, H. P.; Zhao, B. Q.; Wei, S. H.; Zhang, X. Machine learning assisted crystal structure prediction made simple. J. Mater. Inf. 2024, 4, 15.
6. Ji, W.; Wen, X. G. Categorical symmetry and noninvertible anomaly in symmetry-breaking and topological phase transitions. Phys. Rev. Res. 2020, 2, 033417.
8. Li, C.; Wang, R.; Zhang, S.; et al. Observation of giant non-reciprocal charge transport from quantum hall states in a topological insulator. Nat. Mater. 2024, 23, 1208-13.
9. Zhao, H. J.; Chen, P.; Paillard, C.; et al. Large spin splittings due to the orbital degree of freedom and spin textures in a ferroelectric nitride perovskite. Phys. Rev. B. 2020, 102, 041203.
10. Brunschwig, B. S.; Creutz, C.; Surin, N. Optical transitions of symmetrical mixed-valence systems in the class Ⅱ-Ⅲ transition regime. Chem. Soc. Rev. 2000, 31, 168-84.
11. Chen, Z.; Qiu, H.; Cheng, X.; et al. Defect-induced helicity dependent terahertz emission in Dirac semimetal PtTe2 thin films. Nat. Commun. 2024, 15, 2605.
12. Niu, W.; Fang, Y. W.; Liu, R.; et al. Fully optical modulation of the two-dimensional electron gas at the γ-Al2O3/SrTiO3 interface. J. Phys. Chem. Lett. 2022, 13, 2976-85.
13. Niu, W.; Zhang, Y.; Gan, Y.; et al. Giant tunability of the two-dimensional electron gas at the interface of γ-Al2O3/SrTiO3γ-Al2O3/SrTiO3. Nano. Lett. 2017, 17, 6878-85.
14. Hu, L.; Luo, Y.; Fang, Y.; et al. High thermoelectric performance through crystal symmetry enhancement in triply doped diamondoid compound Cu2SnSe3. Adv. Energy. Mater. 2021, 11, 2100661.
15. Hu, L.; Fang, Y. W.; Qin, F.; et al. High thermoelectric performance enabled by convergence of nested conduction bands in Pb7Bi4Se13 with low thermal conductivity. Nat. Commun. 2021, 12, 105.
16. Zheng, D.; Fang, Y. W.; Zhang, S.; et al. Berry phase engineering in SrRuO3/SrIrO3/SrTiO3 superlattices induced by band structure reconstruction. ACS. Nano. 2021, 15, 5086-95.
17. Stormer, H. L. Nobel lecture: The fractional quantum hall effect. Rev. Mod. Phys. 1999, 71, 875-900.
19. Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A. H.; Ong, N. P. Anomalous hall effect. Rev. Mod. Phys. 2010, 82, 1539-92.
20. Sinova, J.; Valenzuela, S. O.; Wunderlich, J.; Back, C.; Jungwirth, T. Spin hall effects. Rev. Mod. Phys. 2015, 87, 1213-60.
21. Sodemann, I.; Fu, L. Quantum nonlinear hall effect induced by Berry curvature dipole in time-reversal invariant materials. Phys. Rev. Lett. 2015, 115, 216806.
22. Kang, K.; Li, T.; Sohn, E.; Shan, J.; Mak, R. F. Nonlinear anomalous hall effect in few-layer WTe2. Nat. Mater. 2019, 18, 324-8.
23. Ma, Q.; Xu, S. Y.; Shen, H.; et al. Observation of the nonlinear hall effect under time-reversal-symmetric conditions. Nature 2019, 565, 337-42.
24. Tiwari, A.; Chen, F.; Zhong, S.; et al. Giant c-axis nonlinear anomalous hall effect in Td-MoTe2 and WTe2. Nat. Commun. 2021, 12, 2049.
25. Kumar, D.; Hsu, C. H.; Sharma, R.; et al. Room-temperature nonlinear hall effect and wireless radiofrequency rectification in Weyl semimetal TaIrTe4. Nat. Nanotechnol. 2021, 16, 421-5.
26. Wang, N.; Kaplan, D.; Zhang, Z.; et al. Quantum-metric-induced nonlinear transport in a topological antiferromagnet. Nature 2023, 621, 487-92.
27. Gao, A.; Liu, Y. F.; Qiu, J. X.; et al. Quantum metric nonlinear hall effect in a topological antiferromagnetic heterostructure. Science 2023, 381, 181-6.
28. Rostami, H.; Juricic, V. Probing quantum criticality using nonlinear hall effect in a metallic Dirac system. Phys. Rev. Res. 2020, 2, 013069.
29. He, W. Y.; Law, K.T. Nonlinear hall effect in insulators. arxiv2024, 2411.07456. Available from: https://arxiv.org/abs/2411.07456 [Last accessed on 11 Apr 2024].
30. Lee, J. E.; Wang, A.; Chen, S.; et al. Spin-orbit-splitting-driven nonlinear hall effect in NbIrTe4. Nat. Commun. 2024, 15, 3971.
31. Duan, S.; Qin, F.; Chen, P.; et al. Berry curvature dipole generation and helicity-to-spin conversion at symmetry-mismatched heterointerfaces. Nat. Nanotechnol. 2023, 18, 867-74.
32. He, Z.; Weng, H. Giant nonlinear hall effect in twisted bilayer WTe2. NPJ. Quantum. Mater. 2021, 6, 101.
33. Hu, J. X.; Zhang, C. P.; Xie, Y. M.; Law, K. Nonlinear hall effects in strained twisted bilayer WSe2. Commun. Phys. 2022, 5, 255.
34. Gao, A.; Liu, Y. F.; Hu, C.; et al. Layer hall effect in a 2D topological axion antiferromagnet. Nature 2021, 595, 521-5.
36. Klitzing, K.; Dorda, G.; Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 1980, 45, 494-7.
37. Yasuda, K.; Wakatsuki, R.; Morimoto, T.; et al. Geometric hall effects in topological insulator heterostructures. Nat. Phys. 2016, 12, 555-9.
38. Gao, Y.; Yang, S. A.; Niu, Q. Field induced positional shift of Bloch electrons and its dynamical implications. Phys. Rev. Lett. 2014, 112, 166601.
39. Wang, C.; Gao, Y.; Xiao, D. Intrinsic nonlinear hall effect in antiferromagnetic tetragonal CuMnAs. Phys. Rev. Lett. 2021, 127, 277201.
40. Du, Z.; Wang, C.; Li, S.; et al. Disorder-induced nonlinear hall effect with time-reversal symmetry. Nat. Commun. 2019, 10, 3047.
41. Du, Z.; Wang, C.; Sun, H. P.; et al. Quantum theory of the nonlinear hall effect. Nat. Commun. 2021, 12, 5038.
42. Tokura, Y.; Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 2018, 9, 3740.
43. Provost, J.; Vallee, G. Riemannian structure on manifolds of quantum states. Commun. Math. Phys. 1980, 76, 289-301.
44. Tsirkin, S.; Souza, I. On the separation of hall and ohmic nonlinear responses. SciPost. Phys. Core. 2022, 5, 039.
45. Holder, T.; Kaplan, D.; Yan, B. Consequences of time-reversal-symmetry breaking in the light-matter interaction: berry curvature, quantum metric, and diabatic motion. Phys. Rev. Res. 2020, 2, 033100.
46. Watanabe, H.; Yanase, Y. Nonlinear electric transport in odd-parity magnetic multipole systems: application to Mn-based compounds. Phys. Rev. Res. 2020, 2, 043081.
47. Isobe, H.; Xu, S. Y.; Fu, L. High-frequency rectification via chiral Bloch electrons. Sci. Adv. 2020, 6, eaay2497.
48. Liu, H.; Zhao, J.; Huang, Y. X.; et al. Intrinsic second-order anomalous hall effect and its application in compensated antiferromagnets. Phys. Rev. Lett. 2021, 127, 277202.
49. Han, J.; Uchimura, T.; Araki, Y.; et al. Room-temperature flexible manipulation of the quantum-metric structure in a topological chiral antiferromagnet. Nat. Phys. 2024, 20, 1110-7.
50. Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A. 1984, 392, 45-57.
51. Xiao, D.; Chang, M. C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959-2007.
52. Bohm, A.; Mostafazadeh, A.; Koizumi, H.; Niu, Q.; Zwanziger, J. The Geometric phase in quantum systems: foundations, mathematical concepts, and applications in molecular and condensed matter physics. Springer Science & Business Media; 2013.
54. Low, T.; Jiang, Y.; Guinea, F. Topological currents in black phosphorus with broken inversion symmetry. Phys. Rev. B. 2015, 92, 235447.
55. Joseph, N. B.; Bandyopadhyay, A.; Narayan, A. Chirality-Tunable nonlinear hall effect. Chem. Mater. 2024, 36, 8602-12.
56. Zhu, H.; Yakobson, B. L. Creating chirality in the nearly two dimensions. Nat. Mater. 2024, 23, 316-22.
57. Peshchentseva, N.; Felser, C.; Zhang, Y. Quantized nonlinear hall effect from chiral monopole. Phys. Rev. B. 2024, 110, 155143.
58. Li, H.; Zhang, C.; Zhou, C.; et al. Quantum geometry quadrupole-induced third-order nonlinear transport in antiferromagnetic topological insulator MnBi2Te4. Nat. Commun. 2024, 15, 7779.
59. Sankar, S.; Liu, R.; Zhang, C. P.; et al. Experimental evidence for a berry curvature quadrupole in an antiferromagnet. Phys. Rev. X. 2024, 14, 021046.
60. Mak, K. F.; McGill, K. L.; Park, J.; McEuen, P. L. The valley hall effect in MoS2 transistors. Science 2014, 344, 1489-92.
61. Xu, C.; Moore, J. E. Stability of the quantum spin hall effect: effects of interactions, disorder, and Z2 topology. Phys. Rev. B. 2006, 73, 045322.
62. Berger, L. Side-jump mechanism for the hall effect of ferromagnets. Phys. Rev. B. 1970, 2, 4559-66.
65. Cheng, B.; Gao, Y.; Zheng, Z.; et al. Giant nonlinear hall and wireless rectification effects at room temperature in the elemental semiconductor tellurium. Nat. Commun. 2024, 15, 5513.
66. Lu, X. F.; Zhang, C. P.; Wang, N.; et al. Nonlinear transport and radio frequency rectification in BiTeBr at room temperature. Nat. Commun. 2024, 15, 245.
67. He, P.; Isobe, H.; Zhu, D.; et al. Quantum frequency doubling in the topological insulator Bi2Se3. Nat. Commun. 2021, 12, 698.
68. Novoselov, K. S.; Geim, A. K.; Morozov, S. V.; et al. Electric field effect in atomically thin carbon films. Science 2004, 306, 666-9.
69. Yang, H.; Valenzuela, S. O.; Chshiev, M.; et al. Two-dimensional materials prospects for non-volatile spintronic memories. Nature 2022, 606, 663-73.
70. Li, X.; Tao, L.; Chen, Z.; et al. Graphene and related two-dimensional materials: structure-property relationships for electronics and optoelectronics. Appl. Phys. Rev. 2017, 4, 021306.
71. Chia, X.; Pumera, M. Characteristics and performance of two-dimensional materials for electrocatalysis. Nat. Catal. 2018, 1, 909-21.
72. Zhang, Z.; Wang, N.; Cao, N.; et al. Controlled large non-reciprocal charge transport in an intrinsic magnetic topological insulator MnBi2Te4. Nat. Commun. 2022, 13, 6191.
73. Yasuda, K.; Morimoto, T.; Yoshimi, R.; et al. Large non-reciprocal charge transport mediated by quantum anomalous hall edge states. Nat. Nanotechnol. 2020, 15, 831-5.
74. Dean, C. R.; Wang, L.; Maher, P.; et al. Hofstadter's butterfly and the fractal quantum hall effect in moire superlattices. Nature 2013, 497, 598-602.
75. Novoselov, K. S.; Mishchenko, A.; Carvalho, A.; Castro Neto, A. 2D materials and van der Waals heterostructures. Science 2016, 353, aac9439.
76. Tong, Q.; Yu, H.; Zhu, Q.; et al. Topological mosaics in moire superlattices of van der Waals heterobilayers. Nat. Phys. 2017, 13, 356-62.
77. Finney, N. R.; Yankowitz, M.; Muraleetharan, L.; et al. Tunable crystal symmetry in graphene-boron nitride heterostructures with coexisting moire superlattices. Nat. Nanotechnol. 2019, 14, 1029-34.
78. Meng, K.; Li, Z.; Gao, Z.; et al. Gate-tunable berry curvature in van der Waals itinerant ferromagnetic CrTe. InfoMat 2024, 6, e12524.
79. Tian, Y.; Ye, L.; Jin, X. Proper scaling of the anomalous hall effect. Phys. Rev. Lett. 2009, 103, 087206.
80. Liu, E.; Sun, Y.; Kumar, N.; et al. Giant anomalous hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 2018, 14, 1125-31.
81. Deng, Y.; Yu, Y.; Shi, M. Z.; et al. Quantum anomalous hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020, 367, 895-900.
82. Gao, A.; Chen, S. W.; Ghosh, B.; et al. An antiferromagnetic diode effect in even-layered MnBi2Te4. Nat. Electron. 2024, 7, 751-9.
83. He, P.; Koon, G. K. W.; Isobe, H.; et al. Graphene moire superlattices with giant quantum nonlinearity of chiral Bloch electrons. Nat. Nanotechnol. 2022, 17, 378-83.
84. Zhang, K. X.; Ju, H.; Kim, H.; et al. Broken inversion symmetry in van der Waals topological ferromagnetic metal iron germanium telluride. Adv. Mater. 2024, 36, 2312824.
85. Wang, S.; Li, X.; Zhang, H.; et al. Nonlinear Hall effect and scaling law in Sb-doped topological insulator MnBi4Te7. Appl. Phys. Lett. 2024, 124, 153102.
86. Lesne, E.; Saglam, Y. G.; Battilomo, R.; et al. Designing spin and orbital sources of Berry curvature at oxide interfaces. Nat. Mater. 2023, 22, 576-82.
87. Trama, M.; Cataudella, V.; Perroni, C.; Romeo, F.; Citro, R. Gate tunable anomalous hall effect: berry curvature probe at oxides interfaces. Phys. Rev. B. 2022, 106, 075430.
88. Groenendijk, D. J.; Autieri, C.; van Thiel, T. C.; et al. Berry phase engineering at oxide interfaces. Phys. Rev. Res. 2020, 2, 023404.
89. Yankowitz, M.; Ma, Q.; Jarillo-Herrero, P.; LeRoy, B. J. van der Waals heterostructures combining graphene and hexagonal boron nitride. Nat. Rev. Phys. 2019, 1, 112-25.
90. Li, Z.; Huang, J.; Zhou, L.; et al. An anisotropic van der Waals dielectric for symmetry engineering in functionalized heterointerfaces. Nat. Commun. 2023, 14, 5568.
91. Wang, L.; Meric, I.; Huang, P.; et al. One-dimensional electrical contact to a two-dimensional material. Science 2013, 342, 614-7.
92. Kinoshita, K.; Moriya, R.; Onodera, M.; et al. Dry release transfer of graphene and few-layer h-BN by utilizing thermoplasticity of polypropylene carbonate. npj. 2D. Mater. Appl. 2019, 3, 22.
93. Huang, M.; Wu, Z.; Zhang, X.; et al. Intrinsic nonlinear Hall effect and gate-switchable Berry curvature sliding in twisted bilayer graphene. Phys. Rev. Lett. 2023, 131, 066301.
94. Kim, K.; Yankowitz, M.; Fallahazad, B.; et al. van der Waals heterostructures with high accuracy rotational alignment. Nano. Lett. 2016, 16, 1989-95.
95. Saito, Y.; Ge, J.; Watanabe, K.; Taniguchi, T.; Young, A. F. Independent superconductors and correlated insulators in twisted bilayer graphene. Nat. Phys. 2020, 16, 926-30.
96. Tian, H.; Gao, X.; Zhang, Y.; et al. Evidence for Dirac flat band superconductivity enabled by quantum geometry. Nature 2023, 614, 440-4.
97. Park, J. M.; Cao, Y.; Watanabe, K.; Taniguchi, T.; Jarillo-Herrero, P. Tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene. Nature 2021, 590, 249-55.
98. McGilly, L. J.; Kerelsky, A.; Finney, N. R.; et al. Visualization of moire superlattices. Nat. Nanotechnol. 2020, 15, 580-4.
99. Qiu, D.; Gong, C.; Wang, S.; et al. Recent advances in 2D superconductors. Adv. Mater. 2021, 33, 2006124.
100. Balents, L.; Dean, C. R.; Efetov, D. K.; Young, A. F. Superconductivity and strong correlations in moire flat bands. Nat. Phys. 2020, 16, 725-33.
102. Xu, Y.; Liu, S.; Rhodes, D. A.; et al. Correlated insulating states at fractional fillings of moire superlattices. Nature 2020, 587, 211-8.
103. Huang, X.; Wang, T.; Miao, S.; et al. Correlated insulating states at fractional fillings of the WS2/WSe2 moire lattice. Nat. Phys. 2021, 17, 715-9.
104. Andrei, E. Y.; Efetov, D. K.; Jarillo-Herrero, P.; et al. The marvels of moire materials. Nat. Rev. Mater. 2021, 6, 201-6.
105. Ma, T.; Chen, H.; Yananosc, K.; et al. Growth of bilayer MoTe2 single crystals with strong non-linear Hall effect. Nat. Commun. 2022, 13, 5465.
106. Min, L.; Tan, H.; Xie, Z.; et al. Strong room-temperature bulk nonlinear hall effect in a spin-valley locked Dirac material. Nat. Commun. 2023, 14, 364.
107. Suarez-Rodriguez, M.; Martin-Garcia, B.; Skowronski, W.; et al. Odd nonlinear conductivity under spatial inversion in chiral tellurium. Phys. Rev. Lett. 2021, 132, 046303.
108. Makushko, P.; Kovalev, S.; Zabila, Y.; et al. A tunable room-temperature nonlinear Hall effect in elemental bismuth thin films. Nat. Electron. 2024, 7, 207-15.
109. Wang, N.; You, J. Y.; Wang, A.; et al. Non-centrosymmetric topological phase probed by non-linear Hall effect. Natl. Sci. Rev. 2024, 11, nwa4103.
110. Qin, M. S.; Zhu, P. F.; Ye, X. G.; et al. Strain tunable Berry curvature dipole, orbital magnetization and nonlinear Hall effect in WSe2 monolayer. Chin. Phys. Lett. 2021, 38, 017301.
111. Huang, M.; Wu, Z.; Hu, J.; et al. Giant nonlinear hall effect in twisted bilayer WSe2. Natl. Sci. Rev. 2023, 10, nwac232.
112. Duan, J.; Jian, Y.; Gao, Y.; et al. Giant second-order nonlinear hall effect in twisted bilayer graphene. Phys. Rev. Lett. 2022, 129, 186801.
113. Sinha, S.; Adak, P. C.; Chakraborty, A.; et al. Berry curvature dipole senses topological transition in a moire superlattice. Nat. Phys. 2022, 18, 765-70.
114. Ye, X. G.; Zhu, P. F.; Xu, W. Z.; et al. Orbital polarization and third-order anomalous Hall effect in WTe2. Phys. Rev. B. 2022, 106, 045414.
115. Lai, S.; Liu, H.; Zhang, Z.; et al. Third-order nonlinear Hall effect induced by the Berry-connection polarizability tensor. Nat. Nanotechnol. 2021, 16, 869-73.
116. Wang, C.; Xiao, R. C.; Liu, H.; et al. Room-temperature third-order nonlinear Hall effect in Weyl semimetal TaIrTe4. Natl. Sci. Rev. 2022, 9, nwac020.
117. He, P.; Isobe, H.; Koon, G. K. W.; et al. Third-order nonlinear hall effect in a quantum Hall system. Nat. Nanotechnol. 2024, 19, 1460-5.
118. Chen, Z. H.; Liao, X.; Dong, J. W.; et al. Charge density wave modulated third-order nonlinear Hall effect in 1 T-VSe2 nanosheets. Phys. Rev. B. 2024, 110, 235135.
119. Li, S.; Wang, X.; Yang, Z.; et al. Giant third-order nonlinear Hall effect in misfit layer compound (SnS)1.17(NbS2)3. ACS. Appl. Mater. Interfaces. 2024, 16, 9.
120. Hamamoto, K.; Ezawa, M.; Kim, K. W.; Morimoto, T.; Nagaosa, N. Nonlinear spin current generation in noncentrosymmetric spin-orbit coupled systems. Phys. Rev. B. 2017, 95, 224430.
121. Araki, Y. Strain-induced nonlinear spin hall effect in topological Dirac semimetal. Sci. Rep. 2018, 8, 15236.
122. Zeng, C.; Nandy, S.; Taraphder, A.; Tewari, S. Nonlinear nernst effect in bilayer WTe2. Phys. Rev. B. 2019, 100, 245102.
123. Zeng, C.; Nandy, S.; Tewari, S. Fundamental relations for anomalous thermoelectric transport coefficients in the nonlinear regime. Phys. Rev. Res. 2020, 2, 032066.
124. Nakai, R.; Nagaosa, N. Nonreciprocal thermal and thermoelectric transport of electrons in noncentrosymmetric crystals. Phys. Rev. B. 2019, 99, 115201.
125. Yu, X. Q.; Zhu, Z. G.; You, J. S.; Low, T.; Su, G. Topological nonlinear anomalous Nernst effect in strained transition metal dichalcogenides. Phys. Rev. B. 2019, 99, 201410.
126. Kumar, N.; Guin, S. N.; Felser, C.; Shekhar, C. Planar hall effect in the Weyl semimetal GdPtBi. Phys. Rev. B. 2018, 98, 041103.
128. Tang, H.; Kawakami, R.; Awschalom, D.; Roukes, M. Giant planar Hall effect in epitaxial (Ga, Mn) as devices. Phys. Rev. Lett. 2003, 90, 107201.
129. He, P.; Zhang, S. S. L.; Zhu, D.; et al. Nonlinear planar Hall effect. Phys. Rev. Lett. 2019, 123, 016801.
130. Rao, W.; Zhou, Y. L.; Wu, Y. J.; Duan, H. J.; Deng, M. X.; et al. Theory for linear and nonlinear planar hall effect in topological insulator thin films. Phys. Rev. B. 2021, 103, 155415.
131. Xiao, J.; Wang, Y.; Wang, H.; et al. Berry curvature memory through electrically driven stacking transitions. Nat. Phys. 2020, 16, 1028-34.
132. Shao, D. F.; Zhang, S. H.; Gurung, G.; Yang, W.; Tsymbal, E. Y. Nonlinear anomalous hall effect for neel vector detection. Phys. Rev. Lett. 2020, 124, 067203.
133. Xiao, R. C.; Shao, D. F.; Zhang, Z. Q.; Jiang, H. Two-dimensional metals for piezoelectriclike devices based on Berry-curvature dipole. Phys. Rev. Appl. 2020, 13, 044014.
134. Zhang, Y.; Fu, L. Terahertz detection based on nonlinear hall effect without magnetic field. Proc. Natl. Acad. Sci. USA. 2021, 118, e2100736118.
135. Suarez-Rodriguez, M.; Martin-Garcia, B.; Skowronski, W.; et al. Microscale chiral rectennas for energy harvesting. Adv. Mater. 2024, 2400729.
136. Muhammad, S.; Tiang, J. J.; Wong, S. K.; et al. Harvesting systems for RF energy: trends, challenges, techniques, and tradeoffs. Electronics 2022, 11, 959.
137. Suarez-Rodriguez, M.; Juan, F. D.; Souza, I.; et al. Non-linear transport in non-centrosymmetric systems: from fundamentals to applications. arXiv2024, 2412.05253. Available from: https://arxiv.org/abs/2412.05253 [Last accessed on 11 Apr 2024].
138. Qin, F.; Shen, R.; Lee, C. H. Light-enhanced nonlinear hall effect. Commun. Phys. 2024, 7, 368.
139. Qin, F.; Shen, R.; Lee, C. H. Nonlinear Hall effects with an exceptional ring. arXiv2024, 2411.06509. Available from: http://dx.doi.org/10.48550/arXiv.2411.06509 [Last accessed on 11 Apr 2024].
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Data & Comments
Data

























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].