Nonlinear Hall effect in two-dimensional materials

Quantum metric dipole

In condensed matter physics, quantum geometry: $$ Q_{n}^{\mu v}=-\frac{i}{2}\Omega_{n}^{\mu v}+g_{n}^{\mu v} $$ plays a significant role in understanding various phenomena, especially those related to the electronic properties of materials^[42,43]. The quantum geometry can typically be divided into two main components: the imaginary part is Berry curvature, which describes the phase difference between two quantum states. The real component is the quantum metric, delineating the amplitude difference between them. Both of these geometric quantities are crucial to determining the behavior of electrons in various nonlinear transport phenomena^[21,39].

For the nonlinear Hall effect, the quantum metric is one of the indispensable points contributing to the second-order current response, whose conductivity tensor characterizes the second-order current response of the current J to E:

($$ \alpha $$, $$ \beta $$ and $$ \gamma $$ are Cartesian indices)^[21,39]. $$ \sigma $$ can be divided into two components: the Ohmic component and the Hall component^[44]. The Ohmic component comprises a Drude conductivity of second-order, which depends on the relaxation time $$ \tau $$^[45,46]. In contrast, the Hall component contains a $$ \tau $$ independent term^[38]. Based on the $$ \sigma-\tau $$ dependencies, the contribution of the second-order nonlinear Hall effect is able to be separated into intrinsic ($$ \tau $$-independent) and extrinsic ($$ \tau $$-dependent) components^[38,40]. It is noteworthy that, although the Berry curvature dipole actually depends on the relaxation time, it is generally regarded as the intrinsic contribution in research^[40]. On the other hand, disorder-related side-jump and skew scattering are normally attributed to the extrinsic mechanisms [Table 1].

The nonlinear Hall effect induced by the quantum metric dipole arises in the presence of an electric field. The electron velocity under electric field $$ \mathit{\boldsymbol{E}} $$ consists of two contributions, the group velocity, and the anomalous velocity due to the Berry curvature:

Recently, Gao et al. demonstrated that the electric field can introduce a gauge-invariant correction to the Berry connection: $$ A^{\mathit{\boldsymbol{E}}}(\mathit{\boldsymbol{k}})=G(\mathit{\boldsymbol{k}})\mathit{\boldsymbol{E}} $$, where $$ G(\mathit{\boldsymbol{k}}) $$ is the Berry connection polarizability tensor^[38], defined as

As a result, the Berry curvature can be rewritten as $$ {\widetilde{\Omega}}=\Omega+\nabla_{k}\times A^{\mathit{\boldsymbol{E}}}(\mathit{\boldsymbol{k}}) $$. Thus the electric velocity becomes

The third term represents an anomalous velocity that is proportional to the square of the electric field and is independent of the $$ \tau $$. Therefore, it contributes to the intrinsic nonlinear Hall effect. Based on Eq.(1), the intrinsic nonlinear Hall tensor is^[48]:

$$ G_{n}^{jk} $$ respresents the Berry connection polarizability in the n-band situation. In the simplified two-band scenario, the Berry connection polarizability $$ G_{n}^{jk} $$ simplifies as:

where $$ g_{n}^{jk} $$ is the quantum metric, and it is related to the Berry connection for non-diagonal terms. The quantum metric dipole, which characterizes the influence of the quantum geometry on transport phenomena, is given by the product of the group velocity and the quantum metric: $$ v_{n}^{i}g_{n}^{jk} $$, reflecting the spatial variation of the quantum states in momentum space.

When considering symmetries, the emergence of the quantum metric requires the breaking of both P and T symmetries^[26]. In addition, PT symmetry eliminates the contributions from the Berry curvature dipole, as the Berry curvature is zero^[21]. Consequently, a structure that violates both P and T symmetries while preserving PT symmetry provides an ideal setting for investigating the quantum metric dipole induced nonlinear Hall effect^[26,27,49].

Berry curvature dipole

Besides the quantum metric dipole, the Berry curvature dipole can also give rise to the nonlinear transport^[21,25]. The Berry curvature $$ \Omega $$ can be viewed as an effective magnetic field in the parameter space (e.g., momentum space), which has been recognized as the origin of various novel electronic phenomena^[19,50–53]. In the linear Hall effect, the Hall conductivity is defined as

where $$ f_{0} $$ is the Fermi distribution, n is the dimension, and $$ \varepsilon_{abc} $$ is the Levi-Civita symbol^[35]. The Berry curvature enables the calculation of the intrinsic anomalous Hall effect^[19,53], which is invariant under P symmetry but changes its sign under T symmetry. Therefore, in systems with T symmetry, the positive and negative momentum contributions cancel out during integration, resulting in zero Hall conductivity. To achieve non-zero Hall conductivity, the T symmetry must be broken by an external magnetic field or internal magnetization of the material.

The Berry curvature dipole induced nonlinear Hall effect can be derived from the Boltzmann equation under the relaxation time approximation, $$ -e\tau E_{a}\partial_{a}f+\tau \partial_{t}f=f_{0}-f $$, where $$ E_{a} $$ is the electric field and $$ f $$ is the distribution function. The electric field is considered to take the form $$ E_{c}(t)={\rm Re}\{\varepsilon_{c}e^{ei\omega t}\} $$^[21]. The distribution function can be expanded up to second order in terms of the electric field: $$ f=f_{0}+f_{1}+f_{2} $$. Substituting this expansion into the Boltzmann equation leads to:

where it is assumed that $$ \partial_{t}f_{0}=0 $$. This simplifies to:

The term $$ f_{1} $$ could be separated into two parts as follows: $$ f_{1}=f_{1}^{\omega}e^{i\omega t}+f_{1}^{-\omega}e^{-i\omega t} $$. Taking $$ f_{1} $$ into Eq.(10), it is found that:

The term $$ f_{2} $$ can be rewritten as: $$ f_{2}=f_{2}^{2\omega+}e^{i2\omega t}+f_{2}^{0+}+f_{2}^{0-}+f_{2}^{2\omega-}e^{-i2\omega t} $$, Thus, it can be expressed as:

Based on the current density formula $$ j_{a}=-e\int_{k}f(k)\{\partial_{a}\epsilon(k)-\varepsilon_{abc}\Omega_{b}eE_{c}(t) \} $$, it is noted that $$ \partial_{a}\epsilon(k)\partial_{bc}f_{0}(k) $$ is odd under time reversal within the approximation of a constant $$ \tau $$, leading to its vanishing upon integration. The second-order current corresponding currents are given by:

which represents the rectified current, and

which corresponds to the second harmonic current. Based on Eq.(1), the tensor of nonlinear Hall response is written as:

It is clear the $$ \chi_{abc} $$ is proportional to the dipole moment of the Berry curvature integrated over the occupied states, commonly referred to as the Berry curvature dipole^[21,54]:

In this vein, we can understand the requirement of the nonlinear Hall response induced by the Berry curvature dipole more clearly based on the analyses of the symmetry. Firstly, under T symmetry, both the group velocity and Berry curvature reverse their signs, but their product remains unchanged, indicating the nonlinear Hall response can be observed with T symmetry. Secondly, under P symmetry, the group velocity reverses its sign, but the Berry curvature does not, resulting in a zero Berry curvature dipole moment. Therefore, to observe the nonlinear Hall effect, the P symmetry must be broken.

Besides the symmetries mentioned above, other symmetries significantly influence the nonlinear Hall effect. The chiral symmetry plays a pivotal role in the nonlinear Hall effect^[55]. It refers to the absence of improper symmetries, such as inversion and mirror symmetries. The absence of these symmetries results in an inherent asymmetry, distinguishing between left- and right-handed configurations. The broken inversion symmetry, induced by chirality, ensures a finite valley-contrasting Berry curvature, which, in turn, gives rise to a Hall-like net transverse conductivity, contributing to the nonlinear Hall response^[56]. Moreover, when chiral symmetry is broken, the nonlinear Hall current can attain quantization^[57]. Beyond chiral symmetry, systems that break PT symmetry also manifest a third-order nonlinear Hall effect, driven by the Berry curvature quadrupole. PT symmetry enforces the vanishing of Berry curvature quadrupoles, so materials that break PT symmetry, such as bulk MnBi₂Te₄^[58] and FeSn^[59] under an external magnetic field, exhibit a third-order nonlinear Hall effect. The mirror symmetry and cyclic rotations symmetry also affect the nonlinear hall effect. Under $$ C_{n}^{z} $$ and $$ C_{3, 4, 6}^{z}T $$ symmetry, both the quantum metric and berry curvature dipole are forbidden. For the combined $$ C_{2}^{z}T $$ symmetry, the quantum metric dipole is allowed, but the Berry curvature dipole is forbidden. Conversely, $$ \sigma_{z}T $$ symmetry permits only the Berry curvature dipole^[48].

Side-jump and skew scattering

Besides the intrinsic mechanisms, disorder also plays an integral role in a variety of Hall effects, such as the extrinsic contributions of the anomalous, valley, and spin Hall effects^{[19,20,60,61]}. In the case of the nonlinear Hall effect, the intrinsic mechanism plays a crucial role, but disorder-related still cannot be overlooked. This is because this effect inherently requires the Fermi energy to intersect with the energy bands, making disorder scattering inevitable at the Fermi surface. In fact, disorder plays a role even at leading order, contributing critically to the overall response^[40,41].

Utilizing the Boltzmann equation:

where $$ W_{l'l} $$ is the average scattering rate from $$ l' $$ to $$ l $$, in conjunction with the 2D tilted massive Dirac model:

Du et al. systematically classified the contributions to the nonlinear Hall response under the influence of disorder. Their work identifies three key components: the intrinsic contribution, the extrinsic side-jump scattering, and the skew scattering mechanisms^[40].

The side-jump scattering occurs during the scattering of electrons off impurities or phonons in a material. When an electron scatters, its trajectory is deflected, not just by the usual scattering angle but also by an additional transverse displacement. The transverse displacement $$ \delta \textbf{r} $$ is proportional to the spin-orbit coupling strength and the gradient of the impurity potential^[62–64], so the accumulation of $$ \delta \textbf{r} $$ over multiple scattering events generates an effective transverse velocity contributing to the nonlinear Hall conductivity. The side-jump velocity induced nonlinear Hall response can be expressed as:

where $$ g_{l}^{b}=\tau_{l}\partial_{b}f_{l}^{(0)} $$. The side-jump also modifies the distribution function, which consequently gives rise to a second-order response:

On the other hand, skew scattering occurs when electrons are scattered asymmetrically due to spin-orbit interaction. The spin-orbit interaction causes the scattering to be asymmetric, meaning the probability of scattering to one side is different from the probability of scattering to the other side^[63,64]. Over many scattering events, the asymmetry leads to a net transverse current, which causes the nonlinear Hall effect^[65,66]. The skew scattering induced nonlinear Hall effect can also be separated into two parts:

and

where $$ w_{ll'}^{g} $$ and $$ w_{ll'}^{ng} $$ represent the Gaussian and non-Gaussian antisymmetric scattering rates, respectively.

In conclusion, the mechanisms governing the nonlinear Hall effect encompass the quantum metric dipole, the Berry curvature dipole, and disorder-induced phenomena such as side-jump and skew scattering. Both the quantum metric dipole and the Berry curvature dipole give rise to nonlinear Hall responses intrinsically linked to the quantum geometry of the system. Meanwhile, disorder-induced nonlinear Hall effects offer a valuable avenue for investigating disordered systems. These mechanisms manifest distinct experimental behaviors. Notably, the Berry curvature dipole exhibits a response that closely mirrors that of disorder-induced mechanisms, particularly due to its dependence on relaxation time. Importantly, the Berry curvature dipole is prohibited in systems exhibiting threefold rotational symmetry^[67]. Under such conditions, the nonlinear Hall effect is primarily driven by disorder and the quantum metric dipole, with the two contributions distinguishable by their contrasting relaxation-time dependencies.

Intrinsic symmetry broken in 2D materials

The nonlinear Hall response is generally measured through a Hall-bar device [Figure 1A]. To detect this effect, an alternating current $$ \mathit{\boldsymbol{I}}^{\omega} $$ with a low frequency $$ \omega $$ (typically between 10 and 1,000 Hz) is applied to the sample. The resulting transverse Hall voltage, which appears at twice of the applied frequency $$ 2\omega $$, is then measured using a lock-in technique^[22,23]. The low-frequency measurement in the nonlinear Hall effect provides a distinct advantage in separating the signal from other electronic noise, making it more feasible to study the nonlinear response in solid-state systems^[35].

The nonlinear Hall effect was initially observed in T_d-WTe₂, a 2D semimetal characterized by broken P symmetry^[22,23]. Through the typical measurement on a Hall-bar device, Kang et al. measured the double-frequency voltage of the few-layer WTe₂ at temperatures ranging from 2 to 100 K^[22]. They found the transverse electric field with $$ 2\omega\; (E_{\bot}^{2\omega}) $$ scales linearly on the square of the longitudinal electric field ($$ E_{\parallel} $$), as shown in Figure 3A. The slope decreases consistently with increasing temperature. The temperature dependence of the longitudinal conductivity $$ \sigma $$ was also measured [Figure 3B]. After a careful analysis, $$ \frac{E_{\bot}^{2\omega}}{(E_{\parallel})^{2}} $$ scales linearly with $$ \sigma^{2} $$ [Figure 3C]:

Figure 3. Experimental investigations of the nonlinear Hall response in WTe₂ and MnBi₂Te₄. (A) the $$ E_{\bot}^{2\omega} $$ depends linearly on the $$ (E_{\parallel})^{2} $$ at different temperatures. (B) The temperature dependence of $$ \sigma $$. (C) The nonlinear Hall signal as a function of the $$ \sigma^{2} $$. (D) The nonlinear longitudinal $$ V_{x}^{2\omega} $$ and transverse $$ V_{y}^{2\omega} $$ responses as a function of the input current. (E) The conductivity and carrier density of four septuple layers MnBi₂Te₄ at temperatures ranging from 2 to 30 K. (F) The nonlinear conductivity $$ \sigma_{yxx}^{2\omega} $$ ($$ \sigma_{xxx}^{2\omega} $$) as a function of the $$ \sigma_{xx}^{2} $$. (A-C) reprinted with permission^[22], 2019, CC BY license. (D-F) reprinted with permission^[26], 2023, CC BY license.

where $$ \xi $$ and $$ \eta $$ are constants. The anomalous Hall effect can result from Berry curvature, skew scattering, and side-jump mechanisms^{[16,19,78–80]}. Accordingly, the nonlinear Hall effect in few-layer WTe₂ is ascribed to contributions from both the Berry curvature dipole and scattering effects.

With further research into the nonlinear Hall effect, the mechanism of quantum metric dipole was proposed to induce the nonlinear Hall effect^[39]. This mechanism is referred to as the intrinsic nonlinear Hall effect since the $$ \tau $$ independence^[38]. The first observation of the intrinsic nonlinear Hall effect was in topological antiferromagnet MnBi₂Te₄^[26,27], whose spins couple ferromagnetically within each Te-Bi-Te-Mn-Te-Bi-Te septuple layer (SL) with an out-of-plane easy axis, while adjacent SLs couple antiparallel to each other^[81]. In the even layer MnBi₂Te₄, the P and T symmetries are violated but the PT symmetry remains intact. As shown in Figure 3D, the nonlinear Hall effect of the four SLs MnBi₂Te₄ is measured along both the transverse and longitudinal directions. Significant responses are observed in the two directions, aligning with predictions that the quantum metric dipole can drive both nonlinear Hall response and non-reciprocal transport phenomena^[82]. This is in stark contrast to the nonlinear Hall effect induced by the Berry curvature dipole, which only manifests the Hall response^[83]. To explore the underlying cause of the nonlinear response, the temperature dependence of the longitudinal conductivity $$ \sigma_{xx}^{\omega} $$ and charge carrier density n_e were measured. As shown in Figure 3E, the charge carrier density stays almost unchanged between 1.6 to 10 K, indicating that $$ \tau $$ is the predominant component to determine the conductivity in this range. Then the $$ \sigma_{yxx}^{2\omega} $$ and $$ \sigma_{xxx}^{2\omega} $$ as a function of the $$ (\sigma_{xx}^{\omega})^{2} $$ were plotted and fitted with

as shown in Figure 3F, they found the predominant contribution to both the $$ \sigma_{xxx}^{2\omega} $$ and the $$ \sigma_{yxx}^{2\omega} $$ is the quantum metric dipole ($$ \eta_{0} $$, $$ \tau $$-independence). This study introduces a technique for probing the quantum metric and offers a framework for designing magnetic nonlinear devices.

Given the multitude of mechanisms that can induce the nonlinear Hall effect, an effective approach to classify them is essential. In experiments, one can apply the scaling law proposed by Du et al.^[40]:

Here, the coefficients $$ C_{1, 2, 3, 4} $$ include the contributions from the Berry curvature dipole $$ (C^{in}) $$, side-jump $$ (C_{i}^{sj}) $$, intrinsic skew scattering $$ (C_{i}^{sk, 1}) $$, and extrinsic skew scattering $$ (C_{i}^{sk, 2}) $$ in the following forms:

In the limit $$ (T\rightarrow 0) $$, the scaling law simplifies to:

From the calculated values of $$ C_{1} $$ and $$ C_{2} $$, we can identify the dominant mechanism driving the nonlinear Hall effect. In the case of the Weyl semimetal TaIrTe₄^[25], it was found that $$ C_{1}=-1.6\times10^{-15} $$ and $$ C_{2}=2.6\times10^{-8} $$ m$$ ^{2} $$V$$ ^{-1} $$, indicating that the contribution from extrinsic skew scattering to the nonlinear Hall effect is smaller than that of the Berry curvature dipole and static disorder scattering.

In addition, based on Eq. (24), since $$ J=\sigma E $$, the second-order current can expressed as $$ J_{y}^{2\omega}=\sigma E_{y}^{2\omega} $$, and thus: $$ \frac{E_{yxx}^{2\omega}}{(E_{xxx}^{\omega})^2}=\frac{\sigma_{yxx}^{(2)}}{\sigma}=\xi\sigma^{2}+\eta $$. Given that $$ \sigma $$ is linearly dependent on the scattering time $$ \tau $$, the second-order conductivity $$ \sigma_{yxx}^{(2)} $$ scales as $$ \tau^{3} $$ and $$ \tau $$ with the coefficients $$ \xi $$ and $$ \eta $$, respectively. The $$ \tau^{3} $$ dependence contribution to the nonlinear Hall response originates from skew scattering, while the $$ \tau $$ dependence arises from the Berry curvature dipole and side-jump mechanisms. Through the scaling law, Lu et al. determined that the nonlinear Hall effect in BiTeBr is primarily attributed to skew scattering and side-jump mechanisms, as the Berry curvature dipole is prohibited by the material’s threefold rotational symmetry^[66]. The coefficient $$ \xi $$, which indicates the contribution from skew scattering, was calculated to be 6.9$$ \times $$10$$ ^{-15} $$ m$$ ^{3} $$V$$ ^{-1} $$S$$ ^{-2} $$ for the 4-nm sample. Furthermore, the sign of $$ \eta $$, which represents the contribution from side-jump, was found to change with increasing thickness. After a comparison between the skew scattering and side-jump contributions, it was concluded that the nonlinear Hall effect in BiTeBr is primarily dominated by skew scattering.

For the nonlinear Hall effect induced by the quantum metric dipole, a similar scaling analysis can be conducted. Based on Eq. (25), the contributions to the nonlinear Hall effect can be categorized into two distinct mechanisms: one that is independent of the scattering time $$ \tau $$, and the other one is dependent on $$ \tau $$. Since the quantum metric dipole is independent of $$ \tau $$, this distinction enables us to clearly differentiate the quantum metric dipole from other mechanisms.

Symmetry design through structure engineering

Due to the stringent symmetry requirements for the nonlinear Hall effect, the range of materials that can realize this effect is quite limited. Some of these materials require complex synthesis methods and may not even remain stable in air, which significantly restricts their practical applications^[22,24]. Additionally, the electronic properties of these materials are strongly affected by their crystal structure and composition, making it difficult to modify them as desired^[70,84], which reduces the ability to optimize the magnitude of the nonlinear Hall effect signals. Recently, some researchers have attempted to break the symmetry of materials through doping^[85]. However, this approach has inherent limitations. The doping concentration is constrained, and achieving a controllable distribution of the dopants is often challenging. Significant emphasis has been placed on the study of oxide interfaces, where spontaneous symmetry breaking inherently fulfills the conditions required for the nonlinear Hall effect^[86–88]. Likewise, there is growing emphasis on exploring heterostructures composed of 2D materials, where intentional symmetry breaking can be effectively achieved by stacking different materials^{[31,75,89,90]}. Recent years have witnessed significant progress in the design and fabrication of heterostructures, opening new avenues for this research. Utilizing techniques such as mechanical exfoliation and the dry-transfer method^[91,92], researchers can meticulously create 2D heterostructures tailored to specific experimental requirements. This innovative approach not only facilitates the investigation of fundamental physical phenomena but also paves the way for potential applications in next-generation devices, where engineered symmetry breaking may lead to novel functionalities.

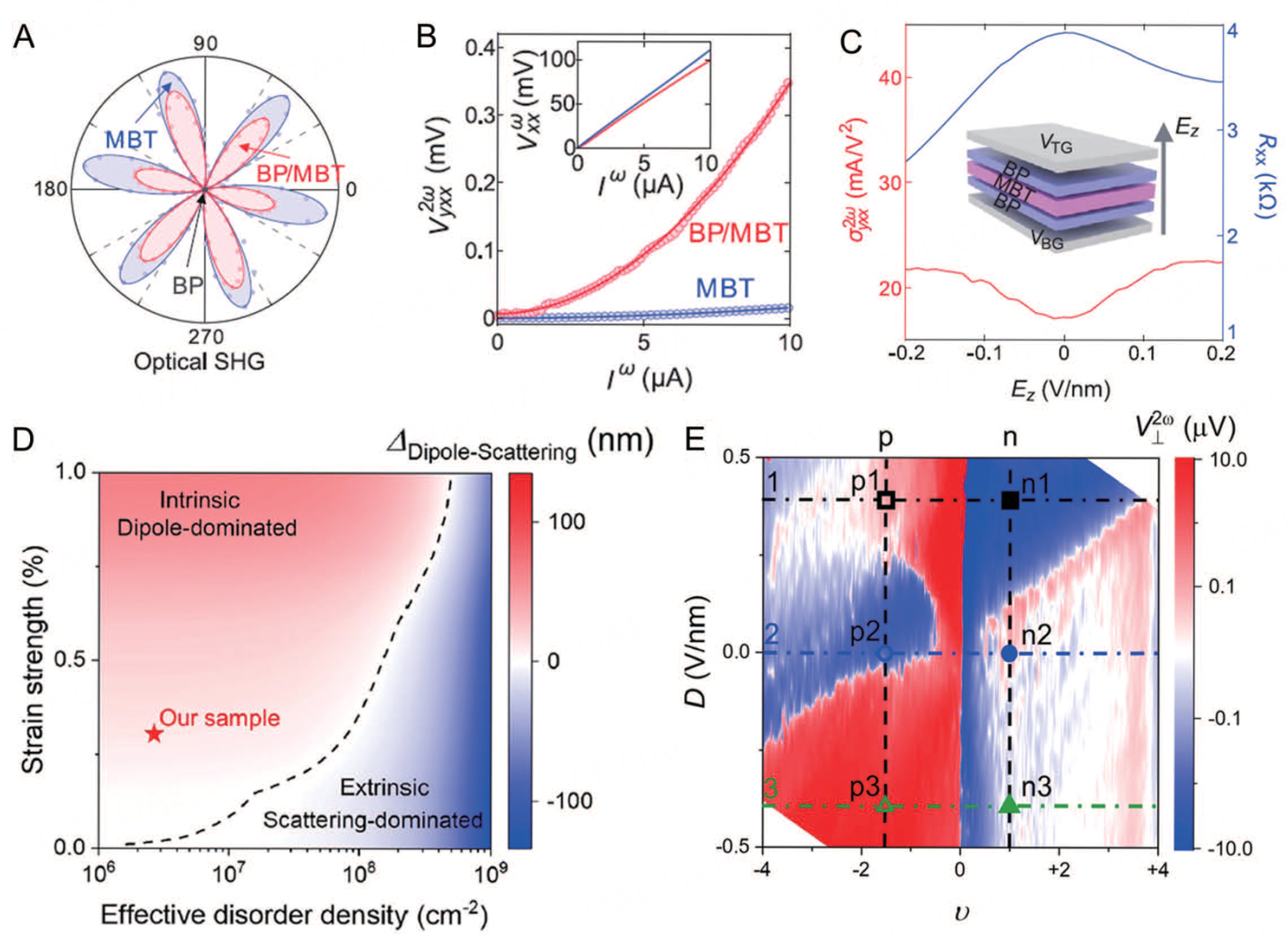
Through this structure engineering, Gao et al. investigated the nonlinear Hall effect in even layered MnBi₂Te₄ interfaced with black phosphorus (BP)^[27]. The lattice of MnBi₂Te₄ has $$ C_{3Z} $$ rotational symmetry. To break this symmetry, a BP layer is stacked onto the MnBi₂Te₄. As shown in Figure 4A, the polarization angle-dependent second harmonic generation (SHG) intensity of MnBi₂Te₄ exhibits six-fold rotational symmetry. In contrast, the SHG pattern of the BP/MnBi₂Te₄ heterostructure is asymmetric, indicating the BP breaks the $$ C_{3Z} $$ symmetry of MnBi₂Te₄. Figure 4B displays the nonlinear Hall signal of MnBi₂Te₄ before and after interfacing with BP. A prominent nonlinear Hall signal appears only after the introduction of BP, while the linear longitudinal voltage $$ V_{xx}^{\omega} $$ exhibits only a slight decrease (inset of Figure 4B), further confirming the nonlinear Hall signal is induced by symmetry breaking. Since the quantum metric dipole induced nonlinear Hall response does not require explicit PT symmetry breaking, applying a vertical $$ E_{Z} $$ field via dual gating to break PT symmetry has no impact on the nonlinear Hall signal. As shown in Figure 4C, the nonlinear Hall signal still remains at $$ E_{Z} $$ = 0, confirming this is a quantum metric dipole induced nonlinear Hall effect.

Figure 4. Experimental studies of the nonlinear Hall response in topological antiferromagnetic heterostructure (BP/MnBi₂Te₄) and twisted bilayer graphene. (A) Optical second harmonic generation measurements of a 6 SLs MnBi₂Te₄ before and after being coupled with BP. (B) The $$ V_{yxx}^{2\omega} $$ and $$ V_{xx}^{\omega} $$ before and after being coupled with BP. (C) The $$ E_{Z} $$ dependence of the $$ \sigma_{yxx}^{2\omega} $$ and $$ R_{xx} $$. (D) Phase diagram of the nonlinear Hall effect. The dominated mechanism changes with strain strength and effective disorder density, with red (blue) regions indicating dipole (scattering) dominance. (E) The $$ V_{\bot}^{2\omega} $$ varies with $$ \upsilon $$ and D. (A-C) reprinted with permission^[27], Copyright 2023, The American Association for the Advancement of Science. (D and E) reprinted with permission^[93], Copyright 2023, The American Physical Society.

With the advancement of 2D van der Waals stacking technology, the fabrication of 2D moiré superlattices has become feasible through techniques such as tear-and-stack^[94] and cut-and-stack^[95] methods. Researchers have successfully synthesized 2D moiré superlattices in materials including twisted trilayer graphene^[95–97], twisted bilayer boron nitride (tBN), and twisted WSe₂-MoSe₂ heterobilayers^[98]. These structures exhibit intriguing physical properties, including superconductivity^[97,99,100], topological phases^[76,101] and correlated insulating states^[102–104]. Furthermore, the spontaneous atomic reconstruction associated with these moiré patterns leads to symmetry breaking within the material, thereby facilitating the emergence of the nonlinear Hall effect.

Recently, Huang et al. detected a nonlinear Hall signal in high-mobility monolayer twisted graphene samples^[93]. Two mechanisms for generating the nonlinear Hall effect in graphene superlattices have been proposed. As shown in Figure 4D, the Berry curvature dipole dominates in samples with high strain and low impurity concentration, whereas disorder dominates in samples with low strain and high impurity concentration. Additionally, the Berry curvature dipole can be effectively tuned by gate voltage, even allowing a change in the direction of the dipole [Figure 4E]. This study presents an efficient method to control and manipulate the amplitude and direction of the Berry curvature dipole, thereby enabling control over the nonlinear Hall response.

In addition to the 2D materials previously mentioned, the nonlinear Hall effect has been identified in a variety of other materials in recent years [Table 2]. The Weyl semimetals, such as MoTe₂^[105] and TaIrTe₄^[25], with a $$ T_{d} $$ structure, exhibit mirror plane breaking on their surfaces, giving rise to the nonlinear Hall effect. Elemental materials such as Te^[65,107] and Bi^[108], along with topological insulators such as Bi₂Se₃^[49], distinguished by their unique surface states, can also significantly contribute to the generation of nonlinear signals. Similarly, Rashba materials, such as BiTeBr^[66], which exhibit significant Rashba-type band splitting, can generate a nonlinear Hall response. Furthermore, the spin-valley-locked Dirac material BaMnSb₂^[106], with its non-centrosymmetric orthorhombic structure, serves as an exemplary platform for facilitating the nonlinear Hall effect. Additionally, advanced structural engineering approaches, including heterostructures^[27,49] and 2D moiré superlattices^{[83,111–113]} designed to break inversion symmetry, offer a compelling route for the realization of this intriguing phenomenon.

Other nonlinear transport effects

The nonlinear Hall effect typically involves a quadratic response of the longitudinal Hall voltage to the applied transverse current. However, in some materials, there could be higher-order responses in Hall effect. The second-order derivatives of the Berry connection polarizability could also induce the third-order nonlinear Hall effect. Analogous to the second-order nonlinear Hall effect, the third order nonlinear conductance can be expressed as^[58]:

Distinct from the linear and second-order nonlinear Hall effects, the third-order Hall effect follows unique symmetry constraints and does not require broken T or P symmetry, making it a valuable tool for characterizing materials that preserve both symmetries^[114].

The first observation of the third-order nonlinear Hall effect was made in MoTe₂^[115]. As depicted in Figure 5A, in the $$ T_{d} $$ phase of MoTe₂, symmetry broken arises from the material's surface. With increasing thickness, the third-order nonlinear Hall effect becomes increasingly distinct, as illustrated in Figure 5B. Furthermore, Wang et al. reported a pronounced third-order nonlinear Hall effect at room temperature^[116], as shown in Figure 5C. Additionally, the third-order nonlinear Hall effect has been observed in magnetic systems. Li et al. identified a third-order response in MnBi₂Te₄^[58]. Notably, Figure 5D and E reveals that the measured $$ V^{3\omega}_{xx} $$ exhibits an even dependence on the magnetic field, whereas $$ V^{3\omega}_{xy} $$ displays an odd dependence. The field dependence of these responses suggests that the longitudinal third-order response is driven by the Berry connection polarizability, while the transverse response is governed by the Berry curvature quadrupole. Similarly, the quantum Hall effect also manifests a third-order response. He et al. observed the third-order nonlinear Hall effect in graphene within quantum Hall phases^[117]. Figure 5F illustrates that the third-order Hall response is independent of temperature. The extrinsic effects, including skew and side-jump scattering of electrons, which are dependent on scattering time, are supposed to be suppressed in quantum Hall states. As a result, the nonlinear Hall response observed in quantum states provides an ideal platform for exploring the intrinsic nonlinear Hall effect. In addition to the materials discussed above, the third-order nonlinear Hall effect has also been observed in Weyl semimetals WTe₂^[114], in transition metal dichalcogenides VSe₂^[118], which is characterized by charge density wave modulation, and in the misfit layer compound (SnS)_1.17(NbS₂)₃^[119], which exhibits a giant third-order response.

Figure 5. The third-order nonlinear Hall effect in several materials. (A) b-c plane of few-layer $$ T_{d} $$ MoTe₂. (B) The $$ V_{\bot}^{n\omega} $$ of MoTe₂ as a function of $$ V_{\parallel} $$, with red demoting the third-order response and black representing the second-order response. (C) The $$ V_{\bot}^{3\omega} $$ in TaIrTe₄ as a function of $$ V_{\parallel} $$. (D and E) The $$ V_{xy}^{3\omega} $$ and $$ V_{xx}^{3\omega} $$ of MnBi₂Te₄ as functions of magnetic field at different temperatures. (F) The $$ V_{y}^{3\omega} $$ of graphene under quantum Hall states as a function of $$ V_{g} $$ at varying temperatures. (A and B) reprinted with permission^[115], 2021, CC BY license. (C) reprinted with permission^[116], 2022, CC BY license. (D and E) reprinted with permission^[58], 2024, CC BY license. Panel F reprinted with permission^[117], 2024, CC BY license.

In addition to the higher order nonlinear Hall effect, the nonlinear spin Hall response can be realized through charge-to-spin conversion^[120,121]. In thermally driven systems, the nonlinear response includes effects such as the nonlinear Nernst effect, the nonlinear Seebeck effect, and the nonlinear anomalous thermal Hall effect^[122–125]. The planar Hall effect, unlike the traditional Hall effect, occurs when the Hall voltage, electric field, and magnetic field are coplanar^[126–128]. The nonlinear planar Hall effect further introduces a higher-order response, where the transverse voltage scales nonlinearly with the applied current or magnetic field^[93,129,130]. Collectively, these nonlinear transport phenomena offer rich opportunities for exploring new physics and developing innovative applications in science and technology.

Device applications

Due to its unique sensitivity to symmetry breaking and material properties, the nonlinear Hall effect offers applications in phase probing and the investigation of topological phenomena in condensed matter systems^[131,132]. In twisted double bilayer graphene, the application of a perpendicular electric field can concurrently adjust both the valley Chern number and the Berry curvature dipole, offering a tunable platform to investigate topological transitions^[113], as shown in Figure 6A-C. The Berry curvature dipole can also be tuned by strain^[110,133] [Figure 6D]. This provides new ideas and methods for designing piezoelectric-like devices, such as strain sensors.

Figure 6. Device applications of the nonlinear Hall effect span diverse fields, including probing topological transitions, developing strain sensors, and creating wireless radiofrequency rectifiers. (A) Schematic of the nonlinear Hall measurement. (B) Band structures of the K valley for two different interlayer potential values, with the overlaid color representing the Berry curvature of the corresponding flat bands. (C) The variation in the Berry curvature dipole as a function of energy E at two different Fermi energies. (D) A strain sensor leveraging the nonlinear Hall response. (E) Wireless radiofrequency rectifier via the nonlinear Hall response. (A-C) reprinted with permission^[113], 2022, CC BY license. (D) reprinted with permission^[133], Copyright 2020, The American Physical Society. Panel E reprinted with permission^[65], 2024, CC BY license.

Beyond its scientific significance in probing quantum geometry and crystalline symmetry, the nonlinear Hall effect holds substantial potential for practical applications, particularly in energy harvesting and rectifying devices^[25,47,134], as shown in Figure 6E. Materials exhibiting the nonlinear Hall effect can function as wireless radiofrequency (RF) rectifiers operating without an external bias (battery-free), and in the absence of a magnetic field by utilizing a driving alternating current in place of an oscillating electromagnetic field^[135]. For example, the use of materials such as TaIrTe₄^[25] and MnBi₂Te₄^[27] in RF rectification has demonstrated cutoff frequencies reaching up to 5 GHz, which is sufficient to encompass the widely utilized 2.4 GHz Wi-Fi channel. Furthermore, BiTeBr-based rectifiers have exhibited RF rectification initiating at power levels as low as -15 dBm (0.03 mW), aligning closely with ambient RF power levels ranging from -20 to -10 dBm^[66,136]. In addition, the rectified output in tellurium thin flakes can be significantly enhanced through the application of a gate voltage^[65]. This class of Hall rectifiers, relying on the intrinsic material properties, effectively bypasses the limitations imposed by transition time and thermal voltage thresholds, presenting a promising solution for efficient, low-power energy conversion technologies^[137].

Authors’ contributions

Made substantial contributions to conception and design of the study: Niu, W.; Fang, Y. W.

Writing: Wang, S.; Niu, W.; Fang, Y. W.

Availability of data and materials

Not applicable.

Financial support and sponsorship

The work carried out by Wang, S. and Niu, W. was supported by the Natural Science Foundation of Nanjing University of Posts and Telecommunications (NY222170).

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

© The Author(s) 2025.