Hot deformation behavior investigation of heat-resistant aluminum matrix composite based on Arrhenius model and machine learning

Material preparation

Pure aluminum powder (Shanpu Chemical Co., Ltd., Shanghai, China) with an average particle size of 10 μm was used as the starting material to prepare the composite. The aluminum powder was ball-milled using planetary ball milling (ND8-4L, Nanjing Nanda Tianzun Electronics Co., Ltd., China) with 1-liter stainless steel vials and 1 kg of stainless steel balls as the milling media. Milling took place in an argon environment. The process was carried out at a speed of 210 rpm over a duration of 30 h, with a 15:1 ball-to-powder mass ratio set. Moreover, 10 wt.% ethanol was added into the aluminum powder as the process control agent. The milled powder was sealed into the graphite die inside the glove box and then consolidated at 893 K and 50 MPa for 30 min in a vacuum hot-pressing sintering furnace (CXZG-15, Ningbo Chenxin Weike Industrial Technology Co., Ltd., China). The material cooled in the furnace after sintering at a rate of approximately 15 K/min.

Microstructure characterization

Microstructures of the obtained composite were characterized using field emission scanning electron microscopy (SEM, Sigma500, ZEISS, Germany) with electron backscatter diffraction (EBSD, Octane Elite Ultra, EDAX, USA) and transmission electron microscopy (TEM, JEM-2100F, JEOL, Japan). The phase of the nanocomposite was analyzed by an energy dispersive spectrometer (EDS, OXFORD, X-Max80, UK) and X-ray diffraction (XRD, PANalytical, Empyrean, Netherlands).

Figure 1A illustrates the SEM images of representative composites. The images reveal a significant presence of nanostrips evenly distributed within the matrix. The nanostrips have a width of about 10 nm, and their average length is about 180 nm. The volume fraction of these nanostrips is estimated as 12% from the SEM images by ImageJ software. Figure 1B displays EBSD images of the composite, indicating that the grains of the aluminum matrix exist at the nanoscale. Figure 1C shows that the material mainly contains Al, with a small amount of Al₄C₃. Figure 1D indicates that the nanostructures in the matrix primarily contain O, and the quantitative analysis of the energy spectrum surface scan also shows that the content of O is greater than that of C. Therefore, we preliminarily conclude that most of our nanostrips are Al–O structures. The absence of characteristic peaks for Al–O nanostrips in the XRD results may be attributed to the extremely small size of the nanostrips. Further detailed structural characterization will be presented in future work.

Figure 1. (A) Typical SEM image of composite; (B) Typical EBSD image of composite; (C) Typical XRD image of composite; (D) Typical EDS image of composite. SEM: Scanning electron microscopy; EBSD: electron backscatter diffraction; XRD: X-ray diffraction; EDS: energy dispersive spectrometer.

The formation of Al₄C₃ is likely due to the reaction of carbon introduced during processing with Al at elevated temperatures. The high content of Al–O nanostructures may result from the reaction between anhydrous ethanol and the aluminum matrix during ball milling and hot pressing, despite the use of inert atmospheric conditions.

Compression test

Compression tests were conducted at strain rates of 0.001, 0.01, and 0.1 s^-1, and at temperatures of 473, 523, 573, 623, and 673 K. Each condition was tested three times using a testing machine (MTS, Instron 2367 equipped with a heating furnace, Instron, USA), with cylindrical specimens measuring 4 mm in height and 2 mm in diameter. All test specimens were prepared using a wire-cut electrical discharge machining (WEDM, Jiangsu Founder CNC Machine Tool Co., Ltd, DK7735, China), ensuring geometric accuracy within ± 0.01 mm. The specimens were gradually heated to the specified temperature, increasing at a rate of 10 °C per minute and held for 10 min to ensure uniform thermal conditions. Stress-strain curves were then derived from the force-displacement data.

Arrhenius model

The hot deformation behavior of composites is governed by thermally activated processes, which can typically be described using the Arrhenius-type equation^[22]. This equation relates flow stress, strain rate, and deformation temperature during the hot deformation process. It is particularly useful for understanding how the material responds under different thermal and mechanical conditions.

For different stress levels, the Arrhenius model can be adapted as follows. When the material is under low stress, the flow stress and strain rate follow a power-law relationship:

For higher stress levels, the model is adjusted to reflect the impact of stress on material’s flow behavior, which is usually expressed as:

Finally, to account for all stress levels, the model can be generalized using

which incorporates hyperbolic sine function to describe strain rate’s dependence on flow stress. A and A₁ are structural factors, $$ \dot{\varepsilon} $$ is the strain rate, σ denotes flow stress, Q is the hot deformation’s activation energy, R is the molar gas constant valued at 8.31 J/(mol·K), and T is the deformation temperature measured in Kelvin. The parameter α is a stress level parameter, β is a constant independent of deformation temperature, and n and n1 are stress exponents. The relationship between α and β satisfies the relation n1 = β/α^[22].

Additionally, Zener and Hollomon^[35] showed that the flow stress is affected by temperature and strain rate, which can be effectively described using a temperature-compensated strain rate factor. This parameter, known as the Zener-Hollomon parameter (Z), can be incorporated into the Arrhenius equation as follows:

The Z parameter is particularly useful for characterizing deformation processes because it allows for the comparison of deformation conditions at different temperatures and strain rates.

Database establishment of neural network

To ensure both diversity and reliability of the dataset, a wide range of testing conditions was considered as the input features, including:
(1) Temperature: The testing temperature of the sample, expressed in degrees Fahrenheit (K).
(2) Strain Rate: The rate at which strain is applied, expressed in inverse seconds (s^-1).
(3) Strain: A measure of the amount of deformation, typically expressed as a percentage without units.

The output target is the flow stress (τ), measured in megapascals (MPa), which indicates the material’s resistance to deformation under specific conditions. The flow stress is derived from the experimental stress-strain curves and is crucial for analyzing material performance and determining optimal processing parameters. It is important to note that these input features and output targets are consistent across all subsequent models in this study.

These conditions were carefully selected to capture the hot deformation behavior of the composite comprehensively. The temperature range was from 473 to 673 K, the strain rates were set at 0.001, 0.01, and 0.1 s^-1, and the strain ranged from 0.05 to 0.2. A total of 1,500 datasets were collected from the experimental flow stress-strain curves, consisting of 100 strain values, three strain rates, and five temperatures.

To enhance model convergence and training efficiency, the raw data is normalized prior to the training process, ensuring that it falls within the range of 0 to 1, as determined by:

where X_i represents the original data, X_min indicates the minimum value of the dataset, and X_max signifies the maximum value of the dataset. Normalization reduces the influence of varying magnitudes of input variables, ensuring that all features contribute equally during training.

The normalized dataset was split into two segments: 80% was allocated for training the neural network, and the remaining 20% was used as a test set to assess the network’s performance.

To quantify predictive accuracy, the mean absolute error (MAE), the root mean square error (RMSE), and the coefficient of determination (R²) were introduced to assess the models’ performance. These metrics provide complementary understanding of the model’s effectiveness, with R² reflecting proportion of variance explained, RMSE quantifying the average deviation magnitude, and MAE capturing the absolute prediction error. These metrics are given below:

Here n represents the sample’s number, y_i stands for the i-th samples’ true value, $$ \bar{y} $$ is the mean value of the true samples, and x_i denotes the i-th sample’s predicted value. A higher R² value and lower RMSE and MAE values demonstrate superior model effectiveness. These metrics offer a comprehensive assessment of the model’s ability to predict outcomes under various conditions.

BPNN

The BPNN functions in two key phases: forward and backward propagation. In the forward phase, input data is processed through layers to produce output signals. When the output deviates from the target, the network initiates back-propagation, redistributing the error to adjust weights and thresholds. This continuous adaptation improves the network’s accuracy in predicting flow stress^[25].

The BPNN architecture used in this study includes an input layer, an output layer, and a hidden layer composed of several interconnected neurons, as illustrated in Figure 2. The input layer comprises three nodes representing temperature, strain rate, and strain. The hidden layer includes 15 neurons, which were selected based on empirical testing to balance model complexity and accuracy. The activation function selected for the hidden layer is the hyperbolic tangent sigmoid function, whereas the output layer utilizes a linear transfer function. The parameters for the BPNN include a maximum iteration count of 100, a target error of 0.0001, a learning rate of 0.5, and 15 neurons in the hidden layer. These parameters were chosen based on preliminary experiments to ensure stable convergence and high accuracy. After establishing the model, a set of independent data is input for predicting the flow stress.

Figure 2. Model based on BPNN. BPNN: Back-propagation neural network.

GA

In a BPNN, the weight parameters and activation functions are critical factors influencing performance. The output produced by any individual neuron can be determined using

where n represents the number of input nodes, x_i stands for the input vector, g refers to the activation function, w_i denotes the weight vector, b_i indicates the bias, and y signifies the output. For each computation, the error signal, representing the difference between experimental and predicted values, is propagated backward to modify the weights. If the initial weights and thresholds are poorly chosen, the training process may become stuck in local minima, preventing the model from reaching the global minimum of the error function. To enhance the accuracy of the model, this study employs a GA to optimize the BPNN.

The GA begins with a population of individuals, each representing a potential solution to an optimization problem. Each individual is a chromosome containing genes that determine its phenotype. The algorithm evolves the population through generations based on natural selection principles, yielding increasingly effective solutions.

Individuals are selected according to their fitness, and genetic operations such as crossover and mutation create a new population with innovative solutions. This iterative process enhances adaptation, resulting in the best individual of the final generation representing a near-optimal solution to the problem. Based on this approach, a more stable GA-BPNN model has been established, with the structure illustrated in Figure 3. The configuration of the BPNN model is consistent with the previous discussion. After adjustments, the final parameters for the GA are as follows: 2,000 training epochs, learning rate of 0.01, momentum factor of 0.01, target training error of 0.0001, population size of 30, number of evolution iterations of 50, and mutation and crossover probabilities of 0.2 and 0.8. After establishing the model, a set of independent data was input to describe the flow stress.

Figure 3. Schematic diagram of the GA-BPNN model structure. GA-BPNN: Genetic algorithm-optimized back-propagation neural network.

The hot processing map

The ability of the composite for plastic deformation and its assistance in identifying regions of flow instability can be reflected by the hot processing map. It serves as a vital research tool in the field of plastic forming. A widely utilized approach for constructing such a map is the dynamic materials model (DMM) proposed by Prasad et al.^[36]. It integrates power dissipation map with instability map to identify the optimal parameter window for hot processing of composites. The input energy P of the system can be split into two parts: the dissipative quantity and the cooperative dissipative quantity:

Here, G is the energy dissipated as heat during plastic deformation. This energy arises from irreversible processes such as dislocation motion and lattice friction and contributes little to microstructural evolution. The symbol J represents the energy expended in altering the microstructure during the deformation process, such as DRX, grain boundary migration, and dislocation annihilation. This component is critical for understanding microstructural changes under specific processing conditions.

The distribution between G and J is governed by m (strain rate sensitivity index), defined as:

Under standard conditions, m’s value exhibits a nonlinear relationship with strain rate and temperature. In the case of viscoplastic solids, m’s value ranges between 0 and 1. As the m value increases, microstructural dissipation also increases. When m approaches zero, the energy dissipation is primarily dominated by G, with minimal contribution from J. This condition is often observed in scenarios involving dislocation pile-up and shear localization, which can limit the extent of microstructural evolution. Conversely, when m approaches one, the energy dissipation shifts towards J, potentially promoting DRX and a more uniform grain structure. These mechanisms are associated with improved material stability and deformation homogeneity.

Assuming that the material follows the constitutive equation:

The cooperative dissipative quantity J can be derived as:

When m = 1, the dissipation co-energy J attains its peak value.

The dissipation efficiency factor η, defined as:

provides a dimensionless measure of how effectively the energy is utilized for microstructural evolution. The dimensionless parameter η generally reflects the deformation mechanisms exhibited by materials under particular conditions of temperature and strain rate. High η values often correspond to regions of DRX, while low η values tend to indicate shear localization or other instability mechanisms. A power dissipation diagram can be developed by illustrating how the parameter η changes with strain rate and temperature.

Prasad et al. introduced an instability criterion derived from the principle of maximum irreversible thermodynamics, specifically for extensive plastic flow in continuous media^[37]. The instability occurs when:

Here, D represents the dissipation function, which characterizes the material’s constitutive behavior and is derived from the dissipated power. According to the principle of the DMM, the cooperative dissipation quantity J can substitute the dissipation function D. Thus, the instability criterion becomes:

Then, we can obtain

According to the cooperative dissipative quantity J expressed in Equation (14), we obtain

From Equations (18) and (19), we can introduce an instability parameter ξ($$ \dot{\varepsilon} $$):

When ξ($$ \dot{\varepsilon} $$) < 0, the material is prone to instability, often associated with microstructural phenomena such as shear banding, dislocation pile-up, or crack initiation.

By plotting the ξ values on the two-dimensional plane of T vs. ln$$ \dot{\varepsilon} $$, the instability map can be derived. When overlaid with the power dissipation map (η), hot processing map provides critical guidance for optimizing the processing parameters of composites. DRX zones can be identified as regions with high η and positive ξ, enabling precise control over grain size and texture. Conversely, failure-prone zones with low η and negative ξ can be avoided to enhance material performance during processing. By correlating the map with experimental microstructural observations, this methodology bridges the gap between theoretical modeling and practical applications in plastic forming.

Flow behavior

Figure 4 illustrates the true stress vs. true strain curves for the composite material under different temperatures and loading rates. Under quasi-static loading conditions, the composite exhibits a strength of up to 400 MPa at 473 K. When the temperature rises to 673 K, strength remains approximately 200 MPa. Figure 5 depicts the correlation between temperature and peak stress, indicating that peak stress decreases as the deformation temperature increases, while it increases with higher strain rates.

Figure 4. Curves of true stress vs. true strain under various strain rates and temperatures during compression: (A) strain rate of 10^-1; (B) strain rate of 10^-2; (C) strain rate of 10^-3.

Figure 5. The correlation between temperature and peak stress.

In Figure 4, the stress exhibits a rapid increase shortly after loading commences, which can be attributed to the abrupt rise in dislocation density induced by external forces, leading to a phenomenon known as work hardening. After the maximum flow stress is achieved, the stress-strain curve gradually declines and eventually stabilizes. This decline is attributed to the diminishing strengthening effect of the nanostrips. At higher temperatures, mechanisms of softening, including DRX and DRV, interact with hardening processes such as strain hardening. Once peak stress is reached, the softening mechanisms prevail, resulting in a gradual reduction in the stress-strain curve. Ultimately, the interaction between the softening and hardening mechanisms nearly balances out, leading to a stable stress-strain response^[38]. As shown in Figure 5, an analysis comparing peak stress values at various strain rates demonstrates that the composite shows sensitivity to strain rate changes. Specifically, at a constant deformation temperature, an increase in strain rate corresponds to an increase in peak stress. This phenomenon occurs because higher strain rates accelerate dislocation movement, resulting in the production of relatively large deformations over shorter time intervals, which in turn leads to significant dislocation pile-up. The substantial increase in dislocation density raises the critical shear stress during deformation^[39]. Additionally, the increased strain rate results in a shorter deformation time, hindering DRV and DRX^[40,41]. This rapid deformation not only accelerates dislocation movement but also increases the likelihood of localized stress concentrations around the reinforcing phases. As the strain rate rises, the matrix experiences rapid plastic deformation, while the reinforcing phases may not deform at the same rate due to their different mechanical properties. This discrepancy creates a situation where the reinforcing phases can act as stress concentrators, exacerbating the non-uniform distribution of stress within the matrix^[42-44]. The presence of these stress concentrations can lead to localized yielding in the matrix, which further complicates the overall deformation behavior. Consequently, the matrix’s ability to undergo plastic deformation is significantly impeded by the presence of the reinforcing phases.

In contrast, maintaining a constant strain rate while raising the temperature results in a reduction in peak stress. This reduction is attributed to enhanced thermal motion of atoms at higher temperatures, which increases dislocation mobility and weakens the work hardening and dislocation pile-up within the matrix. Several strengthening mechanisms are also diminished at elevated temperatures, such as the reduced effectiveness of grain refinement due to grain growth and the decreased interfacial bonding strength between the reinforcing phases and the matrix. This reduction in bonding strength results in a diminished capacity of the matrix to transfer loads to the particles, significantly lowering the shear resistance encountered by the particles. Furthermore, the rise in temperature can intensify the DRV and DRX processes within the matrix, ultimately resulting in a decrease in flow stress.

It is worth noting that at a loading rate of 10^-3 s^-1, we observed a significant decrease in the experimental curves (black and red lines) in the final sections at temperatures of 473 and 523 K. This corresponds to the material failure stage (e.g., crack propagation, interfacial peeling, or local necking), which occurs outside of the steady-state deformation state. The work in this paper is mainly focused on describing the steady-state flow behavior, so all subsequent models do not take into account the failure stage. We selected a strain range of 0.05 to 0.2. This choice ensures that our analysis focuses on the steady-state flow behavior and is not influenced by the failure stage.

Arrhenius model

In this chapter, we will derive the Arrhenius equation to elucidate the relationship between strain rate stress and temperature. Taking the logarithm of Equations (1)-(4) results in

By substituting the peak stress at a strain of 0.1 and the corresponding strain rate into Equations (21) and (22), and applying linear regression using the least squares method, we obtain the linear relationships between ln$$ \dot{\varepsilon} $$ and lnσ, as well as σ under different deformation conditions, as shown in Figure 6. From Equations (21) and (22), it can be observed that n1 and β represent the slopes of the lines in Figure 6A and B, respectively. Thus, the average values of n1 and β are 2.08 × 10^-2 and 6.34. Additionally, α = n1/β; the calculated value of α is 3.28 × 10^-3.

Figure 6. (A) The correlation between ln$$ \dot{\varepsilon} $$ and lnσ; (B) The correlation between ln$$ \dot{\varepsilon} $$ and σ.

At a fixed strain rate, taking the partial derivative of Equation (23) with respect to (1/T) and rearranging gives activation energy’s expression:

The linear relationships between ln[sinh(ασ)] and (1/T) as well as ln[sinh(ασ)] and ln$$ \dot{\varepsilon} $$ are shown in Figure 7. The curves’ average slopes in Figure 7A and B were calculated, and the product of these slopes was used to determine the composite’s activation energy, which was found to be 269.93 kJ/mol.

Figure 7. (A) The correlation between ln[sinh(ασ)] and (1/T); (B) The correlation between ln[sinh(ασ)] and ln$$ \dot{\varepsilon} $$.

The parameter Z reflects the relationship between the strain rate and activation energy, as given in Equation (24). By graphing ln(Z) vs. ln[sinh(ασ)], the accuracy of the analysis can be validated, as depicted in Figure 8. Furthermore, the intercept yields the value of ln(A). Thus, we can obtain the value of A as 1.67 × 10²⁰. The value of n = 23.1 can be determined from the curve’s slope. The correlation of correlation R² for lnZ and ln[sinh(ασ)] exceeds 0.95.

Figure 8. The correlation between ln(Z) and ln[sinh(ασ)].

Finally, the derived constitutive equation for hot deformation, encompassing all conditions, is expressed as:

where A = 1.67 × 10²⁰, α = 3.28 × 10^-3, n = 23.1, R = 8.31 J/(mol·K), and Q = 269.93 kJ/mol.

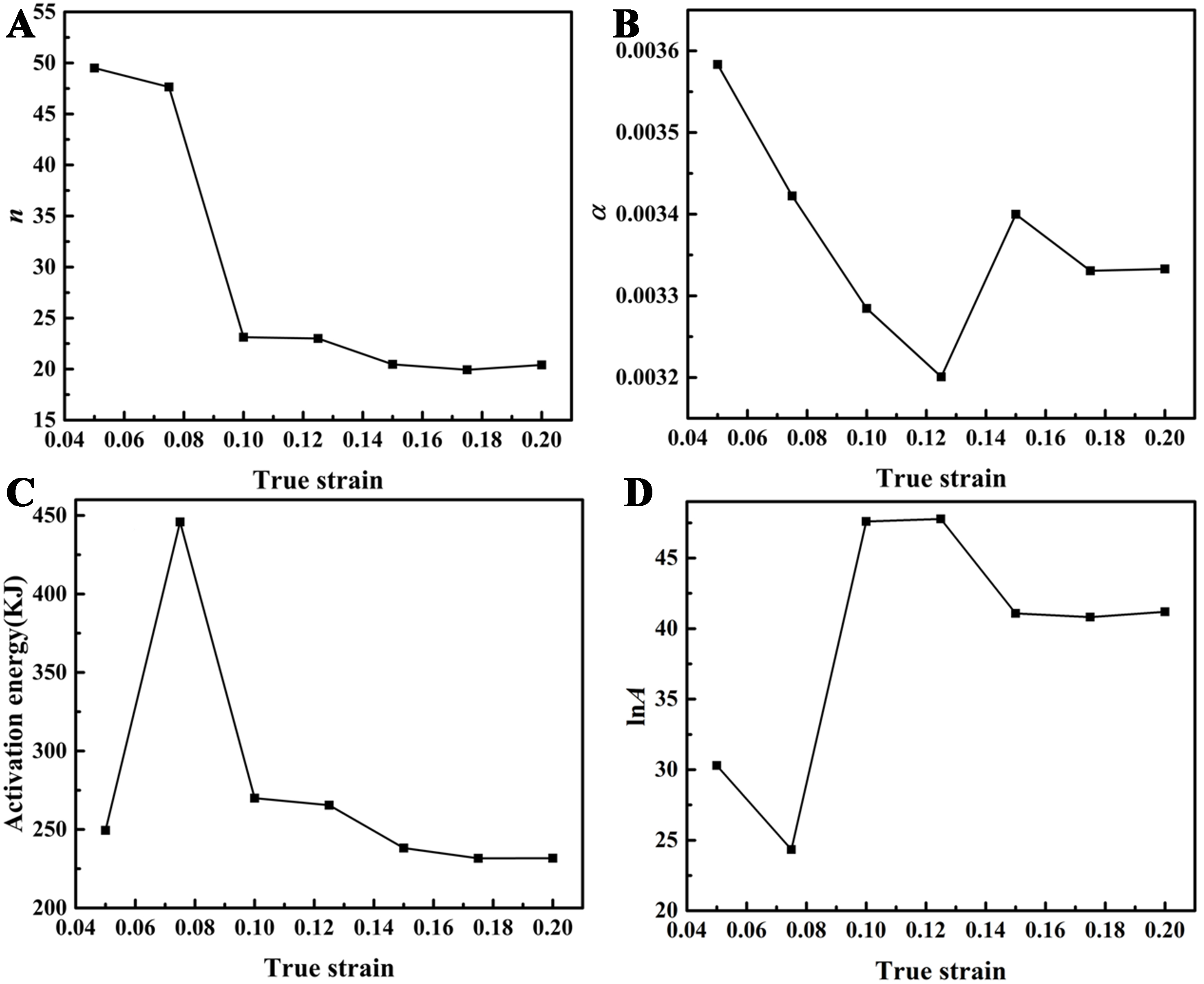
Although the Arrhenius model successfully derives the constitutive equation, it overlooks the equally important strain parameters. The activation energy for deformation and the constants are greatly affected by strain. Consequently, integrating strain parameters into the Arrhenius equation is crucial. In the strain range of 0.05 to 0.2, values are sampled at intervals of 0.025, and the material constants in Equation (29) are calculated for each corresponding strain value. The variation of constants with strain is depicted in Figure 9. Additionally, we represent the constants α, n, Q, and lnA at different strains using a fifth-degree polynomial, as given in

Figure 9. The relationship between material constants and true strain.

Then, we determine the coefficients of these equations through fitting, with the coefficients’ values presented in Table 1.

After calculating the material constants, the established strain-compensated constitutive equation can yield flow stress values at different strains. By calculating values within a strain range of 0.05 to 0.2 at intervals of 0.025, both experimental and model-derived flow stress values were compared. Figure 10 illustrates the comparison between experimental data and model-derived values. The model-derived values closely align with the experimental findings obtained at strain rates of 10^-3. At high strain rates, the material’s response becomes more complex due to rapid deformation processes. The strain-compensated Arrhenius model may not fully capture the interplay between work hardening and softening mechanisms (such as DRV and recrystallization) that dominate at these rates.

Figure 10. Flow stress experimental values and model-derived values at different strain rates based on the strain-compensated Arrhenius equation: (A) 10^-1; (B) 10^-2; (C) 10^-3.

ANN model

BPNN model

The BPNN model was utilized to describe the flow stress during the hot deformation process. By calculating flow stress values within a strain range of 0.05 to 0.2 at intervals of 0.025, the experimental and model-derived values were compared. The outcomes, as illustrated in Figure 11, demonstrate that the BPNN produces accurate flow stress values across different conditions, including temperature, strain rate, strain, and other processing parameters.

Figure 11. Model-derived flow stress values generated from the BPNN model with experimental values at different strain rates: (A) 10^-1; (B) 10^-2; (C) 10^-3. BPNN: Back-propagation neural network.

GA-BPNN model

The flow stress was characterized using the GA-BPNN model. By calculating values of flow stress within a strain range of 0.05 to 0.2 at intervals of 0.025, the experimental and model-derived values were compared. The results are presented in Figure 12, where it is evident that the difference between values derived from the GA-BPNN model and those obtained experimentally is minimal.

Figure 12. Comparison of model-derived flow stress values obtained from the GA-BPNN model with experimental values at different strain rates: (A) 10^-1; (B) 10^-2; (C) 10^-3. GA-BPNN: Genetic algorithm-optimized back-propagation neural network.

Comparison of accuracy among different models

Figure 13 illustrates a comparison of the experimental values and the model-derived values from the three models under different deformation conditions. From the figure, it is evident that at a strain rate of 0.001 s^-1, all three models demonstrate relatively good accuracy. However, as the strain rate rises, accuracy of the Arrhenius model diminishes, while the BPNN and GA-BPNN models maintain a high level of accuracy.

Figure 13. Comparison of experimental values and model-derived values from three models at different strain rates: (A) 10^-1; (B) 10^-2; (C) 10^-3.

Figure 14 illustrates the relationship between the values derived from the model and the experimental values obtained through comparison of three models. The R² value for the GA-BPNN model exceeds that of other models, suggesting that GA-BPNN model provides a more accurate representation of the relationship between the experimental and model-derived values.

Figure 14. Comparison of model-derived values and experimental values from different models: (A) Training set of GA-BPNN model; (B) Testing set of GA-BPNN model; (C) Training set of BPNN model; (D) Testing set of BPNN model; (E) Arrhenius model. GA-BPNN: Genetic algorithm-optimized back-propagation neural network.

The R², RMSE, and MAE values for the model-derived values of the testing and training sets from the three models are shown in Table 2.

Table 2

Comparison of R², RMSE, and MAE among different models

Model	R 2	MAE	RMSE
Arrhenius data	92.12%	17.19	21.43
BPNN testing data	99.02%	5.47	6.78
BPNN training data	99.09%	5.44	8.78
GA-BPNN testing data	99.11%	5.40	6.48
GA-BPNN training data	99.15%	5.43	8.49

R ²: Coefficient of determination; RMSE: root mean square error; MAE: mean absolute error; BPNN: back-propagation neural network; GA-BPNN: genetic algorithm-optimized back-propagation neural network.

The GA-BPNN model demonstrated remarkable predictive accuracy and stability in this study. Specifically, the R² value for the testing set reached 99.11%, while that for the training set was 99.15%, indicating a high capability for explaining the variability of the target variable. The model also exhibited superior performance in terms of RMSE and MAE metrics, with a testing set RMSE of 5.40 and MAE of 6.48, as well as a training set RMSE of 5.43 and MAE of 8.49. These values are lower than those of the comparative models, highlighting the ability of GA-BPNN to provide more precise predictions, particularly in the context of complex data. Furthermore, the proximity of errors between the training and testing sets suggests that the model possesses good stability.

Furthermore, by comparing the predictive accuracy (R² values) of different aluminum-based materials during hot deformation (as shown in Table 3), it is evident that machine learning models, particularly BPNN and GA-BPNN, demonstrate significant advantages in accuracy. In contrast, the precision of traditional Arrhenius models is notably lower than that of the machine learning approaches. Furthermore, the accuracy achieved in this study is comparable to that of similar research. Overall, both GA-BPNN and BPNN models exhibit higher precision and stability in predicting the hot deformation of aluminum-based materials, particularly when addressing complex materials, thereby validating their superiority and potential for application.

Table 3

Comparative analysis of R² values for different hot deformation models in aluminum-based materials

Materials	Model	R 2	Ref.
Al-Mg alloys	BPNN	99.79%	[24]
Al-Zn-Mg-Cu-Zr alloys	BPNN	99.73%	[26]
Al-Cu-Mg-Ag alloys	BPNN	99.64%	[27]
Al-Cu-Mg-Ag alloys	Arrhenius model	97.62%	[27]
Al-Cu-Mg-Pb alloys	BPNN	99.90%	[28]
Al-Cu-Mg-Pb alloys	Arrhenius model	98.50%	[28]
Al-Cu-Mg-Pb alloys	Strain-compensated Arrhenius model	99.20%	[28]
Al-Cu-Mg-Pb alloys	JC model	97.60%	[28]
Al-Zn-Mg-Mn-Zr alloys	BPNN	99.83%	[29]
Al-Zn-Mg-Cu alloys	GA-BPNN	99.98%	[30]
Al-Zn-Mg-Cu alloys	Strain-compensated Arrhenius model	98.74%	[30]
Al matrix composite	GA-BPNN	99.11%	This work
Al matrix composite	BPNN	99.02%	This work
Al matrix composite	Strain-compensated Arrhenius model	92.12%	This work

R ²: Coefficient of determination; BPNN: back-propagation neural network; JC: Johnson-Cook; GA-BPNN: genetic algorithm-optimized back-propagation neural network.

The high precision of our BPNN and GA-BPNN models can be attributed to several critical factors that enhance their predictive accuracy. Firstly, the feature selection process focuses on three essential input parameters that are crucial for capturing the thermal deformation behavior of aluminum-based materials. The BPNN architecture, consisting of an input layer, one hidden layer with 15 neurons, and an output layer, strikes an optimal balance between complexity and accuracy. Additionally, the use of the GA for optimizing the BPNN parameters enhances performance significantly. The GA explores a diverse solution space and converges on optimal weights for the neural network. Overall, the combination of effective feature selection, a well-structured BPNN architecture, and a robust optimization approach through GA leads to the high predictive accuracy of our models, showcasing their innovation and strong applicability in predicting flow stress in aluminum-based materials.

Generalization ability of different models

Generalization ability is a core concept in machine learning, referring to a model’s capacity to make predictions on unseen new data. If a model performs well on the training set and possesses strong generalization ability, it can not only achieve excellent results on the training data but also maintain that level of performance on new, unknown data. This capability is crucial for ensuring prediction accuracy in practical applications. Therefore, models with strong generalization ability can adapt more effectively to new information, providing more reliable predictive outcomes.

To evaluate the generalization ability of the model, we performed compression tests at two temperatures, 723 and 773 K, utilizing a strain rate of 10^-3. This enabled us to obtain the high-temperature compression mechanical curves for the material. We selected points at intervals of 0.025 within the strain range of 0.05 to 0.2, utilizing the material’s strain rate, strain and temperature as feature inputs for the Arrhenius, BPNN, and GA-BPNN models. The predicted values from these three models were then compared with the actual curves, as illustrated in Figure 15. The accuracy metrics for the predicted values from the three models, including MAE, R², and RMSE, are presented in Table 4.

Figure 15. Comparison between the experimental data and the predicted values generated by various models on the validation: (A) Data of 723K; (B) Data of 773 K.

Table 4

Comparison of R², RMSE, and MAE among different models

Model	R 2	MAE	RMSE
Arrhenius	-92.98%	36.91	42.14
BPNN	35.81%	21.87	24.31
GA-BPNN	91.02%	7.83	9.09

R ²: Coefficient of determination; RMSE: root mean square error; MAE: mean absolute error; BPNN: back-propagation neural network; GA-BPNN: genetic algorithm-optimized back-propagation neural network.

It is evident that the predictions made by the GA-BPNN model align more closely with the actual values, showcasing a higher level of accuracy. This finding suggests that the GA-BPNN model exhibits strong generalization capacity, allowing it to accurately characterize the high-temperature flow stress of this heat-resistant AMC material.

Hot processing map based on the stress obtained from GA-BPNN model

To determine the appropriate hot processing parameters for the composite, we employed the stress value get from the GA-BPNN model to create hot processing map. It is crucial to select strain points at which the material flow remains relatively stable in order to effectively capture the behavior during the hot processing. The flow stress values that correspond to a true strain of 0.2 are selected from the data obtained from the GA-BPNN model to construct a hot processing map.

In the two-dimensional plane of temperature vs. strain rate, connecting points with the dissipation rate η produces contour lines for η, which constitute the power dissipation map, as shown in Figure 16A. The η is calculated by Equations (12)-(15).

Figure 16. (A) Power dissipation map (η); (B) Instability map (ξ); (C) Hot processing map of the composite.

By plotting the ξ values on the two-dimensional plane of T vs. ln$$ \dot{\varepsilon} $$, the instability map is obtained, as shown in Figure 16B. Using this instability criterion, the shaded region where ξ(ε) < 0 represents the instability zone. Overlaying the power dissipation map with the plastic instability map results in the hot processing map, as illustrated in Figure 16C. The instability region is observed to be below approximately 573 K, while the stable region is found above approximately 573 K.

Microstructure verification of hot processing map

To assess the precision of the established hot processing map, we characterized the microstructure of both the flow instability region and the flow stability region. Figure 17 presents the SEM images of the composite after deformation under different conditions. At 473 K, voids and cracks were observed at various strain rates. In contrast, at higher temperatures, the applied deformation localized in specific regions, leading to the development of distinct shear bands. The composite exhibited enhanced flow ability at elevated temperatures, significantly reducing the incidence of cracks and creating more favorable conditions for the hot processing of the composite.

Figure 17. SEM images of deformed samples under different conditions: (A) 473 K/10^-1; (B) 473 K/10^-2; (C) 473 K/10^-3; (D) 573 K/10^-1; (E) 573 K/10^-2; (F) 573 K/10^-3; (G) 673 K/10^-1; (H) 673 K/10^-2; (I) 673 K/10^-3. SEM: Scanning electron microscopy.

Furthermore, we conducted TEM characterization under the temperature of 673 K and a strain rate of 10^-3 in the hot stable processing region and compared it with the original sample, as shown in Figure 18. After hot deformation, the size of the nanostrips remained largely unchanged, with no significant cracks or voids observed. The interface between the nanostrips and the matrix remained well-bonded and clean, with no visible segregation at the grain boundaries and no significant additional phases formed. Additionally, the aluminum grains did not show abnormal growth, as illustrated in Figure 19. In summary, the composite exhibits good microstructural stability during deformation at elevated temperatures, contributing to the stability of the composite’s deformation.

Figure 18. Microstructural images of the composite before and after deformation at a strain rate of 10^-3 and temperature of 673 K: (A-C) show the state before deformation, while (D-F) illustrate the condition after deformation.

Figure 19. Statistical analysis of grain size of the composite before and after hot deformation: (A) before deformation; (B) after deformation.