Modeling-guided understanding microstructure effects in energy storage dielectrics
Abstract
Addressing the relationships between microstructures and properties is critical to the design of novel dielectric capacitors, which further enables widespread promising applications in electronic and electrical systems. The present review focuses on the role of different theoretical modeling techniques in understanding microstructural effects in energy storage dielectrics. State-of-the-art developments in the computational modeling of inorganics, polymers and their composite dielectrics are summarized. Diverse microstructural effects, including domain configurations, crystallization behavior and composite structures, are discussed with regards to different models. Theoretical modeling is not only essential for gaining fundamental insights into the underlying mechanisms behind experimental phenomena but can also be used to inversely engineer the design of dielectrics by prediction or optimization. Finally, to further promote innovative developments in dielectric capacitors, some future perspectives are provided to stimulate the in-depth consideration of the research paradigm between modeling and experiment.
Keywords
Introduction
With the rapid development of the global economy, the demand for energy continues to grow. Simultaneously, a series of problems, such as the fossil energy crisis, climate change and air pollution, have promoted the urgent need for high-performance materials for energy storage[1-4]. In existing electrical storage technologies, dielectric capacitors, which store and release energy by dipole polarization, have attracted increasing attention due to their fast charge/discharge rate and ultrahigh power density. As one of the most important electronic parts and components, dielectric capacitors have enabled widespread applications ranging from high-voltage direct-current transmission to high-power weapons, hybrid electric vehicles, medical equipment and other electrical/electronic systems[5,6]. Nevertheless, dielectrics with low energy density limit the further applications of capacitors under the increasing demands for miniaturization and portability. For example, the commercial dielectric biaxially oriented polypropylene (BOPP) usually exhibits a limited energy density of less than 2 J/cm3, leading to a large volume and weight of capacitors in electrical equipment[7]. In addition, more electric power applications are required to be used in harsh environments with high temperature and voltage conditions, which puts forward strict requirements for dielectric capacitors with higher dielectric strength and rated temperature[8-10]. Therefore, dielectric materials with high energy density, efficiency and stability are highly desirable for electrostatic energy storage devices.
A simple dielectric capacitor consists of two metal electrodes with a dielectric material between them[3,11]. As shown in Figure 1, without an applied electric field, the dipoles in dielectrics are random. When an electric field is applied during charging, the electrostatic energy is stored by the dipoles aligning along the direction of the applied electric field. After removing the electric field, the oriented dipoles tend to be randomly distributed again and the stored electrostatic energy is released into the load. Therefore, the recoverable energy density of a dielectric can be obtained by the integral of the polarization and the electric field:
Figure 1. (A) Schematic of dielectric energy storage during a charge/discharge process. Points I to II represent the charge process, while points II to III represent the discharge process. (B) Corresponding local dipole states in the dielectrics of points I, II and III.
where Pm and Pr are the maximum polarization and remnant polarization, respectively. The hysteresis response of polarization to an electric field leads to a partial energy loss (Uloss) in dielectrics, so the energy storage efficiency η for a dielectric can be expressed as η = Ue/(Ue + Uloss).
For linear dielectrics with the dielectric constant independent of the electric field, the stored energy storage density is given by:
where ε0, εr and Eb represent the vacuum dielectric constant, relative dielectric constant and breakdown strength, respectively. It can be seen from Equation (2) that in order to obtain high energy density, dielectrics with high polarization (i.e., a high dielectric constant) and breakdown strength and low dielectric loss are highly desired. However, one of the main problems of dielectrics is that the increase of Eb is usually at the expense of εr, due to the extremely high local electric field in dielectrics with high εr tending to weaken the polar dipoles, thereby making them easier to break[12,13]. Therefore, it is necessary to explore new strategies and rational designs to simultaneously improve the breakdown strength and dielectric constant of dielectric materials[14].
The intrinsic properties of a material are among the most basic principles to be considered in the design of energy storage dielectrics. Generally, according to the different responses of polarization to the applied electric field, dielectric materials can be divided into linear dielectrics, ferroelectrics, relaxor ferroelectrics and antiferroelectrics[15-17]. Their schematic dipoles, domain structures and polarization hysteresis loops are displayed in Figure 2. Linear dielectrics are characterized by linear polarization loops, high energy storage efficiency and negligible dielectric loss, but their low dielectric constant limits their further application. Ferroelectrics are widely studied due to their high dielectric constant, but their large remnant polarization is not conducive to achieving high energy density. Relaxor ferroelectrics and antiferroelectrics show excellent potential in optimizing energy storage efficiency and energy density, making them promising candidates for energy storage applications[4,18]. For example, there are nanodomains that can be freely flipped in relaxor ferroelectrics, resulting in lower remnant polarization and dielectric loss. Benefitting from the antiferroelectric-ferroelectric phase transition at high fields, antiferroelectrics exhibit double hysteresis loops, resulting in low coercive fields and high saturated polarization[19]. Therefore, the selection of suitable dielectrics can be used to effectively regulate the energy storage performance. On this basis, as illustrated in Figure 3, the diversity and complexity of microstructures at different scales in dielectrics open another perspective for regulating energy storage performance.
Figure 2. Schematic illustration of dipoles, domain structures and polarization hysteresis loops for linear dielectrics, ferroelectrics, relaxor ferroelectrics and antiferroelectric materials.
Figure 3. Schematic of the relationship between microstructures and ferroelectric properties and the role of theoretical modeling in guiding the multiscale design of microstructures in dielectrics.
In recent decades, a large number of studies have shown that regulating the microstructures in dielectrics represents a simple and effective method to improve the energy storage performance[6,20,21]. The variety of microstructures at different scales provides considerable opportunities for regulating performance, including domain configurations, crystallization behavior, composite structures and so on[3-5,11]. For example, at the nanoscale, ferroelectric materials respond to external field changes through domain switching. During the polarization switching process, the coupling effect between domains makes ferroelectrics exhibit nonlinear behavior, resulting in an increased energy loss. Some studies have shown that high energy density can be achieved by designing and controlling domain structures, such as the transformation of microscale domains into highly dynamic nanodomains[6,22]. When the scale increases to the micron level, taking inorganic dielectrics as examples, microstructural properties, such as grain size and grain boundaries, have a significant influence on the dielectric properties[23]. Fine ceramic grains with a uniform distribution can exhibit higher breakdown strength, leading to an enhancement in energy density.
With a further increase in scale, the heterogeneous structures in composite dielectrics have been proved to have substantial effects on dielectric properties by combining the advantages of all phases and some possible coupling effects, such as interfacial effects[21,24,25]. A great deal of composite structures have been designed to modulate the energy storage performance in experiments, such as core-shell, sandwich and multilayer structures, and polymer-based composites with inorganic nanofillers[7,26,27]. As a result, microstructural design has become a major research hotspot in the field of dielectric capacitors[1,28,29]. Beyond the limitations of material type, the diversity and complexity of microstructures at different scales provide a new level of design freedom for regulating the energy storage performance. However, this also brings more difficulties in clarifying the microstructure-property relationships and underlying mechanisms due to complicated and diverse influencing factors. Therefore, accurate knowledge of the relationships between the microstructures and properties of dielectrics is conductive to further promoting the development of high-performance dielectrics for energy storage.
With the continuous improvement of basic theories and the rapid development of computing power, theoretical modeling has become a burgeoning method in the exploration of the underlying microstructure-property relationships and the guidance of experimental optimization and design. In the field of dielectric materials for energy storage, complementary to experiments and characterization, ever more models are being developed to study microstructural effects. For example, density functional theory (DFT) and molecular dynamics (MD) can be used to determine some dielectric properties, including the electronic structure and intermolecular interactions, which are difficult to obtain experimentally[30-33]. In addition, some complex dielectric behavior, such as domain switching, dynamic processes of electric breakdown and interfacial effects, could be simulated by phase-field or finite element methods at the mesoscale[34-36]. In this review, we first briefly introduce the background to energy storage dielectrics. We then summarize some recent works on improving energy storage performance through microstructural design with the aid of theoretical modeling. These studies are organized into three areas, namely, inorganics, polymers and polymer-based composites. Finally, conclusions and future perspectives are provided. The main purpose of this review is to emphasize the importance of theoretical modeling and facilitate the cooperation of experiments and modeling.
Inorganic dielectrics
Compared with other dielectric materials, inorganic dielectrics have broad application prospects in energy storage due to their medium breakdown strength, high dielectric polarization and excellent temperature stability[4,37]. In recent decades, microstructural design in inorganic dielectrics, such as ferroelectrics, relaxor ferroelectrics and antiferroelectrics, have been extensively studied by domain engineering, grain regulation and the artificial design of core-shell or multilayer structures[22,38-44]. Although these microstructural designs can be achieved by advanced equipment and optimized fabrication processes, most of the underlying mechanisms of varying performance are poorly understood. Recently, theoretical modeling has gradually become an effective tool for clarifying microstructure-property relationships, including polymorphic nanodomain, grain and interfacial effects[35,45-48]. Here, some microstructural effects across different scales on the polarization and breakdown strength of inorganic dielectrics are analyzed from a modeling perspective.
At the nanoscale, domain configuration and switching behavior strongly affect the macroscopic ferroelectric properties[49]. Generally, microdomains in ferroelectrics tend to show strong ferroelectric hysteresis and large remnant polarization, resulting in high dielectric loss and low energy storage efficiency. On the contrary, weakly coupled polar nanodomains in relaxor ferroelectrics are highly dynamic and sensitive to the applied electric field. Therefore, relaxor ferroelectrics exhibit slim Polarization-Electric Field (P-E) loops with modest maximum polarization and negligible remnant polarization in the process of charging and discharging[50,51]. In recent decades, in order to achieve high energy density, increasing attention has been paid to the construction of nanodomains to promote the transformation of ferroelectrics into relaxor ferroelectrics[52-55]. However, due to the complexity of domain structures at the nanoscale, the reasonable construction of nanodomains has become a significant challenge in experimental design.
Based on Landau’s theory, a phase-field model was properly developed to simulate domain structures and switching under external stimuli[56,57]. For instance, Pan et al.[58] proposed a polymorphic nanodomain strategy based on phase-field simulations. First, the domain structures of solid solutions were simulated, as shown in Figure 4A and B. It was found that the 0.45BiFeO3-0.55SrTiO3 solid solution possesses rhombohedral domains while the 0.20BiFeO3-0.25BaTiO3-0.55SrTiO3 ternary system has a disordered structure with coexisting rhombohedral and tetragonal nanodomains. These polymorphic nanodomains with competitive free energy in ternary systems can effectively weaken the polarization anisotropy and reduce the domain switching barrier, leading to a higher polarization and lower dielectric loss. The energy density and efficiency of different components were then calculated to find the best composition in this system. Finally, under the guidance of simulation results, the optimized 0.25BiFeO3-0.30BaTiO3-0.45SrTiO3 composition exhibited minimized hysteresis while maintaining high polarization and achieved a giant energy density of 112 J/cm3 with a high energy efficiency of ~80%.
Figure 4. Simulated domain structures of (A) 0.45BiFeO3-0.55SrTiO3 and (B) 0.20BiFeO3-0.25BaTiO3-0.55SrTiO3[58]. (C) Simulated domain structure of BaTiO3 and BiFeO3 thin films under mismatch strains of 2% and -2%. Black and white colors represent domains with stronger out-of-plane polarization components, while other colors represent domains with stronger in-plane polarization components[59]. (D) Free energy surfaces of BaTiO3 and BiFeO3 under mismatch strains of 2% and -2%, respectively[59]. (E) Breakdown path in dielectrics with different grain sizes[61]. (F) Local electric field distribution of virtual samples with different shell fractions under an external applied voltage of 200 V[68]. (G) Finite element simulation of the distribution of stress and elastic energy density in a single layer of a multilayer ceramic capacitor[72]. (H) Simulated development of electric trees in Ba0.7Ca0.3TiO3/BaZr0.2Ti0.8O3 multilayer films with different total thicknesses[74]. (I) Simulated evolution of electric trees in BaZr0.15Ti0.85O3/BaZr0.35Ti0.65O3 multilayer films with different stacking periodic numbers (N)[77].
In domain engineering, besides forming solid solutions, strain engineering is also widely used to tune the domain behavior. For example, Wang et al.[59] used the phase-field method to calculate free energy surfaces and predict the domain structures of ferroelectric oxide thin films under mismatch strains of 2% and -2%. Taking BaTiO3 as an example, as shown in Figure 4C and D, a BaTiO3 thin film under a 2% equibiaxial mismatch strain shows orthorhombic in-plane domains and the surface free energy is at a maximum when the polarization is along the out-of-plane [001] and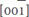 
directions. Alternatively, a BaTiO3 thin film under -2% equibiaxial mismatch strain shows out-of-plane tetragonal domains and the surface free energy is at maximum when the polarization is along the in-plane 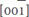, [010], 
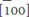and 
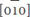directions. Therefore, in-plane tensile strain reduces remanent polarization and out-of-plane tensile strain increases saturated polarization. Based on the predicted results of the strain effects on the domain structure and polarization, a bending strategy for optimizing the charge/discharge density was proposed. PbZr0.52Ti0.48O3 with a high energy density of 182 J/cm3 was then obtained by bending the substrate up and down during the charge/discharge process.
On a larger scale than the domain structure, crystallization behavior is another research hotspot[4,15]. For example, the grain size has a significant effect on dielectric properties, especially for the breakdown strength. In inorganic dielectrics, the relationship between the breakdown strength and grain size can be empirically described as[60]:
where G is the grain size. A decrease in grain size leads to an increase in grain boundary density, which can prevent the further migration of charge carriers and improve the breakdown strength. Furthermore, due to the quadratic correlation to the energy density, increasing breakdown strength can improve the energy density more effectively than increasing the dielectric constant. Increasingly more researchers have struggled to further elucidate the effect of crystallization behavior on the breakdown process[41,47,61]. However, it is difficult to characterize the breakdown process by experimental techniques because the dielectric breakdown is a complex nonequilibrium process.
Generally, the breakdown is often accompanied by a conductive path throughout the materials; thus, dynamic simulations of the breakdown path can help to better analyze the dielectric breakdown process[62]. As a result, many theoretical models have been proposed to simulate the generation and expansion of electric trees, such as the dielectric breakdown[63,64] and electron avalanche models[65]. For example, Cai et al.[61] established a phase-field model to study the effect of grain size on the breakdown path. As shown in Figure 4E, during the dielectric breakdown process, the breakdown path is hindered by the grain boundary due to the higher breakdown energy required. Therefore, inorganic dielectrics with fine grains show higher breakdown strength. Furthermore, the concept of core-shell dielectric ceramics was proposed, which is based on the use of highly insulating materials, such as SiO2 and Al2O3[66,67], to coat ferroelectric ceramic grains. Wu et al.[68] employed the finite element method to investigate the effect of core-shell structures on dielectric properties in terms of the electric field distribution. It can be seen from Figure 4F that for a given electric field, the local field uniformity is enhanced with increasing shell fraction, which is conducive to higher dielectric breakdown strength. Likewise, Yuan et al.[69] designed core-shell BaTiO3-Bi(Mg0.5Zr0.5)O3@SiO2 relaxor ferroelectrics and found that the introduction of SiO2 reduced the grain size of BaTiO3-Bi(Mg0.5Zr0.5)O3.
Simultaneously, finite element simulations have showed that SiO2 forms interfacial barriers to prevent the rapid development of electric trees. In addition, the electrostrictive strain under the external electric field also seriously affects the electromechanical breakdown of dielectric ceramics[70]. Studies have shown that due to the strong electrostrictive anisotropy, the electrostrictive strain produced by grains with different orientations varies greatly[71]. Recently, Li et al.[72] performed finite element simulations to investigate the effect of grain orientation on electric field-induced strain in textured ceramics. As displayed in Figure 4G, compared with other ceramics, <111>-textured ceramics exhibit much lower stress, local displacement and elastic energy, which is excepted to enhance the breakdown strength. To experimentally realize this concept, the authors fabricated high quality <111>-textured Na0.5Bi0.5TiO3-Sr0.7Bi0.2TiO3 ceramics by a template grain growth method. The <111>-textured ceramics show lower electric field strain, leading to a decrease in the failure probability and an increased breakdown strength of ~103 MV/m, which was ~65% higher than that of the corresponding randomly oriented ceramics.
In addition, the artificial design of multilayer inorganic dielectrics by stacking two layers of different components has been widely studied due to the existence of hierarchical interfaces in the multilayer structure[73-76]. Interfacial engineering has been shown to be effective in enhancing dielectric energy density. Simultaneously, researchers further used computational simulations to explain how the interface between the dielectric layers affects the growth of electric trees and the distribution of the electric field. For instance, Sun et al.[74] prepared multilayer films of Ba0.7Ca0.3TiO3/BaZr0.2Ti0.8O3 dielectrics and used theoretical models to study the effects of interfacial density and total multilayer film thickness on the dielectric breakdown. The development of electric trees was simulated by the finite element method for the multilayer films with the same period thickness with a different total thickness, as shown in Figure 4H. It can be seen from the simulation results that with increasing total thickness of the multilayer films, the suppression effect of the interface on the electric trees is enhanced. This phenomenon can be attributed to the increase in interfacial density, which can boost the ability to prevent the growth of electric trees. Analogously, Fan et al.[77] prepared a BaZr0.15Ti0.85O3/BaZr0.35Ti0.65O3 multilayer thin film by controlling the number of interfaces under a given total thickness. As presented in Figure 4I, the development of electric trees was simulated based on the finite element method. The simulation results can be explained from two perspectives. Firstly, the existence of the interface can block the electric trees penetrating in the film. Secondly, interfacial coupling becomes stronger with increasing interface number, which may weaken the interfacial blocking effect. Therefore, the breakdown strength achieves its maximum value when the period number N is 6.
As mentioned above, many studies have realized improved energy density by optimizing microstructures through domain engineering, grain engineering and multilayer structures. With the aid of theoretical modeling, the influence of microstructural changes on dielectric properties is analyzed, including polarization switching and dielectric breakdown. However, the low breakdown strength is still the main factor limiting for the increase in the energy storage density of inorganic dielectrics. Simultaneously, alleviating and breaking the coupling between polarization and breakdown strength are key challenges for further performance enhancement. The combination of theoretical modeling and experimental characterization is expected to explore unrevealed mechanisms and accelerate the discovery of novel inorganic dielectrics with excellent energy storage properties.
Polymer dielectrics
Compared with inorganic dielectrics, polymer dielectrics have the advantages of high intrinsic breakdown strength, good flexibility, lightweight and easy processing[3,8]. In recent years, to replace commercial BOPP film capacitors for device miniaturization and cost reduction, extensive research has been carried out to discover or create new polymer systems, such as ferroelectric polymers (e.g., PVDF, PVDF-HFP and PVDF-TrFE) and linear polymers (e.g., PI, PEI and PS)[26]. Meanwhile, researchers have found that microstructural regulation could be a direct and effective approach for improving the energy storage performance, such as molecular chain modification, crystalline/amorphous phase behavior and multilayer structures[78-83]. A growing number of studies have made excellent progress under the guidance of theoretical modeling. Here, we present several representative works to summarize the role of theoretical modeling in addressing the influence of microstructural effects on dielectric properties.
At the molecular level, DFT and MD are widely used to study the behavior of molecular chains in polymers[84,85]. Such behavior includes thermodynamic details, the interactions between molecular chains and the optimized molecular structure of the polymers[86-89]. For example, Wang et al.[90] used DFT simulations to investigate the role played by -OH functional groups and water molecules in two short-chain polyethylene oligomers (o-PE), as shown in Figure 5A. The dielectric constant increases from 2.3 for o-PE to 4.3 for o-PE-OH-2H2O due to the contribution of electrons and ions. Further simulation results have shown that the use of functionalized polymer chains is an effective path to improving the dielectric constant of polymers. Additionally, Thakur et al. reported that by blending poly(arylene ether urea) (PEEU, εr = 4.7) and aromatic polythiourea (ArPTU, εr = 4.4) to form a nanomixture, the resulting blend exhibited a very high dielectric constant of 7.5[91]. As displayed in Figure 5B, the simulation results indicated that mixing of the two polymers causes an increase in the interchain spacing due to the mismatch of the polymer unit length and dipolar functional group locations. The increase in molecular chain spacing introduces additional free volume, which allows the dipole to rotate and align better with the electric field, thereby enhancing the dielectric response.
Figure 5. (A) Optimized structures of o-PE, o-PE-OH, o-PE-OH-H2O and o-PE-OH-2H2O, where black, white and red spheres represent C, H and O atoms, respectively[90]. (B) From left to right, top view of simulation unit cells of ArPTU, blend with a 1:1 PEEU:ArPTU ratio and PEEU, respectively[91]. (C) Simulated microscopic local electric field distribution of ΔE in polymer blends with random and ordered distributed amorphous phases[95]. (D) Internal field distribution inside the relaxor ferroelectric polymer blend before (left) and after int-biased (right) at 50 MV/m[96]. (E) Distribution of local electric field along the direction of the applied field in Co/Ter multilayer films with eight layers (top) and their breakdown evolution (bottom)[97]. (F) Breakdown evolution for multilayer films with different layers[98].
It should be noted that modifying molecular chain structures is a costly and complex process. Polymer blending is a general and scalable strategy to tune the ferroelectric behavior by controlling the composition and crystallization behavior[31,92-94]. For example, Zhang et al.[95] proposed a two-step process to generate a random distribution of P(VDF-TrFE) crystalline phases and break the coherent coupling of the ferroelectric domain between ordered crystalline phases. By performing phase-field simulations, the local electric fields ΔE in polymer blends with random and ordered configuration are simulated to find the underlying mechanism, as seen in Figure 5C. The simulation results demonstrated that the random configuration is much more capable of reducing the ΔE in the crystalline phase and is conducive to the inversion of the dipole, resulting in an ultrahigh electrical energy storage density of 20.4 J/cm3 at 720 MV/m. In addition, Qian et al.[96] employed phase-field simulations to understand the effect of the internal DC bias field. In this work, they introduced a ferroelectric component in the nanophase form into the relaxor polymer matrix to establish an internal DC bias field in the polymer blends by controlling the properties of ferroelectric components. Figure 5D shows the distribution of remnant electric field established under an external of ΔE = 100 MV/m in the relaxor polymer matrix, which is unbiased and int-biased with Ebias of 50 MV/m. It can be seen from the simulation results that the int-biased blends exhibit a marked internal electric field in the terpolymer matrix due to the strong remnant polarization of the ferroelectric copolymer. As a result, the int-biased blends exhibit a high electrocaloric effect at low fields.
At larger scales, multilayer structures have been taken as another effective method to adjust the dielectric properties of polymer dielectrics[80]. With the assistance of theoretical modeling, some possible physical mechanisms are becoming clear, which greatly promote the design of novel multilayer structures. For example, dielectric or electrical mismatch among different polymer layers could cause the redistribution of the local electric field. Furthermore, the interfacial phase with a high dielectric constant induced by Maxwell-Wagner-Sillars interfacial polarizations changes the charge behavior, electrical conduction and electric polarization at the interface. Recently, Jiang et al.[97] fabricated P(VDF-HFP)/P(VDF-TrFE-CFE) multilayered films with extremely high charge/discharge efficiency (80%-85%) and high discharge energy density (~20 J/cm3) through a non-equilibrium process. Phase-field simulations revealed the superiority of the multilayer structure in energy storage.
The top of Figure 5E exhibits the distribution of the local electric field along the direction of the applied field in multilayered films with eight layers. The interfacial phase with a high dielectric constant substantially weakens the local electric field at the interface, which can hinder the migration of carriers and greatly suppress the conduction loss. As the three-dimensional simulated breakdown path at the bottom of Figure 5E shows, the breakdown paths propagate faster in the nanocomposites with less layers than those with more layers and hence a higher breakdown strength was obtained with an increasing number of layers. Similarly, Zhang et al.[98] used a stacking method to prepare a series of alternating multilayer films with different layers of PMMA and P(VDF-HFP). A phase-field model was employed to determine the reasons for the improved performance by simulating the growth of electric trees in the multilayer films, as shown in Figure 5F. Deep traps at the interfaces between PMMA and P(VDF-HFP) can capture charge carriers and limit their further migration. In addition, the dielectric mismatch between layers can reduce the electric field in the P(VDF-HFP) layer and avoid early breakdown. Thus, with an increasing number of layers, the longitudinal growth and lateral expansion of the electric trees were inhibited. Therefore, optimization of the topological structure, phase composition, layer thickness and layer numbers of multilayer films can improve the energy storage performance of materials.
As summarized above, theoretical modeling has gradually become a common method in understanding microstructure-property relationships. By combining DFT, MD and the phase-field method, researchers have made significant progress in the microstructural design of polymer dielectrics, such as molecular chain modifications, polymer blending and multilayer structures. However, there are still some challenges facing polymer dielectrics. For example, the low dielectric constant of the polymer limits the energy density and the deterioration of polymer performance at high temperature is another important factor restricting the application of polymer dielectrics. In addition, there is a lack of in-depth analysis of some mechanisms or effects, such as the interfacial effect between crystalline and amorphous phases and high-temperature effects. In the future, it will be necessary to combine the results of theoretical calculations with experimental rules to further explore the relationship between microstructure and properties.
Polymer-based composite dielectrics
Polymer-based composite dielectrics have the potential to combine both the advantages of the high dielectric constant of ceramic fillers and the high breakdown strength of polymer matrices and have attracted significant attention for energy storage applications[27,99]. Polyvinylidene fluoride and its copolymers and terpolymers are currently the most widely studied matrices in polymer-based composite dielectrics due to their high breakdown strength and medium dielectric constant[100,101]. Various ceramics with high dielectric constants are used as filler candidates, including BaTiO3, SrTiO3, TiO2 and so on[102-105]. Furthermore, microstructural modulation has been proved to be a practical method to improve the dielectric constant and breakdown strength of nanocomposite dielectrics, such as interfacial modification[106-108], nanofiller structures and distribution[109-113] and multilayer structures[75,114,115]. Simultaneously, the rapid development of theoretical modeling has brought convenience for the efficient design of new nanocomposite structures[34,85,116,117]. The role of theoretical modeling in the materials selection and microstructural design of polymer-based composite dielectrics is discussed in this section.
When nanofillers with high specific surface area are added into the polymer matrix, a large number of interfacial regions are formed, which may alter the macroscopic properties of the composites[118,119]. For example, the existence of interfaces may change the distribution of space charges, thereby improving polarization. In addition, the interfaces in composites with a low content of nanofillers may act as traps to limit the migration of charges, resulting in a decrease in charge mobility and suppressed leakage current. Nevertheless, the interfacial regions in polymer-based composites with a high volume fraction of nanofillers are highly possible to overlap, which may lead to the aggregation of space charge and improved electrical conductivity. Therefore, a full understanding of the interface is favorable for tailoring the properties of composite dielectrics.
Although some theoretical interfacial models, such as Lewis’s model[118] and Tanaka’s model[120], have been proposed to explain the interfacial effects on nanocomposites, quantitative studies of interface-property relationships are still lacking. Recently, Shen et al.[121] employed theoretical modeling to investigate the interfacial space charge effects on the dielectric response of polymer nanocomposites with randomly distributed and aggregated nanoparticles, as shown in Figure 6A. When the nanofillers aggregate, a connected space charge region is formed, resulting in a high dielectric constant but also high dielectric loss and local electrical conductivity. In addition, modeling results indicate that the dielectric constant mismatch between the matrix and fillers can cause an obvious inhomogeneous local electric field at the interface, which can lead to a decrease in breakdown strength.
Figure 6. (A) Equilibrium distributions of space charge in a polymer nanocomposite with randomly distributed and aggregated nanoparticles[121]. (B) Map of breakdown strength with different interfaces in PVDF-BaTiO3 nanocomposites[123]. (C) Definition of the microstructure dataset by assigning different length ratios of the nanofillers[124]. (D) Datasets of breakdown strength and the effective relative permittivity from high-throughput calculations[124]. (E) Simulated development of electric trees in polymer nanocomposites without and with aluminosilicate nanosheets (MMT)[130]. (F) Simulated development of electric trees in polymer nanocomposites with different nanofiller configurations[131]. (G) Distribution of charge density in different multilayered nanocomposites[134].
The introduction of low dielectric constant materials on the surface of high dielectric constant nanofillers as shell layers is an effective method for alleviating electric field distortion. For instance, Pan et al.[122] designed novel core-double-shell-structured BaTiO3@TiO2@Al2O3 nanofibers and incorporated them into a PVDF matrix. The finite element method was used to illustrate the effect of nanofibers with different structures on the local electric field distribution. It was found that BaTiO3@TiO2@Al2O3 nanofibers with a multilayer hierarchical interface can alleviate the local electric field and reduce leakage current obviously compared with composites with only BaTiO3 or BaTiO3@TiO2 nanofibers. Furthermore, in order to better understand the effect of microscopic interfacial features on the macroscopic properties, Shen et al.[123] developed a data-driven interface design strategy based on high-throughput phase-field simulations to investigate the interfacial effect on dielectric properties. In this model, an interfacial phase with different thicknesses and permittivity was introduced to optimize the dielectric constant and breakdown strength of nanocomposites. As shown by the local electric field displayed in Figure 6B, the interface with higher or lower permittivity causes an obvious electric field distortion, leading to fast propagation of the breakdown path and early failure under a high electric field. Based on the calculation results, an interface optimized strategy with a core-shell structure in the PVDF-BaTiO3 nanocomposite with 0.3r ≤ d ≤ r and 0.026εfiller ≤ εinterface ≤ 0.08εfiller was obtained. This interface design strategy can also be applied to study interfacial issues in other functional nanocomposites.
The shape and orientation of nanofillers also strongly influence the dielectric properties of nanocomposites[110,124,125]. For example, one-dimensional nanofibers with a high aspect ratio increase the effective dielectric constant of the nanocomposites more obviously compared with zero-dimensional nanoparticles, and the enhancement effect is more significant when the nanofibers are parallel to the electric field direction[126]. A higher breakdown strength can be achieved in nanocomposites filled with highly insulating two-dimensional nanosheets perpendicular to the electric field direction[10,111,112]. In order to comprehensively understand the effect of nanofiller features on the local electric field distribution and breakdown strength in nanocomposites, high-throughput simulations based on a phase-field model were developed. As displayed in Figure 6C, Shen et al.[124] defined a microstructural dataset for nanocomposites by assigning different length ratios of the nanofillers. The breakdown strength and effective relative permittivity were then calculated with different microstructures, as shown in Figure 6D. The simulation results indicated that the shape and orientation of the nanofillers significantly affect the energy storage performance. For example, with the same volume fraction of the nanofiller, vertically distributed nanofibers make the electric field more concentrated at the ends of the fibers, resulting in higher polarization. In contrast, parallel nanosheets make the electric field more dispersed, which hinders the expansion of the breakdown phase. Therefore, the incorporation of parallel nanosheets into the polymer could increase the breakdown strength, while the incorporation of vertical nanofibers is beneficial for increasing the effective dielectric constant.
Based on the above conclusions, many hierarchical structures have been designed to improve energy storage performance[127-129]. For example, Luo et al.[130] proposed an effective strategy that utilizes superhierarchical structures and gradient interfaces in inorganic/organic nanocomposites to achieve ultrahigh energy density. The dynamic breakdown process of polymer nanocomposites without and with aluminosilicate nanosheets (MMT) was simulated by the phase-field method. As shown in Figure 6E, although BaTiO3 nanoparticles with a layer of Al2O3 and SiO2 (BT@AS) can improve polarization, their lower intrinsic breakdown makes the nanocomposites easier to breakdown. When BT@AS particles are located around MMT nanosheets, the nanosheets obviously change the direction of the breakdown path, thereby playing a role in hindering the propagation of the electric trees. As a result, a high energy density of 20 J/cm3 and a high efficiency of 84% at a low electric field of 510 MV/m were achieved.
The design of three-dimensionally-distributed nanofillers has been proved to have excellent potential in tuning the energy storage properties of nanocomposites[3]. For example, the gradient distribution of nanofillers can be realized by adjusting the content in the out-of-plane direction and modeling has further verified the superiority of gradient structures in inhibiting charge injection and preventing the growth of electric trees. Recently, Jiang et al.[131] proposed polymer nanocomposites with a novel interpenetrating gradient structure by cofilling a PVDF matrix with Ba(Zr0.21Ti0.79)O3 fibers and BN nanosheets. Figure 6F presents the development of electric trees in nanocomposites simulated by the phase-field method. It can be seen that gradient distributed fillers (G-BZT_nfs and G-BNNS) are more effective in hindering the development of the breakdown phase than randomly distributed fillers (R-BZT_nfs). Furthermore, G-BZTBNNS nanocomposites with an interpenetrating gradient structure combine the advantages of G-BZT_nfs and G-BNNS nanocomposites, resulting in enhanced polarization and breakdown strength and suppressed dielectric loss.
In addition, the strategies of sandwich or multilayer structures also work in polymer-based nanocomposites[75,132]. The distribution of a local electric field in multilayered nanocomposite dielectrics can be adjusted by controlling the filler content in different layers. For instance, Wang et al.[133] prepared a sandwich-structured dielectric nanocomposite with a much improved breakdown field and energy density. Finite element simulations showed the redistribution of the electric field due to the different volume fractions of BaTiO3 in each layer, with the weak electric field at the interface blocking the growth of the electric trees. Furthermore, Jiang et al.[134] fabricated multilayered polymer nanocomposites with interfaces of high structural integrity by a nonequilibrium processing method. They then employed a phase-field model to understand the influence of the interfaces between adjacent dielectric layers on the charge distribution in nanocomposites, as displayed in Figure 6G. In multilayer nanocomposites, polarized ions at the interface induce a strong depolarization field opposite to the applied electric field, which lowers the local electric field and increases the height of the potential barrier at the dielectric/dielectric interface. Moreover, compared with the pure P(VDF-HFP) layer close to the electrodes, the charge injection of the P(VDF-HFP)/BaTiO3 composite layer close to the electrodes is more serious. Therefore, multilayered nanocomposites with a pure polymer layer close to the electrodes can exhibit lower leakage current and higher breakdown strength.
Through the reasonable design of microstructures with approaches such as interfacial modification, nanofiller structures and distribution, and multilayer structures, nanocomposite materials have made remarkable progress in enhancing energy density. With the aid of theoretical modeling, some underlying mechanisms and foundational relationships between microstructures and properties have gradually become clear. However, it is still too early to challenge the status of the BOPP capacitor because many issues, including poor charge/discharge efficiency and temperature stability, still exist in current polymer-based nanocomposites. Furthermore, the understanding of interfacial effects at the molecular and atomic levels is also insufficient. In the future, multiscale modeling and machine learning may become powerful weapons to break through these bottlenecks.
Conclusions and outlook
As reviewed in this article, modeling has become an important component in the research and development of energy storage dielectrics from inorganics and polymers to their composites. The combination of experiment and modeling has yielded impressive developments in not only understanding the relationships between the microstructures and properties of dielectrics, but also in sparking novel design ideas for new dielectrics. However, to further enhance the guiding role of theoretical modeling in the process of materials discovery and innovation, the following strategies deserve increased attention.
Multiscale modeling
With the developments in basic theory and computing technology, many modeling methods at different scales have been widely used for materials research, including DFT, MD and phase-field simulations. However, these different models usually focus on one or limited scales of resolution. It remains highly challenging to simulate a multiscale process or hierarchical phenomenon in dielectrics using a single-scale modeling approach, such as the dielectric breakdown process and relaxation behavior. Therefore, to study one dielectric system at different levels of resolution and complexity with sufficient accuracy and appropriate efficiency, it is necessary to develop multiscale modeling approaches that bridge microscopic and macroscopic models. Such models will help us to further understand the direct relationships between microstructures and properties from an atomic/molecular level to macroscopic dielectric performance, such as linking P-E loops to atomic displacements or chemical fluctuations. However, some challenges remain to achieve the multiscale modeling of dielectric behavior, including multiscale theories and algorithms.
Microstructure-property databases
In recent decades, partly propelled by the Materials Genome Initiative, database technology has been extensively studied and developed, with many materials databases now available and open to the public, such as the Materials Project and AFLOWLIB. However, most databases focus on the information of chemical elements and crystal or molecular structures and thus lack microstructural data, such as domain configurations, polycrystalline structure and multiphase distribution, in the field of dielectrics. It is therefore imperative to build databases containing microstructures and the corresponding macroscopic properties of dielectrics, which could be important data for supporting the intelligent investigation of microstructure-property relationships. Due to the image data type of complicated microstructural information, some critical technologies still need to be improved. One of the major challenges is how to automatically acquire massive microstructural images from experiments and precisely generate virtual microstructures by algorithms. Other challenges include image storage and management technology and information mining technology.
Machine learning models
Under the data-driven research paradigm, machine learning is regarded as a promising tool for the discovery and design of novel materials for a broad range of applications. When studying microstructural effects on macroscopic properties, machine learning could also be a powerful approach for performance prediction, microstructure optimization and inverse design. In view of the diversity and complexity of microstructures, some updated technologies in machine learning models need to be developed. For example, establishing effective descriptors to characterize the graphical features of different microstructures with numerical data is the basis of finding mathematical expressions, predicting dielectric properties and designing new microstructures. Furthermore, introducing intelligent algorithms into the whole process of experimental preparation and characterization could make materials research and development faster, less expensive and more efficient.
Declarations
Authors’ contributionsConceived and designed the manuscript: Shen ZH
Drafted and revised the manuscript: Shen ZH, Wang J
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was supported by the Major Research Plan of NSFC (Grant No. 92066103), the NSF of China (Grant No. 52002300), the Young Elite Scientists Sponsorship Program by CAST (Grant No. 2019QNRC001).
Conflicts of interestBoth authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The author(s) 2021.
REFERENCES
1. Yao Z, Song Z, Hao H, et al. Homogeneous/inhomogeneous-structured dielectrics and their energy-storage performances. Adv Mater 2017;29:1601727.
2. Luo H, Zhou X, Ellingford C, et al. Interface design for high energy density polymer nanocomposites. Chem Soc Rev 2019;48:4424-65.
3. Prateek, Thakur VK, Gupta RK. Recent progress on ferroelectric polymer-based nanocomposites for high energy density capacitors: synthesis, dielectric properties, and future aspects. Chem Rev 2016;116:4260-317.
4. Yang L, Kong X, Li F, et al. Perovskite lead-free dielectrics for energy storage applications. Prog Mater Sci 2019;102:72-108.
5. Wang G, Lu Z, Li Y, et al. Electroceramics for high-energy density capacitors: current status and future perspectives. Chem Rev 2021;121:6124-72.
6. Pan H, Kursumovic A, Lin YH, Nan CW, MacManus-Driscoll JL. Dielectric films for high performance capacitive energy storage: multiscale engineering. Nanoscale 2020;12:19582-91.
7. Wei J, Zhu L. Intrinsic polymer dielectrics for high energy density and low loss electric energy storage. Prog Polym Sci 2020;106:101254.
8. Tan DQ. Review of polymer-based nanodielectric exploration and film scale-up for advanced capacitors. Adv Funct Mater 2020;30:1808567.
9. Zhang G, Li Q, Allahyarov E, Li Y, Zhu L. Challenges and opportunities of polymer nanodielectrics for capacitive energy storage. ACS Appl Mater Interfaces 2021;13:37939-60.
10. Li Q, Chen L, Gadinski MR, et al. Flexible high-temperature dielectric materials from polymer nanocomposites. Nature 2015;523:576-9.
11. Zhang X, Li BW, Dong L, et al. Superior energy storage performances of polymer nanocomposites via modification of filler/polymer interfaces. Adv Mater Interfaces 2018;5:1800096.
12. Hu H, Zhang F, Luo S, Chang W, Yue J, Wang CH. Recent advances in rational design of polymer nanocomposite dielectrics for energy storage. Nano Energy 2020;74:104844.
13. McPherson JW, Kim J, Shanware A, Mogul H, Rodriguez J. Trends in the ultimate breakdown strength of high dielectric-constant materials. IEEE Trans Electron Devices 2003;50:1771.
14. Chen Q, Shen Y, Zhang S, Zhang Q. Polymer-based dielectrics with high energy storage density. Annu Rev Mater Res 2015;45:433-58.
15. Palneedi H, Peddigari M, Hwang GT, Jeong DY, Ryu J. High-performance dielectric ceramic films for energy storage capacitors: progress and outlook. Adv Funct Mater 2018;28:1803665.
16. Veerapandiyan V, Benes F, Gindel T, Deluca M. Strategies to improve the energy storage properties of perovskite lead-free relaxor ferroelectrics: a review. Materials (Basel) 2020;13:E5742.
17. Yang Z, Du H, Jin L, Poelman D. High-performance lead-free bulk ceramics for energy storage applications: design strategies and challenges. J Mater Chem A Mater 2021;9:18026-85.
18. Pramanick A, Nayak S. Perspective on emerging views on microscopic origin of relaxor behavior. J Mater Res 2021;36:1015-36.
19. Liu Z, Lu T, Ye J, et al. Antiferroelectrics for energy storage applications: a review. Adv Mater Technol 2018;3:1800111.
20. Li F, Zhang S, Damjanovic D, Chen LQ, Shrout TR. Local structural heterogeneity and electromechanical responses of ferroelectrics: learning from relaxor ferroelectrics. Adv Funct Mater 2018;28:1801504.
21. Yao FZ, Yuan Q, Wang Q, Wang H. Multiscale structural engineering of dielectric ceramics for energy storage applications: from bulk to thin films. Nanoscale 2020;12:17165-84.
22. Pan H, Ma J, Ma J, et al. Giant energy density and high efficiency achieved in bismuth ferrite-based film capacitors via domain engineering. Nat Commun 2018;9:1813.
23. Li D, Zeng X, Li Z, et al. Progress and perspectives in dielectric energy storage ceramics. J Adv Ceram 2021;10:675-703.
24. Zhang H, Wei T, Zhang Q, et al. A review on the development of lead-free ferroelectric energy-storage ceramics and multilayer capacitors. J Mater Chem C Mater 2020;8:16648-67.
25. Huang X, Sun B, Zhu Y, Li S, Jiang P. High-k polymer nanocomposites with 1D filler for dielectric and energy storage applications. Prog Mater Sci 2019;100:187-225.
26. Huan TD, Boggs S, Teyssedre G, et al. Advanced polymeric dielectrics for high energy density applications. Prog Mater Sci 2016;83:236-69.
27. Fan B, Zhou M, Zhang C, He D, Bai J. Polymer-based materials for achieving high energy density film capacitors. Prog Polym Sci 2019;97:101143.
28. Jiang Y, Zhou M, Shen Z, et al. Ferroelectric polymers and their nanocomposites for dielectric energy storage applications. APL Materials 2021;9:020905.
29. Sun Z, Wang Z, Tian Y, et al. Progress, outlook, and challenges in lead-free energy-storage ferroelectrics. Adv Electron Mater 2020;6:1900698.
30. Dong R, Ranjan V, Nardelli MB, Bernholc J. Atomistic simulations of aromatic polyurea and polyamide for capacitive energy storage. Phys Rev B 2015;92:024203.
31. Zhang Q, Chen X, Zhang B, et al. High-temperature polymers with record-high breakdown strength enabled by rationally designed chain-packing behavior in blends. Matter 2021;4:2448-59.
32. Saiz F, Quirke N. The excess electron in polymer nanocomposites. Phys Chem Chem Phys 2018;20:27528-38.
33. Shi N, Ramprasad R. Local properties at interfaces in nanodielectrics: an ab initio computational study. IEEE Trans Dielectr Electr Insul 2008;15:170.
34. Shen ZH, Wang JJ, Jiang JY, et al. Phase-field modeling and machine learning of electric-thermal-mechanical breakdown of polymer-based dielectrics. Nat Commun 2019;10:1843.
35. Cai Z, Zhu C, Wang X, Li L. Phase-field modeling of the coupled domain structure and dielectric breakdown evolution in a ferroelectric single crystal. Phys Chem Chem Phys 2019;21:16207-12.
36. Wang JJ, Wang B, Chen LQ. Understanding, predicting, and designing ferroelectric domain structures and switching guided by the phase-field method. Annu Rev Mater Res 2019;49:127-52.
37. Kim J, Saremi S, Acharya M, et al. Ultrahigh capacitive energy density in ion-bombarded relaxor ferroelectric films. Science 2020;369:81-4.
38. Zhao Y, Ouyang J, Wang K, et al. Achieving an ultra-high capacitive energy density in ferroelectric films consisting of superfine columnar nanograins. Energy Stor Mater 2021;39:81-8.
39. Xie J, Liu H, Yao Z, et al. Achieving ultrahigh energy storage performance in bismuth magnesium titanate film capacitors via amorphous-structure engineering. J Mater Chem C Mater 2019;7:13632-9.
40. Otoničar M, Bradeško A, Fulanović L, et al. Connecting the multiscale structure with macroscopic response of relaxor ferroelectrics. Adv Funct Mater 2020;30:2006823.
41. Yang Z, Gao F, Du H, et al. Grain size engineered lead-free ceramics with both large energy storage density and ultrahigh mechanical properties. Nano Energy 2019;58:768-77.
42. Yuan Q, Li G, Yao FZ, et al. Simultaneously achieved temperature-insensitive high energy density and efficiency in domain engineered BaTiO3-Bi(Mg0.5Zr0.5)O3 lead-free relaxor ferroelectrics. Nano Energy 2018;52:203-10.
43. Wang G, Li J, Zhang X, et al. Ultrahigh energy storage density lead-free multilayers by controlled electrical homogeneity. Energy Environ Sci 2019;12:582-8.
44. Zhao P, Cai Z, Chen L, et al. Ultra-high energy storage performance in lead-free multilayer ceramic capacitors via a multiscale optimization strategy. Energy Environ Sci 2020;13:4882-90.
45. Morozovska AN, Eliseev EA, Fomichov YM, et al. Controlling the domain structure of ferroelectric nanoparticles using tunable shells. Acta Mater 2020;183:36-50.
46. Yan F, Bai H, Shi Y, et al. Sandwich structured lead-free ceramics based on Bi0.5Na0.5TiO3 for high energy storage. Chem Eng J 2021;425:130669.
47. Wu L, Cai Z, Zhu C, Feng P, Li L, Wang X. Significantly enhanced dielectric breakdown strength of ferroelectric energy-storage ceramics via grain size uniformity control: Phase-field simulation and experimental realization. Appl Phys Lett 2020;117:212902.
48. Zhu D, Mangeri J, Wang R, Nakhmanson S. Size, shape, and orientation dependence of the field-induced behavior in ferroelectric nanoparticles. J Appl Phys 2019;125:134102.
49. Wang K, Ouyang J, Wuttig M, et al. Superparaelectric (Ba0.95,Sr0.05)(Zr0.2,Ti0.8)O3 ultracapacitors. Adv Energy Mater 2020;10:2001778.
50. Kwon O, Seol D, Lee D, et al. Direct probing of polarization charge at nanoscale level. Adv Mater 2018;30:1703675.
51. Dittmer R, Jo W, Rdel J, Kalinin S, Balke N. Nanoscale insight into lead-free BNT-BT-xKNN. Adv Funct Mater 2012;22:4208-15.
52. Wei Y, Wang X, Zhu J, Wang X, Damjanovic D. Dielectric, ferroelectric, and piezoelectric properties of BiFeO3-BaTiO3 ceramics. J Am Ceram Soc 2013;96:3163-8.
53. Sharma S, Singh V, Dwivedi RK. Electrical properties of (1-x) BFO-(x) PZT multiferroics synthesized by sol-gel method: transition from relaxor to non-relaxor. J Alloys Compd 2016;682:723-9.
54. Pan H, Zeng Y, Shen Y, et al. BiFeO3-SrTiO3 thin film as a new lead-free relaxor-ferroelectric capacitor with ultrahigh energy storage performance. J Mater Chem A 2017;5:5920-6.
55. Zhou M, Liang R, Zhou Z, Dong X. Novel BaTiO3-based lead-free ceramic capacitors featuring high energy storage density, high power density, and excellent stability. J Mater Chem C 2018;6:8528-37.
56. Wang J, Shi SQ, Chen LQ, Li Y, Zhang TY. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta Mater 2004;52:749-64.
57. Wang J, Ma X, Li Q, Britson J, Chen LQ. Phase transitions and domain structures of ferroelectric nanoparticles: phase field model incorporating strong elastic and dielectric inhomogeneity. Acta Mater 2013;61:7591-603.
58. Pan H, Li F, Liu Y, et al. Ultrahigh-energy density lead-free dielectric films via polymorphic nanodomain design. Science 2019;365:578-82.
59. Wang JJ, Su YJ, Wang B, Ouyang J, Ren YH, Chen LQ. Strain engineering of dischargeable energy density of ferroelectric thin-film capacitors. Nano Energy 2020;72:104665.
60. Tunkasiri T, Rujijanagul G. Dielectric strength of fine grained barium titanate ceramics. J Mater Sci Lett 1996;15:1767-9.
61. Cai Z, Wang X, Hong W, Luo B, Zhao Q, Li L. Grain-size-dependent dielectric properties in nanograin ferroelectrics. J Am Ceram Soc 2018;101:5487-96.
63. Chaitanya Pitike K, Hong W. Phase-field model for dielectric breakdown in solids. J Appl Phys 2014;115:044101.
64. Niemeyer L, Pietronero L, Wiesmann HJ. Fractal dimension of dielectric breakdown. Phys Rev Lett 1984;52:1033.
65. Sparks M, Mills D, Warren R, et al. Theory of electron-avalanche breakdown in solids. Phys Rev B 1981;24:3519.
66. Liu M, Cao M, Zeng F, et al. Fine-grained silica-coated barium strontium titanate ceramics with high energy storage. Ceram Int 2018;44:20239-44.
67. Li C, Yao M, Gao W, Yao X. High breakdown strength and energy density in antiferroelectric PLZST ceramics with Al2O3 buffer. Ceram Int 2020;46:722-73.
68. Wu L, Wang X, Li L. Enhanced energy density in core-shell ferroelectric ceramics: modeling and practical conclusions. J Am Ceram Soc 2016;99:930-7.
69. Yuan Q, Yao FZ, Cheng SD, et al. Bioinspired hierarchically structured all-inorganic nanocomposites with significantly improved capacitive performance. Adv Funct Mater 2020;30:2000191.
70. Shindo Y, Yoshida M, Narita F, Horiguchi K. Electroelastic field concentrations ahead of electrodes in multilayer piezoelectric actuators: experiment and finite element simulation. J Mech Phys Solids 2004;52:1109-24.
71. Li F, Jin L, Xu Z, Zhang S. Electrostrictive effect in ferroelectrics: an alternative approach to improve piezoelectricity. Appl Phys Rev 2014;1:011103.
72. Li J, Shen Z, Chen X, et al. Grain-orientation-engineered multilayer ceramic capacitors for energy storage applications. Nat Mater 2020;19:999-1005.
73. Lv P, Yang C, Qian J, et al. Flexible lead-free perovskite oxide multilayer film capacitor based on (Na0.8K0.2)0.5Bi0.5TiO3/Ba0.5Sr0.5(Ti0.97Mn0.03)O3 for high-performance dielectric energy storage. Adv Energy Mater 2020;10:1904229.
74. Sun Z, Wang L, Liu M, et al. Interface thickness optimization of lead-free oxide multilayer capacitors for high-performance energy storage. J Mater Chem A 2018;6:1858-64.
75. Wang Y, Chen J, Li Y, Niu Y, Wang Q, Wang H. Multilayered hierarchical polymer composites for high energydensity capacitors. J Mater Chem A 2019;7:2965-80.
76. Sun Z, Ma C, Liu M, et al. Ultrahigh energy storage performance of lead-free oxide multilayer film capacitors via interface engineering. Adv Mater 2017;29:1604427.
77. Fan Q, Liu M, Ma C, et al. Significantly enhanced energy storage density with superior thermal stability by optimizing Ba (Zr0.15Ti0.85)O3/Ba(Zr0.35Ti0.65)O3 multilayer structure. Nano Energy 2018;51:539-45.
78. Liu Y, Zhang B, Xu W, et al. Chirality-induced relaxor properties in ferroelectric polymers. Nat Mater 2020;19:1169-74.
79. Cheng ZY, Zhang Q, Bateman FB. Dielectric relaxation behavior and its relation to microstructure in relaxor ferroelectric polymers: high-energy electron irradiated poly (vinylidene fluoride-trifluoroethylene) copolymers. J Appl Phys 2002;92:6749.
80. Chen X, Tseng JK, Treufeld I, et al. Enhanced dielectric properties due to space charge-induced interfacial polarization in multilayer polymer films. J Mater Chem C 2017;5:10417-26.
81. Huang Y, Rui G, Li Q, et al. Enhanced piezoelectricity from highly polarizable oriented amorphous fractions in biaxially oriented poly (vinylidene fluoride) with pure β crystals. Nat Commun 2021;12:675.
82. Guo M, Guo C, Han J, et al. Toroidal polar topology in strained ferroelectric polymer. Science 2021;371:1050-6.
83. Meng N, Ren X, Santagiuliana G, et al. Ultrahigh β-phase content poly (vinylidene fluoride) with relaxor-like ferroelectricity for high energy density capacitors. Nat Commun 2019;10:4535.
84. Zhan C, Lian C, Zhang Y, et al. Computational insights into materials and interfaces for capacitive energy storage. Adv Sci 2017;4:1700059.
85. Schadler LS, Chen W, Brinson LC, et al. A perspective on the data-driven design of polymer nanodielectrics. J Phys D Appl Phys 2020;53:333001.
86. Sharma V, Wang C, Lorenzini RG, et al. Rational design of all organic polymer dielectrics. Nat Commun 2014;5:4845.
87. Ma R, Baldwin AF, Wang C, et al. Rationally designed polyimides for high-energy density capacitor applications. ACS Appl Mater Interfaces 2014;6:10445-51.
88. Ma R, Sharma V, Baldwin AF, et al. Rational design and synthesis of polythioureas as capacitor dielectrics. J Mater Chem A 2015;3:14845-52.
89. Sun Y, Boggs S, Ramprasad R. The intrinsic electrical breakdown strength of insulators from first principles. Appl Phys Lett 2012;101:132906.
90. Wang C, Pilania G, Boggs S, Kumar S, Breneman C, Ramprasad R, et al. Computational strategies for polymer dielectrics design. Polymer 2014;55:979-88.
91. Thakur Y, Zhang B, Dong R, et al. Generating high dielectric constant blends from lower dielectric constant dipolar polymers using nanostructure engineering. Nano Energy 2017;32:73-9.
92. Yuan C, Zhou Y, Zhu Y, et al. Polymer/molecular semiconductor all-organic composites for high-temperature dielectric energy storage. Nat Commun 2020;11:3919.
93. Luo B, Wang X, Wang H, Cai Z, Li L. P(VDF-HFP)/PMMA flexible composite films with enhanced energy storage density and efficiency. Compos Sci Technol 2017;151:94-103.
94. Zhang X, Shen Y, Shen Z, Jiang J, Chen L, Nan CW. Achieving high energy density in PVDF-based polymer blends: suppression of early polarization saturation and enhancement of breakdown strength. ACS Appl Mater Interfaces 2016;8:27236-42.
95. Zhang X, Jiang Y, Gao R, et al. Tuning ferroelectricity of polymer blends for flexible electrical energy storage applications. Sci China Mater 2021;64:1642-52.
96. Qian X, Ye HJ, Yang T, et al. Internal biasing in relaxor ferroelectric polymer to enhance the electrocaloric effect. Adv Funct Mater 2015;25:5134-9.
97. Jiang J, Shen Z, Qian J, et al. Ultrahigh discharge efficiency in multilayered polymer nanocomposites of high energy density. Energy Stor Mater 2019;18:213-21.
98. Zhang T, Dan Z, Shen Z, et al. An alternating multilayer architecture boosts ultrahigh energy density and high discharge efficiency in polymer composites. RSC Adv 2020;10:5886-93.
99. Li Q, Cheng S. Polymer nanocomposites for high-energy-density capacitor dielectrics: Fundamentals and recent progress. IEEE Electr Insul Mag 2020;36:7-28.
100. Zhu L, Wang Q. Novel ferroelectric polymers for high energy density and low loss dielectrics. Macromolecules 2012;45:2937-54.
101. Claude J, Lu Y, Li K, Wang Q. Electrical storage in poly (vinylidene fluoride) based ferroelectric polymers: correlating polymer structure to electrical breakdown strength. Chem Mater 2008;20:2078-80.
102. Tan DQ. The search for enhanced dielectric strength of polymer-based dielectrics: a focused review on polymer nanocomposites. J Appl Polym Sci 2020;137:49379.
103. Kim P, Jones SC, Hotchkiss PJ, et al. Phosphonic acid-modified barium titanate polymer nanocomposites with high permittivity and dielectric strength. Adv Mater 2007;19:1001-5.
104. Xie B, Zhu Y, Marwat MA, Zhang S, Zhang L, Zhang H. Tailoring the energy storage performance of polymer nanocomposites with aspect ratio optimized 1D nanofillers. J Mater Chem A 2018;6:20356-64.
105. Li J, Seok SI, Chu B, Dogan F, Zhang Q, Wang Q. Nanocomposites of ferroelectric polymers with TiO2 nanoparticles exhibiting significantly enhanced electrical energy density. Adv Mater 2009;21:217-21.
106. Zhang X, Chen W, Wang J, et al. Hierarchical interfaces induce high dielectric permittivity in nanocomposites containing TiO2@BaTiO3 nanofibers. Nanoscale 2014;6:6701-9.
107. Liu J, Shen Z, Xu W, et al. Interface-strengthened polymer nanocomposites with reduced dielectric relaxation exhibit high energy density at elevated temperatures utilizing a facile dual crosslinked network. Small 2020;16:2000714.
108. Wang P, Pan Z, Wang W, et al. Ultrahigh energy storage performance of a polymer-based nanocomposite via interface engineering. J Mater Chem A 2021;9:3530-9.
109. Zhang H, Marwat MA, Xie B, et al. Polymer matrix nanocomposites with 1D ceramic nanofillers for energy storage capacitor applications. ACS Appl Mater Interfaces 2019;12:1-37.
110. Zhang X, Jiang J, Shen Z, et al. Polymer nanocomposites with ultrahigh energy density and high discharge efficiency by modulating their nanostructures in three dimensions. Adv Mater 2018;30:1707269.
111. Bao Z, Hou C, Shen Z, et al. Negatively charged nanosheets significantly enhance the energy-storage capability of polymer-based nanocomposites. Adv Mater 2020;32:1907227.
112. Li H, Ai D, Ren L, et al. Scalable polymer nanocomposites with record high-temperature capacitive performance enabled by rationally designed nanostructured inorganic fillers. Adv Mater 2019;31:1900875.
113. Guo R, Roscow JI, Bowen CR, et al. Significantly enhanced permittivity and energy density in dielectric composites with aligned BaTiO3 lamellar structures. J Mater Chem A 2020;8:3135-44.
114. Zhou Y, Li Q, Dang B, et al. A scalable, high-throughput, and environmentally benign approach to polymer dielectrics exhibiting significantly improved capacitive performance at high temperatures. Adv Mater 2018;30:1805672.
115. Zhu Y, Zhu Y, Huang X, et al. High energy density polymer dielectrics interlayered by assembled boron nitride nanosheets. Adv Energy Mater 2019;9:1901826.
116. Shen ZH, Wang JJ, Jiang JY, et al. Phase-field model of electrothermal breakdown in flexible high-temperature nanocomposites under extreme conditions. Adv Energy Mater 2018;8:1800509.
117. Ma FD, Wang YU. Depolarization field effect on dielectric and piezoelectric properties of particulate ferroelectric ceramic-polymer composites. J Appl Phys 2015;117:124101.
118. Lewis TJ. Interfaces are the dominant feature of dielectrics at the nanometric level. IEEE Trans Dielectr Electr Insul 2004;11:739-53.
119. Roy M, Nelson J, MacCrone R, Schadler LS, Reed C, Keefe R. Polymer nanocomposite dielectrics-the role of the interface. IEEE Trans Dielectr Electr Insul 2005;12:629-43.
120. Tanaka T, Kozako M, Fuse N, Ohki Y. Proposal of a multi-core model for polymer nanocomposite dielectrics. IEEE Trans Dielectr Electr Insul 2005;12:669-81.
121. Shen ZH, Wang JJ, Zhang X, et al. Space charge effects on the dielectric response of polymer nanocomposites. Appl Phys Lett 2017;111:092901.
122. Pan Z, Zhai J, Shen B. Multilayer hierarchical interfaces with high energy density in polymer nanocomposites composed of BaTiO3@TiO2@Al2O3 nanofibers. J Mater Chem A 2017;5:15217-26.
123. Shen ZH, Shen Y, Cheng XX, Liu HX, Chen LQ, Nan CW. High-throughput data-driven interface design of high-energy-density polymer nanocomposites. J Materiomics 2020;6:573-81.
124. Shen ZH, Wang JJ, Lin Y, Nan CW, Chen LQ, Shen Y. High-throughput phase-field design of high-energy-density polymer nanocomposites. Adv Mater 2018;30:1704380.
125. Shen ZH, Bao ZW, Cheng XX, et al. Designing polymer nanocomposites with high energy density using machine learning. NPJ Comput Mater 2021;7:110.
126. Tang H, Lin Y, Sodano HA. Enhanced energy storage in nanocomposite capacitors through aligned PZT nanowires by uniaxial strain assembly. Adv Energy Mater 2012;2:469-76.
127. Luo S, Yu J, Yu S, et al. Significantly enhanced electrostatic energy storage performance of flexible polymer composites by introducing highly insulating-ferroelectric microhybrids as fillers. Adv Energy Mater 2019;9:1803204.
128. Fan L, Yang D, Huang L, Fan M, Lei C, Fu Q. Polymer nanocomposite with enhanced energy storage capacity by introducing hierarchically-designed 1-dimension hybrid nanofiller. Polymer 2020;201:122608.
129. Pan Z, Yao L, Zhai JW, Fu D, Shen B, Wang H. High-energy-density polymer nanocomposites composed of newly structured one-dimensional BaTiO3@Al2O3 nanofibers. ACS Appl Mater Interfaces 2017;9:4024-33.
130. Luo B, Shen Z, Cai Z, et al. Superhierarchical inorganic/organic nanocomposites exhibiting simultaneous ultrahigh dielectric energy density and high efficiency. Adv Funct Mater 2021;31:2007994.
131. Jiang J, Shen Z, Cai X, et al. Polymer nanocomposites with interpenetrating gradient structure exhibiting ultrahigh discharge efficiency and energy density. Adv Energy Mater 2019;9:1803411.
132. Azizi A, Gadinski MR, Li Q, et al. High-performance polymers sandwiched with chemical vapor deposited hexagonal boron nitrides as scalable high-temperature dielectric materials. Adv Mater 2017;29:1701864.
133. Wang Y, Cui J, Yuan Q, Niu Y, Bai Y, Wang H. Significantly enhanced breakdown strength and energy density in sandwich-structured barium titanate/poly (vinylidene fluoride) nanocomposites. Adv Mater 2015;27:6658-63.
Cite This Article
Open AccessHow to Cite
Wang, J.; Shen Z. H. Modeling-guided understanding microstructure effects in energy storage dielectrics. Microstructures. 2021, 1, 2021006. http://dx.doi.org/10.20517/microstructures.2021.05
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
About This Article
Copyright
Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.