Neural network to predict 23Na NMR spectra of Nan clusters
Abstract
In order to understand the charging and discharging processes of sodium-ion batteries, we are interested in the relationship between the size of sodium clusters inserted into the hard carbon anode and the solid-state 23Na NMR chemical shifts. In this study, we investigated the predictability of the size dependence of 23Na NMR shielding constants by SchNet, a deep learning model that uses the distance between Na atoms without graph connection information. The data set required for training the neural network was constructed by density functional theory (DFT) calculations. This study shows that the neural network model, which only used structural data, achieved comparable accuracy in predicting the shielding constant to the Lasso model, which utilized gross orbital population predicted from DFT calculations. Moreover, by introducing a penalty term to the neural network's loss function, the neural network was able to reproduce the skewed distribution of the shielding constant without modifying its architecture.
Keywords
INTRODUCTION
Lithium-ion batteries (LIBs) are essential and used in various devices. The demand for rechargeable batteries is expected to increase as electric vehicles become common nowadays; however, owing to the risk of instability in the supply of raw materials, it is crucial to develop battery technologies that can be applied as an alternative to LIBs.
The abundance of sodium in the earth’s crust is 23,600 ppm, which is significantly higher than that of lithium (20 ppm)[1], making sodium-ion batteries (SIBs) an attractive alternative to LIBs. Hard carbon (HC) exhibits potential for application in the SIB anode. The charge-discharge process needs to be further explored[2,3]. Therefore, we used nuclear magnetic resonance (NMR) spectroscopy, one of the primary techniques to obtain information on the molecular structure of compounds, to improve the performance of HC anodes. The effect of HC preparation conditions on the amount of sodium inserted into HC anodes using solid 23Na NMR chemical shifts has been experimentally analyzed[2-4]. The correlation of NMR chemical shifts of sodium clusters based on pore size and structure is a relevant technique to evaluate the size distribution of closed pores in HCs and other amorphous carbon materials. However, with regard to the computational cost, it becomes difficult to predict NMR chemical shifts of large sodium clusters based on the density functional theory (DFT).
In recent years, graph convolutional networks (GCNs) have been developed to predict the physical properties of various molecules by considering the atomic information on the vicinity of the bond based on convolution[4]. For example, NMR chemical shifts of small molecules, e.g., 1H and 13C, can be predicted using the message passing neural network, which is an enhanced version of the GCN model[5]. However, it is difficult to use the model that utilizes graphical information for sodium clusters since the graph information is not sufficient for them. On the contrary, SchNet[6,7] proposed by Schütt et al., is a deep learning model that uses the distance between atoms instead of the connection information of the graph.
This study investigates the possibility of using SchNet to predict the shielding constant of 23Na NMR based on the structure of sodium clusters. First, a baseline model is created to verify the performance of the SchNet neural network model using Lasso regression, in which coordination numbers are learned as structural descriptors. The results of the DFT calculations are added to the coordination numbers as descriptors of the gross population to train the Lasso regression. Although SchNet has generally been used to predict molecular energies and forces on nuclei, formally, it can also be adapted to cluster models. Therefore, in this study, we use SchNet to create a model that predicts NMR shielding constants from the structure of Na clusters and evaluate the performance of this model by comparing it to Lasso regression.
MACHINE LEARNING
Data set
The second-order bond length distribution algorithm (S-BLDA)[8], an algorithm based on bond length distribution analysis, was used to generate random Nan (n = 14, 16, ..., 28, 30, 40) cluster structures. Parameters of S-BLDA were set to μ1 = 3.50 Å, μ2 = 3.60 Å, and σ1 = σ2 = 0.1 Å. S-BLDA creates clusters by adding one atom to the current structure each time. Atoms are added so that the distribution of the distance between each atom and its neighbors and the distribution of the distance between each atom and its next neighbor can approximate a normal distribution (mean μ1, standard deviation σ1) and a normal distribution (mean μ2, standard deviation σ2), respectively. These parameters were determined to reproduce the distribution of distances between atoms in the clusters that were structurally optimized by DFT calculations.
The NMR isotropic shielding constant σiso for the generated structures was determined based on DFT calculations using Gaussian16[9]. B3LYP[10,11] and 6-31G(d) were used for a functional and a basis function, respectively. The electronic wavefunction was described by an open-shell singlet state, and structures with eigenvalues of the spin operator S2 less than 0.05 were used to avoid spin contamination, and the structure generation was repeated until 200 structures were obtained for each n. Nan (n = 14, 16, ..., 26), Nan (n = 28, 30), and Nan (n = 40) were used as the training, validation, and test sets. The neural network was trained to minimize the loss function of the validation set.
Lasso regression
With the atomic shielding constant as the objective variable[12], Lasso regression was used. The running coordination number and/or gross orbital population were used as the explanatory variables. The running coordination number is the number of atoms located from the center of an atom to the radius rmax. The delta function used to calculate the running coordination number is approximated by a normally distributed density function with σ = 0.01 Å. Therefore, the running coordination number can be a fraction. The values used for rmax were rmax = 3.1, 3.2, ..., 12.0 Å. These explanatory variables are highly correlated, and we expect that the use of Lasso regression will improve model stability and robustness by automatically performing feature selection, providing a sparse representation of the model and preventing over-training and multicollinearity.
The functions, 1S, 2S, 2PX, 2PY, 2PZ, 3S, 3PX, 3PY, 3PZ, 4S, 4PX, 4PY, 4PZ, 5DXX, 5DYY, 5DZZ, 5DXY, 5DXZ, and 5DYZ, in the 6-31G(d) basis were used as the gross orbital population. The explanatory variables were standardized such that the mean value of the shielding constant of the training set and the variance were 0 and 1, respectively. The α parameters of Lasso regression were each fitted to the training set with a model that had α = 10-5, 10-4,...,104, 105 and selected to minimize the RMSE against the validation set.
Neural network
SchNet, as implemented in SchNetPack 1.0.0[13], was used. It predicts the properties of molecules by combining the contributions of individual atoms; however, instead of combining contributions, this study uses the value of the contribution of each atom to predict the value of the atomic shielding constant. The “Number of features to describe atomic environments”, “Number of filters used in continuous-filter convolution”, and “Number of Gaussian functions used to expand atomic distance” were set to SchNet default values of 128, 128, and 25, respectively. The “Number of interaction blocks” and “Cutoff radii” were 2 and 6.0 Å, respectively. Shifted Softplus was used as the activation function for hidden NNs, and Adam optimizer[14] was used at a learning rate of 0.01. The mini-batch size was set to 100. A maximum of 2,000 epochs of training was carried out. As results significantly depend on the initial weights of the neural network, twenty different seeds to generate pseudo-random numbers were used, and the model with the best performance against validation was selected.
Loss function
Shielding constants exhibited a generalized logistic distribution irrespective of the number of atoms in the clusters [Figure 1]. As this distribution is skewed to the left, if neural networks were trained with the mean squared error (MSE) as a loss function, the neural networks would focus on low values and neglect values around the most frequent value. Therefore, the shielding constant was used for the cumulative distribution function (CDF) of the generalized logistic distribution and the percent point function of the standard normal distribution. In other words, the probability distribution was transformed by adapting the inverse CDF of the standard normal distribution to the CDF of the generalized logistic distribution.
Figure 1. Distribution of the shielding constant σiso for cluster size n and the fitting curve of the generalized logistic distribution.
The generalized logistic distribution used parameters fitted to the distribution of shielding constants in the training set.
The loss function was set as follows, with a term added to the MSE to reproduce the distribution.
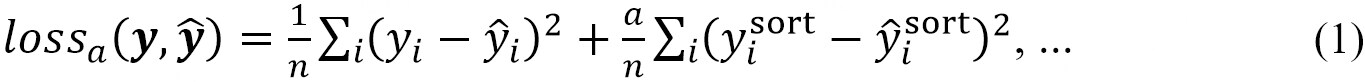
where y is the shielding constant calculated using the DFT and 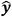 is the shielding constant predicted by the neural network,
is the shielding constant predicted by the neural network, 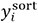 . In addition,
. In addition, 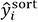 are the values of shielding constants sorted in the mini-batch. In this study, a = 3 was used.
are the values of shielding constants sorted in the mini-batch. In this study, a = 3 was used.
In order to reproduce the shape of the distribution, it is necessary to output values corresponding to the tails of the distribution. However, since it is difficult to predict these values accurately, the predicted values for some samples may have large errors, which may worsen the RMSE. Additionally, when minimizing RMSE, samples that show values at the base of the distribution tend to be less important because they are few relative to other samples. Thus, there is a trade-off between reproducing the shape of the distribution and RMSE.
RESULTS AND DISCUSSION
Lasso regression
We confirmed the relationship between the shielding constant and the gross orbital population. Regarding relations to the shielding constant, 3S was positively correlated, and 3P was negatively correlated [Figure 2A and B]. In contrast, 4S, which constitutes the 3s orbital, and 4P, which constitutes the 3p orbital, as well as 3S and 3P, show no correlation with the shielding constant [Figure 2C and D]. Based on the relation between the coordination number and the gross orbital population [Figure 2E and F], when the coordination number is small, only 3S orbitals are found. When the coordination number starts to increase, the number of 3S orbitals decreases while that of 3P increases. However, when the coordination number increases further, the number of 3S starts to increase as well. In other words, the atoms near the surface have mainly 3S orbitals with high shielding constants; the interior atoms have both 3S and 3P orbitals with large shielding constants, and the atoms in between the coordination numbers tend to have 3P orbitals with smaller shielding constants.
Figure 2. Relation between the gross orbital population (GOP). (A) 3S; (B) 3PX; (C) 4S; and (D) 4PX and the shielding constant, and the relation between the coordination number (rmax = 4.0 Å) and GOP; (E) 3S and (F) 3PX.
We predicted the shielding constant using Lasso regression with the coordination number and gross orbital population as the explanatory variables [Figure 3]. The RMSE was 37.6 ppm when using the coordination number [Figure 3A], and it was 35.1 ppm when using the gross orbital population [Figure 3C]. As the NMR shielding constant is strongly influenced by the electrons in the s orbitals, it is assumed that these results reflect that the gross orbital population is effective in predicting the shielding constant. However, the coordination number can be calculated only from the structure, whereas the gross orbital population can be obtained only using DFT calculation. The RMSE of the model using these two types of explanatory variables simultaneously was 34.9 ppm, which hardly differed from that using the gross orbital population alone. Next, by transforming the shielding constant to a normal distribution, the peak position shifted to the right and approached the distribution peak provided by the DFT analysis. However, the RMSE deteriorated considerably. It is assumed that this is because the machine learning model learns to minimize the error in the shielding constant after the conversion by converting the shielding constant to a normal distribution.
Figure 3. Distribution of the shielding constants predicted by Lasso, and scatter plots of the shielding constants predicted by Lasso vs. those calculated by DFT for the test set Na40. To handle shielding constants that follow a generalized logistic distribution, in (B) and (D), the shielding constants are once transformed to a normal distribution to train the Lasso model. When making predictions, the prediction values of the Lasso model were back-transformed into shielding constants based on the original generalized logistic distribution. On the other hand, in (A) and (C), the shielding constants are predicted directly. In terms of the explanatory variables, (A) and (B) use the coordination numbers calculated from the structure, and (C) and (D) use the gross orbital population calculated by DFT calculations.
From the analysis of the gross orbital population, the atoms near the surface have mainly 3S orbitals with high shielding constants, and the atoms in the interior have both 3S and 3P orbitals with large shielding constants; the atoms with coordination numbers in between tend to have 3P orbitals with small shielding constants.
Neural network
The neural network was trained, and its prediction performance was verified for the test set. First, the distribution of shielding constants calculated using the DFT for the test set Na40 [Figure 4A] peaks around 600 ppm, which is similar to a generalized logistic distribution as illustrated by the Quantile-Quantile plot (Q-Q plot) [Figure 4B].
Figure 4. Q-Q plot for (A) the distribution of shielding constants and (B) generalized logistic distribution for the test set Na40.
The predicted values of the neural network were compared with the DFT-calculated values [Figure 5]. The model trained with MSE as a loss function [Figure 5A and C] reproduced the average value but failed to output the most frequent value and shielding constant below 500 ppm. On the contrary, the loss function of Equation (1), introduced in this study [Figure 5B and D], deteriorated the root mean square error (RMSE); however, it reproduced the shape of the distribution of the shielding constant, and the position of the peak shifted to the right. No significant change was observed in the distribution of the predicted values when the shielding constant was converted to generate a normal distribution.
Figure 5. Distribution of shielding constants predicted by the neural network and the scatter plot of the shielding constants predicted by the neural network vs. the shielding constant calculated using the DFT based on the test set Na40. Two approaches were employed for handling the generalized logistic distribution of shielding constants. One approach is to convert the shielding constant to a normal distribution before training the neural network in (C) and (D). However, before plotting, the neural network predictions are converted to the original generalized logistic distribution. In contrast, in (A) and (B), the shielding constants are learned directly. The other approach used Equation (1) as the loss function in (B) and (D). In contrast, (A) and (C) employ only MSE as the loss function.
There were issues in both the Lasso regression and neural network models, as the peaks in the distribution of the predicted shielding constant did not coincide with those given by DFT. Therefore, the shielding constants were converted to a normal distribution, and the shielding constants were predicted after the conversion. As a result, in the Lasso regression model, the peak position shifted to the right and approached the distribution peak given by DFT. However, the peak position did not shift in the neural network model, showing that it had no effect.
Figure 3A and B predict shielding constants by Lasso regression using only the simplest descriptor, coordination numbers. Figure 5A-D uses SchNet to predict shielding constants from information on more complex structures. Comparing these results, the RMSE of Figure 5A and C is smaller than that of the Lasso regression, indicating that the prediction performance is improved. Moreover, Figure 3C has the smallest RMSE in this case. This is due to the use of the gross orbital population from the DFT calculation as the descriptor. However, SchNet, which predicts shielding constants from structural information alone without using the results of DFT calculations, succeeded in predicting RMSE comparable to the smallest RMSE
The large RMSE of these neural networks is expected to be caused by the difficulty in predicting shielding constants for low values, i.e., below 500 ppm. The relationship between the shielding constants and running coordination number at a radius of 4.0 Å indicates that such low values of shielding constants are obtained for Na atoms with intermediate coordination numbers ranging from 4 to 9 [Figure 6]. The running coordination number represents the number of Na atoms located at radius rmax from the center of a Na atom as the delta function used in the calculation is approximated using a normally distributed density function with σ = 0.01 Å, the running coordination number can be small.
Figure 6. Relationship between the shielding constant and running coordination number at a radius of 4.0 Å for the entire data set.
Structures of Na20 clusters optimized by Murrell–Mottram potential [Figure 7A][15] and the particle swarm optimization (CALYPSO) method[16] have been reported, both possessing a Na atom with coordination number 12 in the center. However, structures generated using the proposed method rarely exhibit high coordination numbers [Figure 6]. Such an unstable cluster structure reduces the shielding constant, i.e., below 500 ppm. To solve this problem, the neural network can be trained using stable cluster structures as data are obtained using structural optimization.
Figure 7. Line plot of the structure of Na20 and the running coordination number of each atom (represented by a different colored line) in the structure. (A) Stable structure predicted based on Murrell-Mottram potential[15]; (B) structure generated in this study; (C) structure-optimized version of (B). (A) and (B) are outlier atoms with shielding constants of 368.1 and 386.4 ppm, respectively.
One cluster structure, which includes outliers, is extracted and analyzed. The cluster structures and their running coordination numbers are shown in Figure 7B, where Na atoms with shielding constants of 368.1 and 386.4 ppm are located in the range of 4-7. The cluster structures appear to include 9-10 coordinated Na atoms at most. The optimized cluster structure is shown in Figure 7C. The cluster structure is round (almost spherical), and one Na atom exhibits a coordination number of 12. The minimum value of the shielding constant of the cluster structure is 581.9 ppm, which indicates that the cluster structure does not include any Na atoms with a shielding constant outlier. Thus, the number of shielding constant outliers can be reduced using structural optimization. The reason for the wider hem in Figure 1 can be attributed to the fact that the clusters have not undergone structural optimization calculations.
If the neural network is trained based on the cluster structure, which was structurally optimized based on the DFT level, this neural network for unknown structures is required to calculate the DFT level every time. Therefore, structural optimization using the self-consistent-charge density-functional tight-binding method[17,18], which incurs a low cost, can help reduce computational costs. DFTB is effective in generating structures for gold and silver clusters[19]. Moreover, Gupta potential[15,20,21] or Murrell-Mottram potential[15], which have been globally used to optimize Na clusters, can be an alternative. The CALYPSO method has successfully explored the structures of medium-sized metal-doped boron clusters[22-25] and silicon clusters[26].
CONCLUSION
This study used a SchNet-based neural network to predict shielding constants of Na clusters and structures generated using the S-BLDA method.
The RMSE of the model using the neural network was 35.2 ppm, which was almost the same as the 34.9 and 35.1 ppm obtained in the Lasso regression model that respectively used the running coordination number and gross orbital population, or only the gross orbital population as the explanatory variables. While the neural network model used only the structure data, the Lasso regression model used the gross orbital population predicted by the DFT calculation as an explanatory variable. Therefore, it is considered that this neural network model, using only the structure data, achieved comparable performance to that of the Lasso model, which uses gross orbital population correlated with the shielding constant.
The S-BLDA method exhibited a skewed distribution for shielding constants, yielding low shielding constants. This may be because the randomly generated non-equilibrium cluster structure tends to destabilize electronic states, resulting in unrealistic values of the shielding constant, which are extremely low. SchNet and Lasso were unable to reproduce such a distribution. However, by adding a penalty term to reproduce the original distribution as a loss function, the distorted distribution can be handled without changing the structure of the neural network. It became possible to output an extremely low shielding constant.
To further improve the prediction performance, it would be necessary to stabilize each structure to reduce the anomalies in the shielding constants and improve the performance of each system. Future research will be conducted in this direction.
DECLARATIONS
AcknowledgmentsYamashita K acknowledges the support from Toyota Physical and Chemical Research Institute. Computations were performed at the Research Center for Computational Science, Okazaki, Japan.
Authors’ contributionsPerformed machine learning modeling and data analysis as well as draft writing: Kaneko M
Performed quantum chemical calculations: Suzaki A
Made contributions to the discussion from the perspective of quantum chemical calculations: Muraoka A
Made contributions to the discussion from an experimental point of view: Gotoh K
Supervised the research: Yamashita K
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was supported by the Elements Strategy Initiative for Catalysts and Batteries (ESICB) at Kyoto University.
Conflict of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2023.
REFERENCES
1. Yabuuchi N, Kubota K, Dahbi M, Komaba S. Research development on sodium-ion batteries. Chem Rev 2014;114:11636-82.
2. Morita R, Gotoh K, Kubota K, et al. Correlation of carbonization condition with metallic property of sodium clusters formed in hard carbon studied using 23Na nuclear magnetic resonance. Carbon 2019;145:712-5.
3. Morita R, Gotoh K, Fukunishi M, et al. Combination of solid state NMR and DFT calculation to elucidate the state of sodium in hard carbon electrodes. J Mater Chem A 2016;4:13183-93.
4. Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv 2016:1609.02907.
5. Kwon Y, Lee D, Choi YS, Kang M, Kang S. Neural message passing for NMR chemical shift prediction. J Chem Inf Model 2020;60:2024-30.
6. Schütt KT, Arbabzadah F, Chmiela S, Müller KR, Tkatchenko A. Quantum-chemical insights from deep tensor neural networks. Nat Commun 2017;8:13890.
7. Schütt KT, Sauceda HE, Kindermans PJ, Tkatchenko A, Müller KR. SchNet - a deep learning architecture for molecules and materials. J Chem Phys 2018;148:241722.
8. Zhai H, Alexandrova AN. Ensemble-average representation of pt clusters in conditions of catalysis accessed through GPU accelerated deep neural network fitting global optimization. J Chem Theory Comput 2016;12:6213-26.
9. Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian 16. Gaussian Inc.: Wallingford, USA; 2016.
10. Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B Condens Matter 1988;37:785-9.
11. Zhao Y, Schultz NE, Truhlar DG. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions. J Chem Theory Comput 2006;2:364-82.
12. Santosa F, Symes WW. Linear inversion of band-limited reflection seismograms. SIAM J Sci Stat Comput 1986;7:1307-30.
13. Schütt KT, Kessel P, Gastegger M, Nicoli KA, Tkatchenko A, Müller KR. SchNetPack: a deep learning toolbox for atomistic systems. J Chem Theory Comput 2019;15:448-55.
14. Kingma DP, Ba J. Adam: a method for stochastic optimization. arXiv preprint arXiv ;2014:1412.6980.
15. Noya EG, Doye JP, Wales DJ, Aguado A. Geometric magic numbers of sodium clusters: Interpretation of the melting behaviour. Eur Phys J D 2007;43:57-60.
16. Sun WG, Wang JJ, Lu C, Xia XX, Kuang XY, Hermann A. Evolution of the structural and electronic properties of medium-sized sodium clusters: a honeycomb-like Na20 cluster. Inorg Chem 2017;56:1241-8.
17. Elstner M, Porezag D, Jungnickel G, et al. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys Rev B 1998;58:7260-8.
18. Frauenheim T, Seifert G, Elsterner M, et al. A self-consistent charge density-functional based tight-binding method for predictive materials simulations in physics, chemistry and biology. Physica Status Solidi 2000;217:41-62.
19. Oliveira LFL, Tarrat N, Cuny J, et al. Benchmarking density functional based tight-binding for silver and gold materials: from small clusters to bulk. J Phys Chem A 2016;120:8469-83.
21. Doye JP. Lead clusters: different potentials, different structures. Comput Mater Sci 2006;35:227-31.
22. Le Chen B, Sun WG, Kuang XY, et al. Structural stability and evolution of medium-sized tantalum-doped boron clusters: a half-sandwich-structured TaB12- cluster. Inorg Chem 2018;57:343-50.
23. Jin S, Chen B, Kuang X, et al. Structural and electronic properties of medium-sized aluminum-doped boron clusters AlB n and their anions. J Phys Chem C 2019;123:6276-83.
24. Sun W, Xia X, Lu C, Kuang X, Hermann A. Probing the structural and electronic properties of zirconium doped boron clusters: Zr distorted B12 ligand framework. Phys Chem Chem Phys 2018;20:23740-6.
25. Tian Y, Wei D, Jin Y, Barroso J, Lu C, Merino G. Exhaustive exploration of MgBn (n = 10-20) clusters and their anions. Phys Chem Chem Phys 2019;21:6935-41.
Cite This Article
How to Cite
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.

























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at [email protected].