Figure1

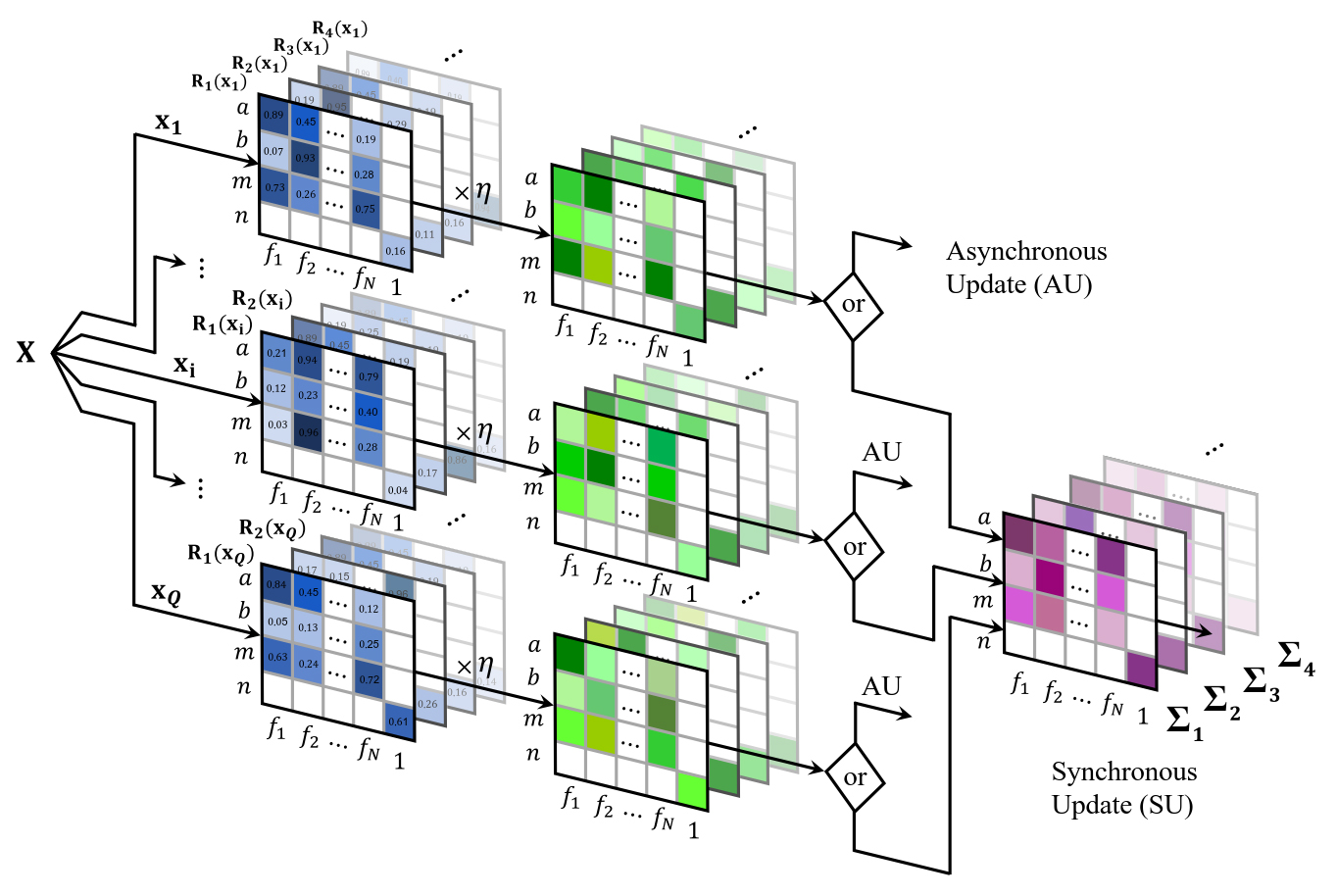
Figure 1. Synchronous and asynchronous approaches for the update of the system's parameters. Each observation of the dataset has a different set of matrices that together constitute the gradient of the loss function (transparent matrices of the back refer to different clusters). The entries of the blue matrices represent the derivatives with respect to the different parameters of the system; the rows determine the type of the parameter, $$ a $$, $$ b $$, $$ m $$, or $$ n $$, organized in a top-down fashion, and the columns identify the input feature (denoted with letter f, and 1 for the independent term). The green matrices are obtained after weighting the derivatives with the learning rates, which do not necessarily need to be identical for all the parameters. Finally, the resulting matrix could be added to those obtained for the other observations, creating the purple matrices, or it can be used before moving to the next instance of the training sample. The first approach is labeled as a synchronous update and considers a single update of the parameters in every epoch after all the observations have been visited. We identify the second approach as an asynchronous update, which requires, within the same epoch, as many updates of the parameters as observations are in the sample.